2. 1. 3. Нескінченно малі послідовності та їх властивості

В цьому параграфі ми починаємо вивчати ті послідовності, які дозволяють в майбутньому ввести основні поняття математичного аналізу.

Розглянемо такі послідовності,

1. 

2. 

3. 

4. 

Зобразимо члени цих послідовностей на числовій осі

a)

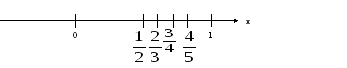
b)

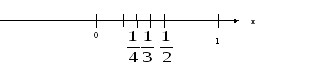
c)

d)

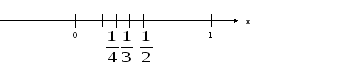
Аналізуючи послідовності a)-d) ми помічаємо, що лише одна із них – b), має властивість: який би ми окіл точки 0 не взяли, знайдеться номер починаючи з якого, всі члени послідовності належатимуть цьому околу. Послідовність а) такої властивості не має, бо взявшинемає жодного її члена, який би належав цьому околу. Послідовність d) також такої властивості не має, бо взявшибачимо що жодний її член теж не належить цьому околу. Що ж стосується послідовності с), то який би ми окіл не взяли не знайдетьсяпісля якого всі члени належали б цьому околу. „Бунтівниками” виступатимуть члени з парними номерами (звичайно якщо радіус околу ми будемо брати меншим за одиницю).

Після цього ми можемо дати наступне

Означення 1. Послідовність називаєтьсянескінченно малою, якщо

Як випливає з цього означення натуральне число залежить від виборуі напевно із зменшеннямне зменшується. Оскільки те, щорівносильне тому, щоабоа остання нерівність рівносильна такійто наше означення нескінченно малої послідовності можна записати ще й так.

Означення 1’. Послідовність називаєтьсянескінченно малою послідовністю, якщо

Покажемо, що наша послідовність b) є нескінченно малою. Це треба зробити, тому що ми перевірили виконання означення 1 і 1’ лише для кількох значень Нехайпро яке йде мова в означенніми знайдемо (якщо знайдемо!?) з нерівностірозв’язавши її. Будемо матиЯкщо через- позначимо найбільше ціле число, яке не перевищує числа(це числоназивається цілою частиною числа), то покладемоТепер, якщо взяти довільнетоі отжевходить до множини розв’язків нашої нерівності і тому при такихсправедлива нерівністьа це означає, що послідовність є нескінченно малою.

З’ясуємо чи можна здійснювати над нескінченно малими послідовностями арифметичні операції. Почнемо з такого твердження.

Теорема 1. Сума двох нескінченно малих послідовностей також буде нескінченно малою .

Доведення. Нехай і- нескінченно малі послідовності.

Візьмемо З того, що обидві ці послідовності нескінченно малі, згідно означення 1’ будемо мати:

для (1)

для (2)

Позначимо через максимальне з чиселіі розглянемо далі(для такихнерівності(1) і (2) виконуватимуться одночасно). Тоді матимемо, А це означає, що послідовністьє нескінченно малою. Теорема доведена.

Очевидно її можна узагальнити.

Теорема 1’. Сума - штук (довільної скінченої кількості) нескінченно малих послідовностей є зновунескінченно мала послідовність.

Неважко догадатись, дивлячись на доведення теореми 1, як довести наступний факт.

Теорема 2. Добуток двох нескінченно малих послідовностей є нескінченно малою послідовністю.

Що стосується різниці нескінченно малих послідовностей, то вона теж буде нескінченно малою, що доводиться так само як теорема 1, тільки у відповідному місці використовується нерівність:

Що стосується частки двох нескінченно малих послідовностей, то тут ситуація зовсім інша ніж в попередніх арифметичних діях. Наприклад, частка двох нескінченно малих послідовностей і деіприводить до послідовності 1,1,1,1,1,1,…, яка очевидно не є нескінченно малою.

Якщо ж взяти то- теж не є нескінченно малою. Проте, якщо взятито- вже є нескінченно малою послідовністю. Ці приклади показують, щочастка двох нескінченно малих послідовностей не зобов’язана бути нескінченно малою послідовністю.

Повернемось знов до добутку послідовностей. Справедлива

Теорема 3. Добуток нескінченно малої послідовності на обмежену є нескінченно малою послідовністю.

Доведення. Нехай - нескінченно мала послідовність, -обмежена послідовність. Останнє означає

(3)

Візьмемо далі Тоді з того, що послідовність нескінченно мала матимемо за означенням 1’,

для (4)

Тоді будемо мати

а це означає, що послідовність є нескінченно малою. Теорема доведена.

Що стосується добутку нескінченно малої на необмежену, то тут можливі ситуації. Пропонуємо читачу розібрати їх самостійно. Тепер ми вже можемо ввести одне із фундаментальних понять математичного аналізу.