2. Корисність за Нейманом. Сподівана корисність.

Для визначення корисності розглянемо вибір особи за умов ризику, який формалізується за допомогою поняття лотереї.

Для цього необхідно з множини пред’явлених експертам значень певного економічного показника (об’єкта) виділити два х_* и х^* таких, що х_*хдля всіх х_*Хта х^*хдля всіх хХ, тобто найменш пріоритетне, в певному сенсі, значення економічного показника (це буде «нуль» даної шкали інтервалів) і найбільш пріоритетне у певному сенсі значення показника (разом з «нулем» воно визначить масштаб даної шкали). Власне так побудована функція корисності Дж. Неймана і О. Моргенштерна. Експерту пропонують порівнювати альтернативу:

1) значення показника х;

2) лотерею: одержати х^* з імовірністю (1 - р) чи х_* з імовірністю (р). Величину імовірності р змінюють доти, доки, на погляд експерта, значення показника х і лотерея L (х^*, р, х_*) не стануть еквівалентними. Максимальному та мінімальному значенням х^* та х_* приписують довільні числові значення U^*= U(х^*) та U_*= U(x_*), але так, щоб U^* > U_*.

Пiд лотереєю L (х_*, р(х), х^*) розуміють ситуацію, в якій особа може отримати х_* з імовірністю р(х) або х^* з імовірністю 1 - р(х).

Корисність варіанту х визначається ймовірністю р(х), при якій особі байдуже, що обирати: х — гарантовано, чи лотерею L (х_*, р(х), х^*), де х^*, х_* — вектори, більш та менш пріоритетні порівняно з х.

Нехай L — лотерея, що призводить до виграшів (подій) х₁,х₂,....х_n з відповідними ймовірностями р₁, p₂, ….р_N. Позначимо сподіваний виграш (математичне сподівання виграшу) через х.

Справедлива головна формула теорії сподіваної корисності

тобто корисність ансамблю результатів збігається математичним сподіванням корисності результатів.

Поняття детермінованого еквівалента лотереї L є одним з основних при розгляді різних характеристик ризику і їх взаємозв'язку з функціями корисності.

Детермінований еквівалент лотереї L – це гарантована сума, отримання якої еквівалентне участі в лотереї, тобто ~ L. Отже визначається з рівняння:

U(x) = M [U(x)], або = U^-1MU(x)

Сподіваний виграш та детермінований еквівалент, які визначені згідно з наведеними формулами, стосуються лотереї з кінцевим числом можливих виграшів. Якщо можливі виграші описуються щільністю розподілу φ(х), то сподіваний виграш у цій лотереї дорівнює

а детермінований еквівалент є розв’язком рівняння:

Згідно з теорією сподіваної корисності, суб’єкт керування, що приймає рішення за умов невизначеності та ризику, повинен максимізувати математичне сподівання корисності результатів. Отже, якщо f(x, ω) – вектор результатів, що залежать від вектора плану х та елементарної події ω, то ефективність плану х для значень ω, які містяться у множині Ω, ω Ω з імовірнісною мірою Р(dω), має вид

Величина Р(dω) визначається або за статистичними методами при наявності необхідної кількості спостережень, або за допомогою спеціальних експертних процедур.

3. Різне ставлення до ризику та корисність.

Особу, яка приймає рішення, називають несхильною до ризику, якщо для неї більш пріоритетною є можливість отримати гарантовано сподіваний виграш у лотереї, ніж приймати в ній участь.

З попереднього відомо, що корисність лотереї збігається з математичним сподіванням корисності її випадкових результатів. Отже умова несхильності до ризику приймає вид

U (M [x (ω)]) > M [U (x (ω))],

де М( ) – символ (оператор) математичного сподівання, х – випадкова величина, що залежить від елементарної події ω.

Для зростаючих функцій корисності премією π(х) за ризик в лотереї L є різниця між сподіваним виграшем та детермінованим еквівалентом

π(х) = М [x (ω)] - .

Страховою сумою (СС) називають величину детермінованого еквіваленту з протилежним знаком, тобто

CC(x) = -= -U^-1 (M [U (x (ω))].

Умова схильності до ризику має вид

U (M [x (ω)]) < M [U (x (ω))].

Умова байдужості до ризику має вид

U (M [x (ω)]) = M [U (x (ω))].

Приклади функцій корисності:

1) зростаюча функція корисності для суб'єкта керування байдужого до ризику

U(x) = a + bx, b > 0;

2) зростаюча функція корисності для суб'єкта керування несхильного до ризику

U(x) = log (x + b), x > - b;

3) зростаюча функція корисності з несхильністю до ризику

U(x) = a – be^-cx, b > 0, x ≥ 0;

4) зростаюча функція корисності зі схильністю до ризику

U(x) = x², x ≥ 0.

За своєю фізичною сутністю премія за ризик (надбавка за ризик) — це сума (в одиницях виміру критерію х, якою суб’єкт керування (особа, що приймає рішення) згоден знехтувати (поступитися нею) з середнього виграшу (тобто ця сума менша, ніж математичне сподівання виграшу) за те, щоб уникнути ризику пов'язаного з лотереєю.

Якщо особа, що приймає рішення зіштовхується з несприятливою для неї лотереєю (тобто лотереєю, що менш пріоритетна ніж стан, в якому вона у даний момент знаходиться), то природно виникає питання, скільки вона заплатила б (в одиницях виміру критерію х) за те, щоб не брати участі у цій лотереї (уникнути її).

На рис. 5.1 показано, як графічно можна зобразити ставлення особи до ризику. Крива ON, що задає рівень корисності (на осі ординат), котрий може бути досягнутий за відповідним рівнем доходу (відкладеного в тис. грн. на осі абсцис). Ця крива ілюструє несхильність особи до ризику.

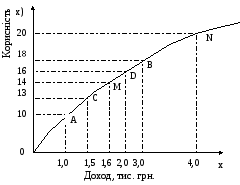
Рис. 5.1. Функція корисності особи, що несхильна до ризику

Міра несхильності до ризику. Локальна несхильність до ризику у деякій точці х визначається за допомогою функції несхильності:

r(x) = -U"(x)/U'(x).

Використовують також формулу:

r(x) = -(d/dx) [log U'(x)].