
- •2. Динамічні моделі оптимізації інвестиційних та інноваційних ресурсів
- •1) Рівняння балансу грошового потоку фірми
- •3. Основні принципи і задачі дослідження операцій. Розкрити їх зміст
- •4. Сутність та особливості економічної інформації
- •1.Класифікація екм. Двоїсті злп
- •2. Кількісні оцінки економічного ризику
- •3. Поняття імітаційної моделі та основні цілі імітаційного моделювання
- •4. Мета, задачі та принципи створення інформаційних систем
- •1. Етапи побудови та дослідження економічних моделей
- •2. Загальна постановка дискретної задачі оптимізації
- •3. Структура та властивості економічної інформації
- •4. Трендові моделі та їх характеристика. Сфери застосування в економічних процесах
- •5. Алгоритм методу потенціалів
- •6. Розвяок
- •1. Характеристика економіки окремих галузей як об'єкту математичного моделювання
- •2. Поняття та види моделей економічної динаміки
- •3. Методи знаходження опорного плану транспортної задачі (метод північно-західного кута, метод мінімального елементу, метод апроксимації Фогеля)
- •4. Призначення і роль інформаційної системи в економіці
- •1. Описати модель та задачу оптимізації споживання
- •2. Ціль та алгоритм дисперсійного однофакторного імітаційного експерименту
- •3. Структура і функції інформаційної системи управління
- •4. Функція колективної корисності. Егалітарна та утилітарна функції колективної корисності
- •Види та властивості функцій корисності
- •2. Методи кількісної оцінки ризиків
- •3. Структура інформаційного процесу управління
- •4. Розв'язок ігор в змішаних стратегіях
- •1. Задачі оптимізації споживання. Методи розв'язку та післяоптимізаційного аналізу
- •2. Ціль та алгоритм двохфакторного дисперсійного аналізу результатів імітаційних експериментів
- •3. Задачі управління, що реалізують інформаційний процес
- •4. Системний підхід у розробці, прийнятті та реалізації управлінських рішень
- •5. Рішення симплекс-методом, використовуючи перетворення Йордана-Гаусса.
- •6. Розрізняють два типи транспортних задач:
- •1. Поняття та властивості функції попиту на товари. Еластичність попиту
- •2. Поняття математичної гри та її застосування в дослідженні економічних систем
- •3.Етапи розвитку та створення інформаційних систем
- •4. Поняття та основні види виробничих функцій в економічних моделях
- •1. Основні моделі виробництва та їх властивості
- •2. Дати визначення опуклої функції та охарактеризувати її роль в задачах оптимізації.
- •3. Загальні особливості автоматизованих інформаційних систем
- •5. Розвязок
- •Поняття невизначеності та її врахування в ігрових задачах прийняття рішень
- •2. Поняття та види виробничої функції
- •3.Структура автоматизованих інформаційних систем
- •Методи імітації випадкових величин
- •1. Моделі ринкової рівноваги та їх характеристика
- •2. Що означає коефіцієнт дисконтування?
- •3. Архітектура автоматизованих інформаційних систем
- •4.Прийняття рішень в умовах невизначеності
- •Основні особливості моделювання економічних систем
- •2. Дати визначення стану економічної системи
- •3. Інформаційна технологія та її місце в інформаційній системі підприємства
- •Основні види бізнес-процесів підприємства
- •2. Характеристика моделей економічної динаміки
- •3. Сутність технологічного забезпечення та його місце в автоматизованій інформаційній системи
- •4. Охарактеризувати простір товарів і послуг в моделях споживання
- •6. Рішення симплекс-методом, використовуючи перетворення Йордана-Гаусса.
- •1. Моделювання олігополії як конкуренції небагатьох агентів
- •2. Класифікація математичних моделей економічних систем
- •3. Життєвий цикл інформаційної системи. Моделі життєвого циклу
- •4. Основні критерії прийняття рішень в умовах невизначеності
- •Розв язок
- •2. Етапи побудови економіко-математичних моделей
- •3. Основні види бізнес-процесів підприємства
- •4.Основні етапи впровадження інформаційної системи
- •6. Рішення симплекс-методом, використовуючи перетворення Йордана-Гаусса.
- •1. Поняття та сфери застосування імітаційних моделей
- •2. Основні види функцій колективної корисності
- •3. Стандарти управління підприємством crp та mrp
- •4. Що таке невизначеність в прийнятті рішень?
- •1. Поняття опуклої функції та її застосування в задачах оптимізації
- •2. Поняття математичної гри та її застосування в дослідженні економічних явищ
- •3. Стандарти управління підприємством mrp II та erp
- •4. Постановка задачі лінійного програмування
- •5. Рішення симплекс-методом, використовуючи перетворення Йордана-Гаусса.
- •Класифікація моделей економічної системи
- •2. Постановка задачі опуклого програмування та її застосування в економіці
- •3. Моделювання інформаційної системи підприємства за допомогою dfd діаграм
- •4. Основні види функції корисності в моделях споживання
- •5. Задача про вироби
- •1. Задачі формування і розподілу прибутків і затрат в моделях оптимізації економіки
- •2. Збалансовані та незбалансовані моделі транспортної задачі
- •3. Моделювання інформаційних систем підприємств за допомогою idef діаграм
- •4. Основні методи кількісної оцінки економічного ризику
- •6. Рішення симплекс-методом, використовуючи перетворення Йордана-Гаусса.
- •1. Стандарти сімейства idef
- •2. Базова модель лінійного програмування та її структура
- •Модель економічної рівноваги з гарантованим доходом
- •4. Поняття бізнес-процесу та процесного управління підприємством
- •1. Поняття та класифікація економіко-математичних моделей
- •2. Опорні плани задачі лінійного програмування
- •3. Case засоби моделювання інформаційних систем
- •Основні принципи і задачі дослідження операцій. Розкрити їх зміст
- •1. Двоїсті задачі лінійного програмування
- •2. Основні етапи впровадження інформаційних систем
- •3. Основні методи кількісної оцінки економічного ризику
- •4. Класифікація економіко-математичних моделей
- •6. Розвязок
- •1. Характеристика автоматизованої інформаційної системи обробки бухгалтерської інформації
- •2. Етапи побудови та дослідження економіко-математичних моделей
- •3. Поняття та алгоритм двохфакторного дисперсійного аналізу результатів імітаційних експериментів
- •4. Основні задачі дослідження операцій
- •1. Характеристика економіки як об’єкту моделювання
- •2. Комплекси задач (підсистеми) автоматизованих інформаційних систем бухгалтерського обліку
- •4.Методи знаходження опорного плану транспортної задачі (метод північно-західного кута, метод мінімального елементу, метод апроксимації Фогеля)
- •1. Види функцій корисності в моделях споживання
- •Модель автоматизованої інформаційної системи бухгалтерського обліку підприємства
- •4.Стандарти сімейства idef
- •5.Розвязок
- •1. Види та властивості функцій корисності
- •2. Основні методи імітації випадкових подій
- •3. Характеристика автоматизованої інформаційної системи менеджменту страхової діяльності
- •4. Розв'язок ігор в змішаних стратегіях
- •5. Симплекс-метод розв’язання задачі дробово-лінійного програмування
- •1. Задачі оптимізації споживання. Методи розв'язку та післяоптимізаційного аналізу
- •2. Основні методи лінійного програмування
- •3. Комплекси задач (підсистем) автоматизованої інформаційної системи страхової діяльності
- •4. Види економічної інформації
- •6. Розрізняють два типи транспортних задач:
- •1. Поняття та властивості функції попиту на товари. Еластичність попиту
- •2. Поняття та етапи побудови і дослідження імітаційних моделей
- •3. Модель автоматизованої інформаційної системи менеджменту страхової діяльності
- •4. Життєвий цикл інформаційної системи. Моделі життєвого циклу
- •1. Структура моделі виробництва та задачі оптимізації виробництва
- •3. Характеристика автоматизованих інформаційних систем менеджменту банківської діяльності
- •4. Основні критерії прийняття рішень в умовах ризику
- •1. Поняття та види виробничої функції
- •2. Структура та властивості економічної інформації
- •3.Комплекси задач (підсистеми) автоматизованих інформаційних систем банківської діяльності
- •4.Поняття та етапи побудови і дослідження імітаційних моделей
- •1. Моделі ринкової рівноваги та їх характеристика
- •2. Що означає коефіцієнт дисконтування?
- •3. Модель автоматизованої інформаційної системи банківської діяльності
- •4. Основні види бізнес-процесів підприємства
- •5. Задача про будівництво
- •1. Поняття та характеристики економічної системи
- •2. Характеристика автоматизованої інформаційної системи Держаної статистичної служби України
- •3. Сутність інформаційного процесу управління
- •4. Види функцій корисності в моделях споживання
- •1. Модель міжгалузевого балансу та її характеристика
- •2. Види економічної інформації
- •3. Комплекси задач (підсистеми) автоматизованої інформаційної системи Державної статистичної служби України
- •4. Поняття математичної гри та її застосування в дослідженні економічних систем
- •6. Рішення симплекс-методом, використовуючи перетворення Йордана-Гаусса.
- •1. Задачі оптимізації виробництва підприємства-монополіста
- •2 . Класифікація економіко-математичних моделей
- •3. Основні етапи впровадження інформаційних систем
- •4. Основні критерії прийняття рішень в умовах невизначеності
- •1. Основні етапи побудови і дослідження економіко-математичних моделей
- •2. Case засоби моделювання інформаційних систем підприємств
- •3. Види виробничих функцій
- •4. Основні задачі дослідження операцій
- •6. Рішення симплекс-методом, використовуючи перетворення Йордана-Гаусса.
- •1. Особливості моделювання виробничого процесу підприємства-монополіста
- •2. Основні види функцій колективної корисності
- •3. Основні види бізнес-процесів підприємства
- •4. Модель автоматизованої інформаційної системи страхової діяльності
- •1. Структура та властивості економічної інформації
- •2. Етапи побудови і дослідження імітаційних моделей
- •3. Комплекси задач (підсистеми) автоматизованої інформаційної системи банківського обліку
- •Поняття економічного ризику
- •5. Рішення симплекс-методом, використовуючи перетворення Йордана-Гаусса.
- •1. Стандарти управління підприємством crp та mrp
- •2. Описати модель економічної рівноваги
- •3. Види задач дослідження операцій
- •4. Види функцій корисності в моделях споживання
- •1. Збалансовані та незбалансовані моделі транспортної задачі
- •2. Класифікація економіко-математичнх моделей
- •3. Стандарти сімейства idef
- •4.Поняття економічного ризику
- •6. Рішення симплекс-методом, використовуючи перетворення Йордана-Гаусса.
- •Базова модель лінійного програмування та її структура
- •Реінжінірінг бізнес-процесів
- •Стандарти управління підприємством mrp II та erp
- •Основні критерії прийняття рішень в умовах ризику
1. Структура моделі виробництва та задачі оптимізації виробництва
Технологія побудови моделі використовує такі потужні наукові методи, як метод системного
аналізу, структурного синтезу, оптимізації, теорії графів.
Середовище функціонування підприємства розглядається як система, а підприємство – як
підсистема, що функціонує у цьому середовищі і зв’язане з ним через певні параметри.
В основу проектного процессу закладені положення щодо взаємодії
середовища і процесу проектування. Середовище приймає запит на створення об’єкта проекту-
вання, узгоджує умови обміну даними між проектними процесами, керує цими процесами, забез-
печує ефективний розподіл ресурсів, управляє накопиченими і представленими даними.
Для побудови нової моделі складного виробничого комплексу необхідні:
– запит середовища, тобто потреба в продукції підприємства;
– ресурси для реалізації такої структури (матеріали, енергія, працівники, інформація, ін.);
– знання про об’єкт, що створюється, і управління створеною структурою з метою досягнення
визначеного наперед показника ефективності.
Структура виробничого комплексу містить набір функціонуючих підструктур, які загалом забезпечать на виході продукт із заданими характеристиками. Такі характеристики апріорі визначені як
конкурентоспроможні. Як базову підструктуру приймають безпосередньо виробниче підприємство,
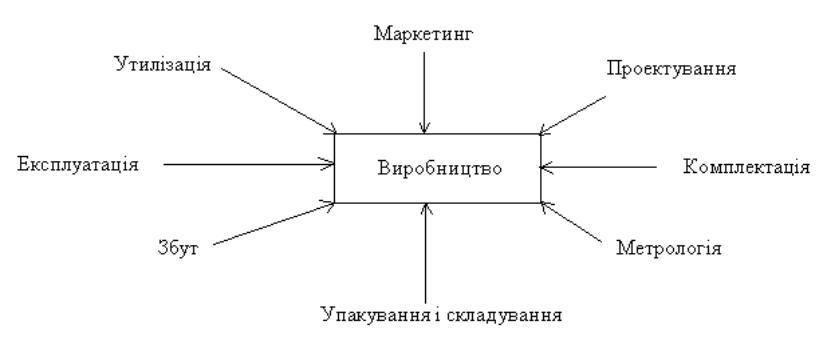
а інші функції долучають до його складу. Схематично таку структуру можна відобразити у такому вигляді:
Рис. 1. Схема структури моделі
Розрізняють: задачі безумовної оптимізації, задачі умовної оптимізації, задачі математичного програмування, задачі опуклого програмування, чисельні методи оптимізації. Зада́ча оптиміза́ції — задача знаходження точки (точок) мінімуму, або декількох мінімумів заданої функції.Формальне визначення Нехай задано деяку множину X із n-вимірного евклідового простору і функцію f(x), визначену на X. Необхідно знайти точки мінімуму значень функції f(x) на X. Або: f(x) → min, x ∈ X. тут f(x) — цільова функція, X — допустима множина, кожна точка x цієї множини — допустима точка задачі. Також, задачу оптимізації можна сформулювати як пошук максимуму (максимумів) цільової функції: f(x) → max, x ∈ X. ця задача еквівалентна попередній задачі мінімізації цільової функції із знаком мінус, в тому сенсі, що множини їхніх розв'язків збігаютьсяРозв'язки задачі
Розв'язки задачі можна розділити на дві множини: глобальні (глобального мінімуму), це такі допустимі точки x* в яких цільова функція має найменше значення на всій допустимій області: f(x*) ≤ f(x), ∀ x ∈ X; Локальні (локального мінімуму), це такі допустимі точки x* в яких цільова функція приймає найменше значення в деякому околі: f(x*) ≤ f(x), ∀ x ∈ X ∩ Uε(x*), Де Uε(x*) = {x ∈ Rn | ‖x — x*‖ ≤ ε} — куля радіусу ε в центрі x*2. Дати визначення опуклої функції
Загальна задача математичного програмування формулюється так: знайти такі значення змінних xj , щоб цільова функція набувала екстремального (максимального чи мінімального) значення:
(8.1)
за умов:
( ); (8.2)
. (8.3)
Якщо всі функції та , є лінійними, то це задача лінійного програмування, інакше (якщо хоча б одна з функцій є нелінійною) маємо задачу нелінійного програмування.
Розглянемо задачу нелінійного програмування, яку, не зменшуючи загальності, подамо у вигляді:
, (8.22)
, (8.23)
. (8.24)
Нехай задано n-вимірний лінійний простір Rn. Функція , що задана на опуклій множині , називається опуклою, якщо для будь-яких двох точок та з множини X і будь-яких значень виконується співвідношення:
. (8.27)
Якщо нерівність строга і виконується для , то функція називається строго опуклою.
Якщо нерівність строга і виконується для , то функція називається строго опуклою.
Нехай — точка, в якій . Тоді в точці досягається локальний мінімум, що збігається з глобальним.
