2.1.2.1 Равномерное распределение

Самым простым, но редко встречающимся в практике обеспечения качества, является равномерное распределение (или равномерное непрерывное распределение). Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.

Пример. Шкала измерительного прибора проградуирована в некоторых единицах. Ошибку при округлении отсчета до ближайшего целого можно рассматривать как случайную величину , которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями. Таким образом,имеет равномерное распределение.

Пусть будет наименьшим, анаибольшим возможным значением непрерывного признака качества. На интервалеполучим равномерное распределение переменной , если вероятность появления значения на любом участке интервалапропорциональна длинеэтого участка:

для всех . (2.39)

Функция равномерного распределения имеет вид:

для ,

для ,

для .

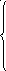
(2.40)

Для равномерного распределения плотность составляет:

при ,

в противном случае.

(2.41)

На рис.2.8 показаны графики плотности и функции распределения равномерного распределения при и.

По графикам становится понятно, почему это распределение называется равномерным. Если график плотности распределения непрерывной случайной переменной имеет вид треугольника, лежащего на оси абсцисс, то говорят о треугольном распределении.

Функция, обратная к (2.40), то есть квантильная функция равномерного распределения, имеет вид:

; .

Равномерное распределение имеет следующие числовые характеристики:

- математическое ожидание:

; (2.42а)

- дисперсия:

; (2.43б)

- асимметрия:

. (2.42в)

Рис.2.8. Равномерное распределение на интервале

Равномерное распределение не воспроизводимо. Так, например, сумма двух равномерно распределенных случайных переменных распределена по закону треугольника.

Важным частным случаем равномерного распределения является распределение на интервале . Оно используется для генерирования случайных чисел, имеющих заданное распределение. Для этого в квантильную функцию случайной переменной, реализацию которой нужно определить, вводят в качестве аргумента число, равномерно распределенное на интервале.

Кроме того, равномерное распределение реализуется в опытах, где наудачу ставится точка на отрезке , а также в экспериментах по измерению тех или иных физических величин с округлением (- ошибка округления).

Обобщением распределения, равномерного на интервале , является бета-распределение. Непрерывная случайная переменнаяимеет бета-распределение, если ее плотностьимеет вид:

при ,

в противном случае.

(2.43а)

с параметрами распределения и. Функция распределениябета-распределения имеет вид:

для ,

для ,

для .

(2.43б)

Бета-распределение с параметрами исовпадает с равномерным распределением на интервале.

Числовые характеристики бета-распределения:

- математическое ожидание

, (2.44а)

- дисперсия

. (2.44б)

Пример 2.16. Случайная величина задана плотностью распределения

0 при ;

при ;

0 при .

Найти коэффициент .

Плотность распределения должна удовлетворять условию . Настоящее равенство выполняется в том случае, когда. Тогда.

Пример 2.17. Случайная величина задана плотностью распределения

при ;

при .

при ;

Найти функцию распределения и вероятность того, что в результате испытания случайная величина примет значение, заключенное в интервале .

Если , то , следовательно, . Если , то, следовательно, . Если , то . Вероятность того, что в результате испытания случайная величина примет значение, заключенное в интервале , равна .

Пример 2.18. Приведите вывод формулы(2.42а)

.