2.2 Статистическая проверка статистических гипотез

Как уже упоминалось ранее, статистическое обеспечение качества – это прикладная теория проверки статистических гипотез, хотя в области обеспечения качества подлежащая проверке гипотеза не всегда четко формулируется.

Статистическая гипотеза - это любое предположение, касающееся распределения случайной величины или неизвестного значения параметра этого распределения или, другими словами, предположения о свойствах случайной величины.

Статистическими могут являться, например, гипотезы:

- генеральная совокупность распределена по закону Пуассона;

- дисперсии двух нормальных совокупностей равны между собой.

В первой гипотезе сделано предположение о виде неизвестного распределения, а во второй о параметрах двух известных распределений.

Примечание. Гипотеза «на Марсе есть жизнь» не является статистической, поскольку в ней не идет речь ни о виде, ни о параметрах распределения.

Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая ей гипотеза.

Нулевой (основной) называют гипотезу, подлежащую проверке (гипотеза ).

Конкурирующей (альтернативной) называют гипотезу, которая противоречит нулевой (гипотезу ).

Например, если нулевая гипотеза состоит в предпо­ложении, что математическое ожидание нормального распределения равно, то конкурирующая гипотеза, в частности, может состоять в предположении, чтоили. Коротко это записывают так:

;

или .

Различают простые и сложные гипотезы.

Простой называют гипотезу, содержащую только одно предположение и которая полностью задает распределение совокупности Например, если - параметр показатель­ного распределения, то гипотеза- простая. Ги­потеза: математическое ожидание нормального рас­пределения равно(известно) - простая.

Сложной называют гипотезу, которая состоит из ко­нечного или бесконечного числа простых гипотез и не полностью задает распределение совокупно­сти. Напри­мер, сложная гипотеза состоит из бесчисленного множества простых вида, где- любое число, большее 5. Гипотезаматематическое ожидание нормального распределения равно(неизвестно) - сложная.

Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят статистическими методами, ее называют статистической.

В области обеспечения качества предположения связываются с нормами на признаки качества продукции. Метод проверки статистической гипотезы путем анализа выборки из генеральной совокупности называется статистическим критерием (тестом) для проверки гипотезы или просто критерием.

В зависимости от содержания проверяемых гипотез различают параметрические и непараметрические критерии (критерии согласия). С помощью параметрических критериев проверяется гипотеза относительно значенияпараметраданного распределения типа(простая или точечная гипотеза) или некоторой области его значений, например, или(сложная гипотеза). В обеспечении качества, как правило, имеют дело со сложными гипотезами. С помощью непараметрических критериев (критериев согласия), проверяют гипотезу о предполагаемом законе неизвестного распределения.

В силу того, что статистический критерий основывается на свойствах выборки, а тем самым на зависящем от случая результате, то нельзя дать обоснованного доказательства или опровержения гипотезы. Утверждения статистического критерия не имеют такой силы. Принятие гипотезы не означает, что она истинна, а ее отклонение не означает, что она ложна. В любом случае при использовании статистического критерия возможно ошибочное решение.

Существуют два варианта принятия ошибочного решения при использовании статистического критерия (табл.2.4).

Таблица 2.4. Виды ошибок при проверке статистических гипотез

Результат проверки гипотезы	Действительное положение дел
	истинна	ложна
принимается	верное решение	ошибка 2-го рода (-ошибка)
отклоняется	ошибка 1-го рода (-ошибка)	Верное решение

Гипотеза может быть верна, но ее отвергают согласно критерию. Это ошибочное решение (отклонение правильной гипотезы) называется ошибкой первого рода. Вероятность ее появления обозначается , поэтому ее называют ошибкой. Вероятность являетсяуровнем значимости критерия. При приемочном контроле ошибка первого рода приводит к браковке партии с допустимой долей брака (так называемый риск производителя), а при контроле производства - к вмешательству в налаженный процесс производства (ложная тревога).

Другое возможное заблуждение – принятие гипотезы , которая в действительности неверна. Эта ошибка называетсяошибкой второго рода или ошибкой, причем является вероятностью появления ошибки второго рода. При приемочном контроле ошибка второго рода приводит к принятию партии с недопустимой долей брака (так называемыйриск потребителя), а при контроле производства - к невмешательству в производственный процесс, вышедший за допустимые границы (пропуск перехода).

Примечание. 1. Правильное решение может быть принято также в двух случаях:

- гипотеза принимается, причем и в действительности она пра­вильная;

- гипотеза отвергается, причем и в действительности она неверна.

2. Наи­более часто уровень значимости принимают равным 0.01, 0.05 или 0.1. Если, например, принят уровень значимости, равный 0.05, то эго означает, что в пяти случаях из ста имеется риск допустить ошибку первого рода (отвергнуть правильную гипотезу).

Значения риска потребителя при контроле производителя определяются табл.2.5 и табл.2.6.

Таблица 2.5. Нормативные значения риска потребителя

Степень доверия	Нормативные значения риска потребителя
1	2
Т1 – требование сплошного контроля продукции перед поставкой потребителю	0.00
Т2 – отсутствие надежной информации о возможностях поставщика обеспечить требуемое качество или информация о низком качестве его поставок, отрицательные отзывы других потребителей	0.10
Т3 – отсутствие сертификата на продукцию и систему обеспечения качества, отсутствие собственного опыта заказов у данного поставщика, отсутствие процедур статистического управления технологическими процессами, но при учете косвенной положительной информации от других потребителей или обществ потребителей	0.25
Т4 – отсутствие у поставщика сертификата на систему обеспечения качества, но при наличии сертификата на продукцию и продолжительного периода поставок продукции удовлетворительного качества, положительная оценка системы качества самим потребителем, внедрение статистического управления технологическими процессами на отдельных этапах производства	0.50
Т5 – наличие сертификата на систему обеспечения качества по ГОСТ Р ИСО 9003, применение поставщиком процедур статистического управления технологическими процессами, долговременные поставки высококачественной продукции и т.д.	0.75

Продолжение таблицы 2.5

Т6 – Наличие у поставщика сертификата на систему обеспечения качества по ГОСТ Р ИСО 9001 или ГОСТ Р ИСО 9002, применение поставщиком процедур статистического управления технологическими процессами, положительный опыт собственных заказов у данного поставщика и т.п.	0.90
Т7 – наличие у поставщика сертификата на систему обеспечения качества по ГОСТ Р ИСО 9001, сертификата на производство, безупречная репутация поставщика, применение поставщиком процедур статистического регулирования технологическими процессами, длительный период поставки продукции без претензий и т.п.	1.00

Характеристики, определяющие ту или иную степень доверия в табл.2.5, устанавливает потребитель в собственной нормативной документации. Расширенная табл.2.6 позволяет более точно оценить доверие к поставщику.

С другой стороны, защита потребителя через уменьшение нормативного значения условного риска является дорогостоящим средством. На рис.2.12 представле­на зависимость объемов контроляот риска потребителя . Видно, как быстро растет объем контроля, а следовательно, затраты на контроль с уменьшением .

В тех случаях, когда априорная вероятность получения партий продукции несо­ответствующего качества мала, например меньше …, нет необходимости устанавливать малое значение . Это приводит только к удорожанию контроля.

Таблица 2.6. Расширенная таблица степеней доверия

Степень доверия	Нормативное значение риска потребителя при контроле поставщика
1	2
Т1	0.00
Т2	0.10
Т3	0.25
Т4	0.50
Т5	0.60
Т6	0.70
Т7	0.80
Т8	0.90
Т9	0.95
Т10	1.00

Следует отметить, что потребитель имеет право самостоятельно устанавливать (без согласования с кем-либо). Если потребитель не имеет уверенности в достоверности информации о качест­ве поставляемой продукции, то обычно применяют .

В теории приемочного контроля очень важным моментом является задание вероятностей ошибок. В силу того, что иозначают риск производителя (поставщика) и риск потребителя, то их определение отвечает интересам обеих сторон. Представляет интерес, каким образом связаны между собой вероятности ошибок первого и второго рода, и влиянию каких параметров они подвержены.

Рис.2.12. Зависимость объема выборок для одноступенчатого (верхняя кривая) и двухступенчатого(нижняя кривая) контроля от риска потребителя при контроле поставщика для объема партии

Предположим, имеется некий химический реактор, который может работать только в одном из двух состояний. Если он работает в налаженном режиме, то для интересующего нас признака качества, например концентрации вещества, имеет место . В разлаженном режиме. Оба режима отличаются только уровнем настройки процесса, в то время как дисперсия в обоих случаях составляет.

Проверить нужно нулевую гипотезу, в соответствии с которой , против единственно возможной альтернативы. Тогда:

^;

.

Итак, необходимо определить, в каком из состояний работает аппарат. В рассматриваемом случае не имеет большого значения, какую из гипотез выбирают в качестве нулевой гипотезы .

Чтобы провести проверку, возьмем выборку из потенциально бесконечной генеральной совокупности объемом (выборка без возвращения). В качестве контрольной величины возьмем выборочное среднее, которое является несмещенной и эффективной оценкой параметра. Если верна гипотеза, то. При верностиимеем.

Примечание. Дисперсия среднего арифметического одинаково распределенных взаимно независимых случайных величин враз меньше дисперсиикаждой из величин:

.

На рис.2.13 изображены плотности распределения при верности гипотезы(плотность распределения 1) или гипотезы(плотность распределения 2).

Как видно из рис.2.13, реализация возможна при верности любой из двух гипотез, но с различной вероятностью.

Для формулировки критерия разделим область изменения контрольной величины на критическую область (critical region) – область отклонения гипотезы и дополнительную к ней область – область принятия гипотезы .

Из рис.2.13 следует, что выполнение условия возможно при верности гипотезы. В этом случаеошибочно отвергается, то есть происходитошибка первого рода. Но возможно также выполнение , если верна гипотеза. В этом случае ошибочно принимается, то есть происходитошибка второго рода.

Область принятия

гипотезы

Область отклонения

гипотезы

Рис.2.13. Распределение контрольной величины и критическая область

Вероятность совершения ошибки первого рода формально задается выражением или(отклоняетсяпри верности).

Вероятность ошибки второго рода или(принимаетсяпри верности).

В данном случае с ив силуполучаем при расчете вероятностей ошибок:

, (2.67)

. (2.68)

Приведенные соотношения и анализ рис.2.13 показывают, что:

• увеличение объема выборки ведет к уменьшению дисперсии [] выборочной среднейи тем самым к одновременному уменьшению вероятности ошибок обоих видов;

• сумма ине равна ни единице, ни какой-то другой постоянной величине. Вероятность ошибок обоих решений – принятия или отклонения гипотезы, относится к различным плотностям распределения (кривые 1 и 2 на рис.2.13);

• увеличение ведет к уменьшению, но к одновременному увеличению, а уменьшениеприводит к увеличениюи уменьшению.Отметим, что одновременное уменьшение значений ивозможно только за счет увеличения объема выборки. Кроме того, и есть условные вероятности с соответственно разными условиями. Это объясняет то, что сумма и не равна единице. Единицей является площадь под кривой плотности распределения на рис.2.13;

• задавая значения , то есть уровень значимости критерия, тем самым определяем область отклонения гипотезы. Наиболее распространенными значениямиявляются 0.1; 0.05; 0.01; 0.001;

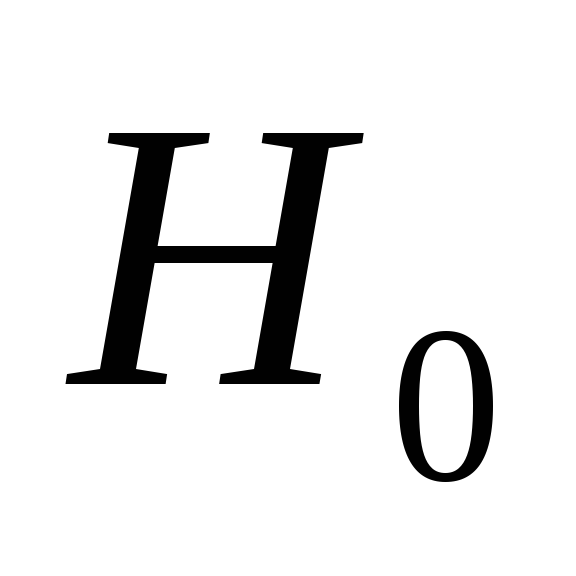• вероятность ошибки первого рода относится к критерию проверки гипотез в целом, а не к отдельному результату проверки. Отсюда следует, что если проверка проводится многократно, то примерно вслучаях гипотезаможет быть отклонена даже, если она в действительности верна.

Зависимости (2.67) и (2.68) содержат четыре величины: ,,и. Задав численно две их них, можно найти две другие. Например, пусть,,,и. Этим задается критерий проверки гипотезы. Определим вероятности ошибок:

;

.

Если заданы и, то можно определить соответственнои, то есть найти сам критерий.

При определении области отклонения гипотезы необходимо, во-первых, учитывать, что максимальная вероятность ошибки первого рода должна быть не больше, чем заданный уровень значимости критерия , а во-вторых, вероятность ошибки второго рода должна быть как можно ниже. Вероятность ошибок обоих видов можно определить, используя зависимости (2.67) и (2.68), то есть оперативную характеристику критерия.

Соотношение между и, сумма которых, как было отмечено выше, не равна ни единице, ни какой-то другой постоянной величине, для случая проверки простой гипотезыпротивпоказана на рис.2.13.

Кривая 1 (рис.2.13) при получается из (2.67) и (2.68) следующим образом: припо (2.67) определяем сначалаи затем определяем. Этииподставляем в (2.68) и получаем соответствующеезначение .

Таким образом, каждой паре значений исоответствует свое значение. Проверка гипотез при большом объеме выборкиприводит к уменьшению вероятностей обеих ошибок (рис.2.14). Задавая значения, т.е. уровень значимости критерия, тем самым определяют область отклонения гипотезы.

Рис.2.14. Соотношение вероятностей ошибок при различных объемах выборок

При определении области отклонения гипотезы необходимо, во-первых, учитывать, что максимальная вероятность ошибки первого рода должна быть не больше, чем заданный уровень значимости критерия , а во-вторых, вероятность ошибки второго родадолжна быть как можно меньше.

Пример 2.29. Решите для всех имеющихся шести возможностей при заданных двух величинах из четырех систему уравнений (2.67) и (2.68). Выбирайте при этом значения ;;;;. Округлите значениядо следующего целого числа.

Случай 1. Задано и.

При известных ис помощью таблицы нормированного нормального распределениянаходим:

,

.

Случай 2. Задано и .

При известных ис помощью таблицы квантилей нормированного нормального распределениянаходим:. Тогда. Получаем, что.

Тогда .

Случай 3. Задано и.

При известных и, находим:

Тогда

Случай 4. Задано и.

При известных и, получим:

Округляем до ближайшего целого числа в сторону увеличения, получаем

Для расчета получаем:

Случай 5. Задано и.

При известных и, получим:

Для расчета получим:

Случай 6. Задано и.

При известных и, получим:

Пример 2.30. Составьте для случая проверки гипотезы случай с против с критической областью уравнения дляи, аналогичные (2.67) и (2.68). Постройте для этого график, подобный рис.2.14.

В силу получаем при расчете вероятностей ошибок следующие зависимости (см. рис.2.15):

, (2.69)

. (2.70)

Рис.2.15. Соотношение вероятностей ошибок при различных объемах выборок