3.3.1.5 Сравнение трех оперативных характеристик

Р оперативную характеристику ассмотрим более подробно и сравним друг с другом гипергеометрическую оперативную характеристику , биномиальную оперативную характеристикуи ха­рактеристику Пуассона.

Сначала отметим, что три названные оперативные характеристики строго монотонно убывают и совпадают при :

. (3.71а)

Строгая монотонность убывания оперативной характеристики означает, что среди партий с различными долями брака партия с наименьшей засоренностью имеет наибольшую вероятность приемки. При значения гипергеометрической и биномиальной оперативных характеристик равны нулю, в то время как оперативная характеристика Пуассона принимает некоторое положительное значение (см. также пример 3.26):

. (3.71б)

Все три функции определены на интервале только для дискретных значенийпри. Однако область определения оперативных характеристик

, (3.72)

(3.73)

легко расширяется на все , непрерывно заполняющие интервал, так как слагаемые в (3.72) и (3.73) вычисляются при каждом. Функции (3.72) и (3.73) в интерваленепрерывны и даже дифференцируемы:

, (3.74)

. (3.75)

Гипергеометрическую оперативную характеристику

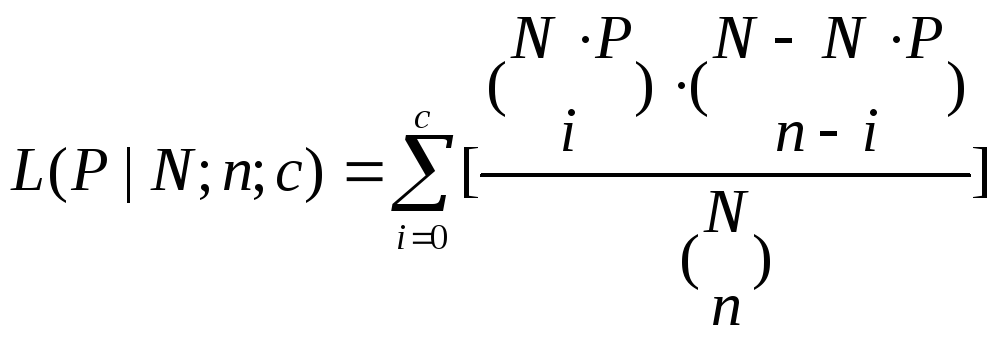(3.76)

с учетом выражения биномиальных коэффициентов в (3.76) через гамма-функции (это выражение следует из определения биномиальных коэффициентов )

(3.77)

также можно определить на всем интервале . Однако получаемые после дифференцирования выражения длякрутизны оперативной характеристики оказываются слишком сложными. Для упрощения задают крутизну оперативной характеристики: каждую точку графикагипергеометрической оперативной характеристики связывают прямой со стоящей справа точкойи определяют подъем этой прямой как крутизну функциив точке. Наклон прямойвычисляется по формуле

, (3.78)

причем

. (3.79а)

Вывод соотношения (182) иллюстрирует рис.3.23.

Рис.3.23 Крутизна гипергеометрической оперативной характеристики

Кроме того, для приращения (183а) справедливо выражение

при (3.79б)

Если при уровне дефектности первые производные (3.74) и (3.75) или крутизна (3.78) достигают максимума, то это значениеназываетсяточкой перегиба оперативной характеристики. Оперативные характеристики, не имеющие точек перегиба, внутри всей области определения будут везде выпуклыми или вогнутыми. Если оперативная характеристика имеет точку перегиба , то она выпуклая в области от нулевой точки до точки перегиба, а начиная с точки перегиба - вогнутая. Например, на рис.3.18 видно, что функцияглобально вогнутая, в то время как функцияна некоторых участках вогнутая, а на некоторых выпуклая.

На этом примере становится ясно, что точка перегиба появляется лишь при некоторых значениях приемочного числа (). Рассмотрим три воз­можных случая:и.

В случае все три оперативные характеристики вездевогнуты, то есть не имеют точек перегиба, и поэтому

для , (3.80)

то есть оперативные характеристики внутри открытого интервала не пересекаются.

В случае , который возможен только при очень малых объемахвыборки, только функцияимеет точку перегиба, то есть на некоторых участках она являетсявыпуклой, а на некоторых - вогнутой. Функции ивездевыпуклы и имеет место:

для . (3.81)

График функции пересекает графики функцийив интервалевсего один раз.

В случае все три функции имеют точки перегиба, то есть на опре­деленных участках они являютсявыпуклыми, а на других - вогнутыми. Точки перегиба определяются как

для , (3.82а)

для , (3.82б)

для . (3.82в)

Три оперативные характеристики пересекаются в интервале по одному разу.

Модуль крутизны в точке перегиба оперативной характеристики является мерой мощности критерия простого плана контроля или, что тоже самое, стоящей за ним процедуры проверки гипотезы (3.52). Крутизну в этой точке называюткрутизной оперативной характеристики. Крутизну получают путем подстановки формул (3.82а) - (3.82в) в (3.74), (3.75) и в (3.78):

для , (3.83а)

для , (3.83б)

для . (3.83в)

В выражении (3.83в) применяется обозначение . Значения кру­тизныпри безразличном качестве используют в качестве приближения для (3.83а – 3.83в).

Формулами (3.74), (3.75) и (3.78) определяется крутизна оперативных характеристик. Это позволяет вычислить их относительную крутизну. При этом только для оперативной характеристики Пуассона получается приелемая для расчетов формула

. (3.84)

Поскольку функция при безразличном качествепринимает значение, выражение (3.84) в точкедостигает значения

. (3.85а)

Зависимость (3.85а) имеет приближение

. (3.85б)

Если оперативная характеристика Пуассона имеет точку перегиба с абсциссой , то есть, то она близка к точкеи тогда с помощью формул (3.85) можно получить приблизительное значение относительной крутизныоперативной характеристики Пуассона в точке перегиба.

Пример 3.31 Пусть , то есть мы имеет дело с самым важным для практики случаем, когда. Для этого плана () сравним гипергеометрическую оперативную характеристику

и аппроксимирующие ее выражения биномиального распределения и распределения Пуассона

,

.

Результаты вычислений представлены в таблице

0	1	1	1
0.02	1	0.9996	0.9994
0.04	1	0.9969	0.9957
0.06	0.9971	0.9904	0.9871
0.08	0.9895	0.9789	0.9727
0.10	0.9758	0.9619	0.9526
0.12	0.9556	0.9392	0.9269
0.14	0.9287	0.9109	0.8964
0.16	0.8954	0.8774	0.8617
0.18	0.8563	0.8392	0.8238
0.20	0.8122	0.7969	0.7834
0.22	0.7640	0.7514	0.7413
0,24	0.7125	0.7033	0.6983
0.26	0.6590	0.6535	0.6550
0.28	0.6042	0.6027	0.6120
0.30	0.5492	0.5518	0.5697
0.32	0.4947	0.5013	0.5285
0.34	0.4417	0.4519	0.4887
0.36	0.3907	0.4042	0.4506
0.38	0.3423	0.3585	0.4143
0.40	0.2969	0.3154	0.3799

Кривые, по крайней мере, до точки почти не отличаются друг от друга, поэтому не будем изображать их графически. Кроме того, из таблицы видно, что кривые пересекаются по одному разу:ив грубом приближении при,, а такжеипри.

В силу того, что , все три оперативные характеристики имеют точки перегиба, абсциссы которых по (3.82) составляют

,

,

.

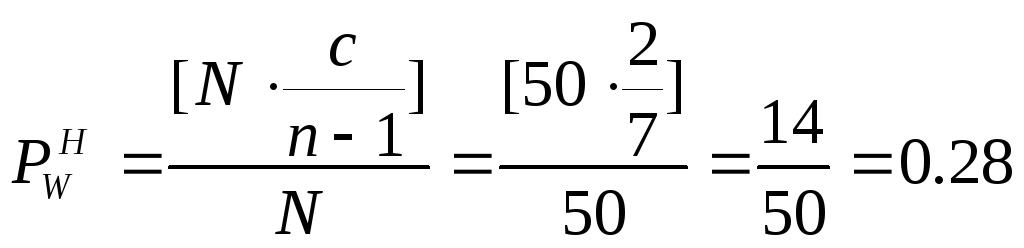Крутизна в точке перегиба составляет

,

,

.

Таким образом

,

то есть план контроля () и критерий проверки соответствующей гипотезы при работе с контролируемой величиной(число дефектных изделий в выборке), подчиняющейся гипергеометрическому распределению, имеют наи­большую мощность.

Крутизну можно выразить еще и через угол . Например, результатозначает, что в точке перегибакасательная к графикуобразует с отрицательным направлением осиугол, для которого, то есть. Поэтому угол наклона касательной в точкесоставляет приблизительно. Соответственно изследует, что функцияимеет касательную в точкес наклоном. Изследует, что отрезок, связывающий значение функцийв точкахи, имеет с горизонтальной осью угол.