
- •1. Основные положения статистической термодинамики
- •1.1. Понятия и начала феноменологической термодинамики.
- •1.2. Микроскопическое (механическое) описание классических систем.
- •1.3. Особенности представления квантовых систем
- •1.4. Вероятность нахождения системы в элементе фазового пространства. Метод ансамблей Гиббса.
- •1.5. Макроскопические величины как фазовые средние
- •1.6. Распределение в системах с постоянным числом частиц
- •1.6.2. Распределения Гиббса.
- •1.6.3. Квазиклассическое приближение.
- •1.7. Свойства распределения Гиббса
- •1.8. Большое каноническое распределение Гиббса
- •2. Статистика идеального газа
- •2.1. Идеальный газ как модель статистической системы
- •2.2. Распределение Максвелла
- •2.3. Столкновения молекул со стенкой сосуда. Давление
- •2.4. Характерные величины идеального газа
- •2.5. Столкновение молекул между собой
- •2.6. Длина свободного пробега
- •2.7. Идеальный газ во внешнем поле
- •2.8. Число и функция состояний идеального газа
- •2.9. Классическая теория теплоемкости газа двухатомных молекул
- •2.10. Квантовая теория теплоемкости газа двухатомных молекул
- •2.11. Распределения в квантовых системах
- •3. Законы термодинамики
- •3.1. Статистическое обоснование первого начала термодинамики
- •3.2. Второе начало термодинамики
- •3.3. Вечный двигатель второго рода. Максимальная работа процессов
- •3.4. Полезная работа тепловых машин
- •3.5. Метод термодинамических потенциалов
- •3.6. Термодинамические коэффициенты. Критерии устойчивости равновесия
- •3.7. Статистическое вычисление термодинамических величин
- •3.8. Третье начало термодинамики (теорема Нернста)
- •3.9. Применения термодинамики
- •4. Статистика сложных систем.
- •4.1. Модель кристаллического твердого тела. Уравнение движения атомов
- •4.2. Дисперсионное уравнение нормальных колебаний кристалла
- •4.3. Кристалл как система линейных гармонических осцилляторов
- •4.4. Статистическая сумма и энергия кристалла (в гармоническом приближении)
- •4.5. Теория теплоемкости Дебая
- •4.6. Электронный газ в металлах
- •4.7. Зависимость энергии электрона от волнового вектора. Эффективная масса
- •4.8. Теория парамагнетизма. Природа и характеристики магнетизма.
- •4.9. Равновесное излучение.
- •4.10. Системы с кулоновским взаимодействием частиц.
- •5. Теория малых флуктуаций
- •5.1. Определение и значение флуктуаций
- •5.2. Мера вероятности и масштаб флуктуаций
- •5.3. Флуктуации термодинамических величин в однородной среде
- •5.4. Предельная чувствительность измерительных приборов
- •5.5. Рассеяния света флуктуациями
- •6. Элементы теории физической кинетики
- •6.1. Определения и характеристики необратимых процессов
- •6.2. Теория стационарных процессов в газе свободных электронов
- •6.3. Газокинетическое уравнение Больцмана
- •6.4. Приближение времени релаксации
- •Раздел 2
- •Раздел 2
- •Раздел 3
- •Раздел 4
- •Раздел 5
- •Раздел 6
- •Список Литературы
2.6. Длина свободного пробега
Средний путь,
проходимый молекулой между двумя
последовательными соударениями,
называется средней длиной свободного
пробега. За одну секунду молекула
проходит в среднем расстояние, равное
средней тепловой скорости
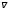 .
За это время она испытывает
.
За это время она испытывает
 столкновений (2.21); и средняя длина
свободного пробега оказывается обратно
пропорциональна плотности газа и
эффективному сечению
:
столкновений (2.21); и средняя длина
свободного пробега оказывается обратно
пропорциональна плотности газа и
эффективному сечению
:
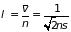 (2.22)
(2.22)
Практический
интерес представляет вероятность того,
что молекула пройдет произвольный путь
 ,
не испытав ни одного столкновения, или,
иными словами, закон распределения
вероятностей для пробега молекул.
Обозначим искомую вероятность через
,
не испытав ни одного столкновения, или,
иными словами, закон распределения
вероятностей для пробега молекул.
Обозначим искомую вероятность через
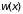 .
Тогда
.
Тогда
 – вероятность безстолкновительного
прохождения пути
– вероятность безстолкновительного
прохождения пути
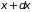 .
Это событие сложное, состоящее из двух
независимых, поэтому, согласно теореме
умножения вероятностей,
.
Это событие сложное, состоящее из двух
независимых, поэтому, согласно теореме
умножения вероятностей,
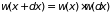 .
.
Очевидно, что
вероятность
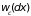 ,
что на бесконечно малом отрезке пути
,
что на бесконечно малом отрезке пути
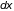 молекула испытает соударение,
пропорциональна его длине, т.е.
молекула испытает соударение,
пропорциональна его длине, т.е.
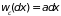 или
или
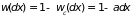 .
После представления
рядом по степеням
[
.
После представления
рядом по степеням
[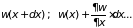 ]
исходное уравнение и его решение примут
вид
]
исходное уравнение и его решение примут
вид
 ;
;
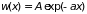 .
.
Событие – пролёт
молекулой сколь угодно малого пути без
столкновений считаем достоверным
 ,
откуда следует
,
откуда следует
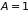 и искомая вероятность
и искомая вероятность
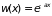 (2.23)
(2.23)
Согласно определению, средняя длина свободного пробега есть
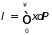 ,
,
где
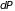 – вероятность столкновения на интервале
(
– вероятность столкновения на интервале
(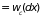 )
после безстолкновительного прохождения
расстояния
(
)
после безстолкновительного прохождения
расстояния
(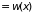 ),
т.е.
),
т.е.
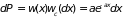 .
.
Интегрирование дает
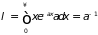 .
.
Таким образом, вероятность того, что молекула пролетит путь , не испытав ни одного столкновения, равна
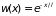 . (2.24)
. (2.24)
Данное распределение является функцией средней длины свободного пробега и не зависит от координат места последнего столкновения. Это означает, что расстояние отсчитывается от произвольной точки, а не от места последнего столкновения. Полученная формула лежит в основе экспериментального определения средней длины свободного пробега молекул в газе.
|
Представим
себе узкий направленный пучок молекул,
входящий в некоторый откачанный до
низкого давления сосуд с двумя
охлаждаемыми полупрозрачными пластинами
(решетки), помещенными на расстояниях
|
Рис. 2.6. |
пролетевшие путь
и
без соударений, оседают на пластинах в
виде слоев. Путем измерения их толщин
(пропорциональных плотности частиц,
осевших на пластине) определяется
отношение числа частиц на пластинах
и
.
Учитывая, что
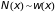 и формулу (2.24) находим среднюю длину
свободного пробега из соотношения
и формулу (2.24) находим среднюю длину
свободного пробега из соотношения
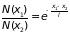 .
.
По порядку величины
составляет около 10 см при
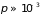 мм. рт. ст.
и около
мм. рт. ст.
и около
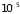 см
при атмосферном давлении.
см
при атмосферном давлении.
2.7. Идеальный газ во внешнем поле
2.7.1. Распределение
Больцмана. При помещении газа во
внешнее поле каждая молекула помимо
кинетической приобретает еще и
потенциальную энергию, которая в общем
случае является функцией координат
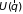 :
:
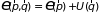 .
.
Подстановка
суммарной энергии в каноническое
распределение Гиббса определяет
вероятность того, что молекула имеет
значение импульса
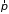 и находится в окрестности точки с
радиус-вектором
и находится в окрестности точки с
радиус-вектором
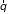 :
:
 .
.
Здесь интегрирование ведется по всем возможным значениям переменных.
Поскольку кинетическая энергия молекулы идеального газа зависит от импульса, а потенциальная от координат, последнюю формулу можно представить двумя сомножителями
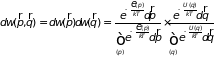 .
.
Первый
из множителей – ранее полученное
распределение Максвелла. Второй –
вероятность нахождения молекулы в
элементе объема
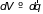 ,
которая зависит от потенциальной энергии
молекулы во внешнем поле. Когда внешнее
поле отсутствует последний множитель
сводится к отношению
.
Распределение молекул в пространстве
в поле внешних сил
,
которая зависит от потенциальной энергии
молекулы во внешнем поле. Когда внешнее
поле отсутствует последний множитель
сводится к отношению
.
Распределение молекул в пространстве
в поле внешних сил
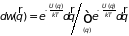 (2.25)
(2.25)
называют распределением Больцмана.
На основе теореме умножения вероятностей указанное распределение можно рассматривать как произведение вероятности двух независимых событий. Это обстоятельство выражает не очевидное важное свойство молекул идеального газа: значение ее импульса совершенно не зависит от ее положения в пространстве. Распределение молекул по импульсам (или скоростям) не изменяется от того, находится ли газ в поле внешних сил или нет. Независимость распределения молекул по координатам и импульсам позволяет рассматривать каждое из них в отдельности.
2.7.2. Идеальный
газ в гравитационном поле. Применим
распределение Больцмана к газу, который
находится в гравитационном поле (земного
тяготения). Направим ось
вертикально вверх. Тогда потенциальная
энергия газовой молекулы массы
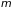 будет равна
будет равна
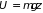 .
Поскольку
.
Поскольку
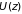 зависит только от высоты, в плоскости
зависит только от высоты, в плоскости
 молекулы распределены равномерно.
Интерес представляет лишь зависимость
распределения вероятностей от координаты
молекулы распределены равномерно.
Интерес представляет лишь зависимость
распределения вероятностей от координаты
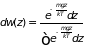 (2.26)
(2.26)
где
интеграл берется по всем возможным
значениям
.
Вводя вместо распределения вероятностей
среднее число частиц в единице объема
(плотность)
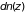 на данной высоте последнюю формулу
можно переписать в виде
на данной высоте последнюю формулу
можно переписать в виде
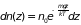 (2.27)
(2.27)
где
 – плотность частиц на условном уровне
отсчета координаты, например, в плоскости
– плотность частиц на условном уровне
отсчета координаты, например, в плоскости
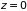 .
Формула показывает, что плотность газа
в поле тяжести убывает по экспоненциальному
закону. Она уменьшается в
.
Формула показывает, что плотность газа
в поле тяжести убывает по экспоненциальному
закону. Она уменьшается в
 раз на характеристической длине
распределения частиц в поле тяжести
раз на характеристической длине
распределения частиц в поле тяжести
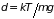 (для газов
(для газов
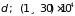 м). На всех высотах имеет место
максвелловское распределение по
скоростям с постоянной температурой
.
м). На всех высотах имеет место
максвелловское распределение по
скоростям с постоянной температурой
.
На первый взгляд
может показаться, что температура с
высотой меняется. Когда молекула
поднимается вверх, ее потенциальная
энергия
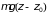 увеличивается и должна меняться
кинетическая энергия
увеличивается и должна меняться
кинетическая энергия
 .
.
Но кинетическая
энергия связана со скоростью молекулы.
Поэтому на большей высоте молекула
будет иметь меньшую скорость и энергию.
А температура определяется средней
квадратичной скоростью (см. п. 2.4.3)
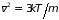 .
Следовательно, температура должна
уменьшаться с высотой. Ошибочность
этого рассуждения коренится в том, что
в нем фигурирует только одна молекула,
рассматриваемая без учета ее столкновений
с другими молекулами. Максвелловское
распределение скоростей устанавливается
благодаря столкновениям. Здесь
столкновительный процесс полностью
игнорируется и рассматривается не
имеющая смысла «температура молекулы».
Фактически подниматься вверх будут
преимущественно те молекулы, которые
имеют большую скорость, и максвелловское
распределение устанавливается
автоматически на всех высотах.
.
Следовательно, температура должна
уменьшаться с высотой. Ошибочность
этого рассуждения коренится в том, что
в нем фигурирует только одна молекула,
рассматриваемая без учета ее столкновений
с другими молекулами. Максвелловское
распределение скоростей устанавливается
благодаря столкновениям. Здесь
столкновительный процесс полностью
игнорируется и рассматривается не
имеющая смысла «температура молекулы».
Фактически подниматься вверх будут
преимущественно те молекулы, которые
имеют большую скорость, и максвелловское
распределение устанавливается
автоматически на всех высотах.
Определим
распределение по высоте молекул,
обладающих различной массой. Чем больше
масса молекулы, тем быстрее убывает их
число с высотой (2.27). Если число молекул
с массами
и
на высоте
одинаково
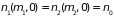 ,
то отношение числа молекул обоих сортов
на высоте
равно
,
то отношение числа молекул обоих сортов
на высоте
равно
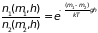 . (2.28)
. (2.28)
Отношение означает, что доля более тяжелых молекул в равновесном газе увеличивается по мере приближения к центру гравитации.
2.7.3. Вес
и потенциальная энергия. Найдем вес
газа, который находится в сосуде –
цилиндре высотой
и площадью основания
.
Можно поступить двояким образом.
Во-первых, считать вес столба газа равным
весу всех входящих в него молекул,
во-вторых, найти разность давлений,
оказываемых газом на дно (
)
и крышку (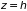 )
сосуда. В первом случае имеем
)
сосуда. В первом случае имеем
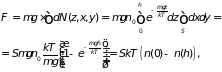 (2.29)
(2.29)
где
площадь сечения сосуда, а
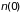 и
и
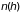 – плотности газа на высоте
и
,
соответственно. Во втором случае,
используя уравнение состояния газа
– плотности газа на высоте
и
,
соответственно. Во втором случае,
используя уравнение состояния газа
 ,
можно записать
,
можно записать
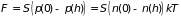 ,
,
где
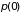 и
и
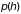 – давления на соответствующих высотах.
Последние выражения совпадают, что
означает: вес газа суть разность давлений
на дно и крышку сосуда. В этом заключается
различие между весом газа и весом тела,
лежащем на тарелке весов.
– давления на соответствующих высотах.
Последние выражения совпадают, что
означает: вес газа суть разность давлений
на дно и крышку сосуда. В этом заключается
различие между весом газа и весом тела,
лежащем на тарелке весов.
Молекулы газа в поле тяжести обладают некоторой средней потенциальной энергией, избыточной по сравнению с энергией газа в отсутствие внешних сил. Средняя потенциальная энергия газовой молекулы в поле тяжести равна
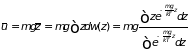 . (2.30)
. (2.30)
Результат вычисления
существенно зависит от высоты столба
газа. Если высота значительно больше
характеристической длины распределения
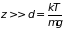 ,
то пределы интегрирования по
распространяются от
до
,
то пределы интегрирования по
распространяются от
до
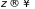 и
и
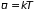 .
.
Средняя потенциальная энергия одной молекулы в бесконечном столбе газа оказывается пропорциональна температуре. Средняя потенциальная энергия грамм-моля газа в бесконечном столбе равна
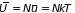 ,
,
т.е. сравнима со
средней кинетической энергией (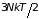 ).
).
Иной результат
получается для сосуда с малой высотой
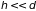 .
Показатель экспоненты в исходной формуле
очень мал
.
Показатель экспоненты в исходной формуле
очень мал
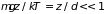 ,
и подынтегральную функцию можно разложить
в ряд, ограничившись первым членом
разложения:
,
и подынтегральную функцию можно разложить
в ряд, ограничившись первым членом
разложения:
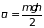 ;
;
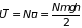 .
.
В этом приближении средняя потенциальная энергия столба газа вообще не зависит от температуры.
Сопоставление свойств идеального газа и земной атмосферы показали на их существенное несоответствие: состав атмосферы не меняется с высотой, как это следует из формулы (2.28). Общеизвестно понижение температуры с увеличением высоты, что противоречит требованиям постоянства температуры.
Эти противоречия ставят два вопроса: 1) правильны ли были основные положения теории; 2) если да, то применимы ли полученные закономерности к явлениям, происходящем в атмосфере. На первый вопрос должен, без сомнения, следовать положительный ответ. Поскольку изложенная теория равновесного идеального газа получила подтверждение в газовых законах, при экспериментальной проверке распределения Максвелла, длины свободного пробега и т.п. Что касается второго вопроса, то ответ – отрицательный. Земная атмосфера не является адекватной моделью равновесного газа. Земная атмосфера явно система неравновесная; явления, происходящие в ней, весьма сложные: это и конвекционные потоки, солнечное излучение, механическое перемешивание слоев, связанное с движением Земли, и другие осложняющие факторы.



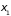 и
и
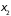 от входного отверстия (Рис.
2.6). Молекулы,
от входного отверстия (Рис.
2.6). Молекулы,