4.7. Зависимость энергии электрона от волнового вектора. Эффективная масса

4.7.1. Дисперсионное уравнение электрона в металле. Дуализм частиц и волн в квантовой механике позволяет сформулировать полученные ранее результаты для электронов-частиц на языке волн. Согласно соотношению де Бройля, волновой и корпускулярный аспекты электрона связаны между собой 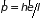. Здесь 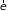– единичный вектор в направлении движения электрона, 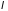– его длина волны. Вводится волновой вектор 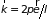, который определяет длину волны в направлении движения электрона и его импульс 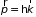. Тогда кинетическая энергия электрона может быть записана в виде

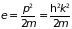. (4.36)

Отсюда максимальная энергия при абсолютном нуле температуры (энергия Ферми ) определяет и максимальную величину вектора :

.

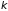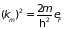Энергия – квадратичная функция , так что в пространстве , , 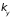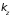уравнение 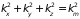определяет сферу, на поверхности которой энергия электрона принимает максимальное значение. Указанная сфера носит название сферы Ферми, а ее поверхность – поверхность Ферми для свободных электронов. Естественно, при взаимодействии электронов с ионным остовом поверхность Ферми не будет сферой, принимает различные формы.

Решение уравнения Шредингера для свободного электрона, двигающегося вдоль оси , (4.35) – плоская бегущая волна 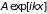. Его подстановка в (4.35) определяет дисперсионное уравнение 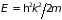. Квадрат модуля волновой функции пропорционален вероятности обнаружения электрона в интервале между и 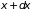. Поскольку в нашем случае 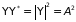, то нахождение электрона в любой точке пространства имеет равную вероятность.

Вероятность обнаружения электрона, движущегося в периодическом поле ионного остова, должна быть периодической функцией координаты . Это означает, что амплитуда волновой функции 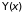не остается постоянной, как у свободного электрона, а периодически меняется, т.е. модулирована с периодом, равным постоянной решетки:

,

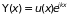здесь 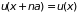, где – любое целое число. Конкретное выражение функции зависит от потенциальной энергии 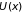, входящей в уравнение Шредингера (4.34). Указанное решение приводит к следующему дисперсионному уравнению

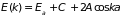, (4.37)

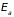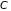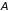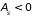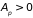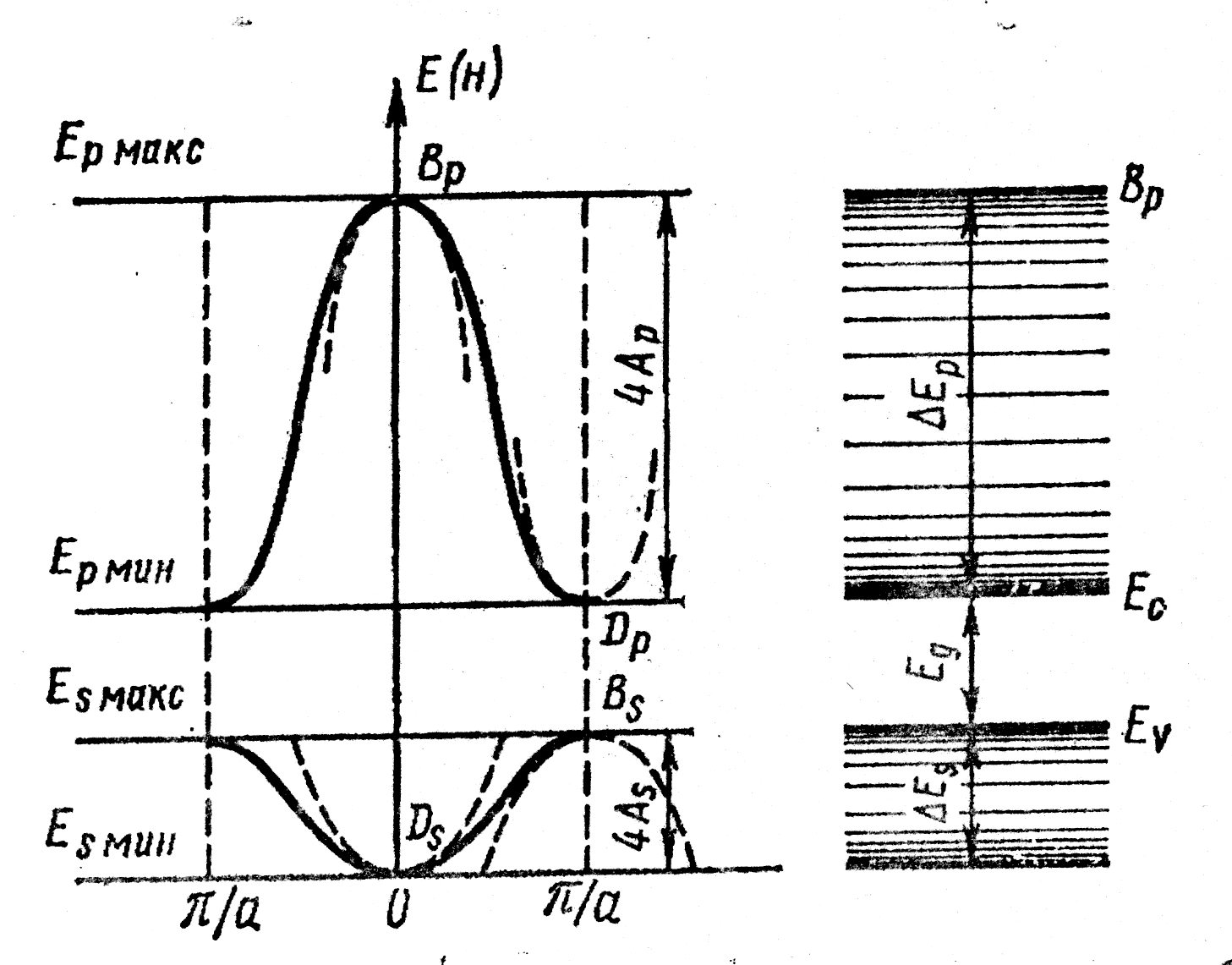
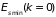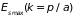где – энергия атомного уровня, из которого образовалась зона, – сдвиг этого уровня под действием поля соседних атомов, – обменный интеграл, учитывающий возможность перехода электрона от атома к атому (за счет перекрытия их волновых функций). Для -состояний , для -состояний . На рис. 4.6 показаны зависимости для - и -зон. Ширина разрешенной -зоны от до равна 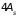, 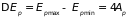. Чем выше располагается атомный уровень, тем шире соответствующая энергетическая зона. Область значений волнового вектора, в пределах которой энергия электрона испытывает полный цикл своего изменения, называют зонами Бриллюэна. Для одномерного кристалла первая зона Бриллюэна простирается от 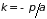до 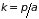. Минимум дисперсионной кривой называют дном энергетической зоны, максимум – вершиной или потолком зоны. Ранее было отмечено, что кинетические явления в металле обусловлены электронами, которые занимают энергетические подуровни вблизи вершины или дна зоны проводимости. Речь идет об области экстремумов дисперсионной кривой, т.е. вблизи точек 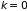и 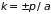(середина и граница первой зоны Бриллюэна) (Рис. 4.6). 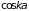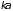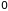После разложения в ряд по ( отсчитывается от для середины зоны и от 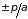для границы зоны, соответственно, 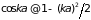и 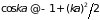), получим

Рис. 4.6

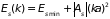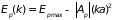; . (4.38)

Таким образом, у дна и вершины энергетической зоны энергия электрона пропорциональна ширине зоны и квадрату волнового вектора. Полученные соотношения удобно переписать в более общем виде для дна и потолка зоны:

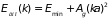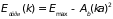; . (4.39)

Совпадение характера зависимостей для электронов в кристалле, участвующих в кинетических явлениях, и свободных является еще одним аргументом в пользу модели свободных электронов в металлах.

4.7.2. Эффективная масса электрона. Скорость и ускорение поступательного движения электрона с учетом формулы де Бройля ( ) определяются известными соотношениями

, .

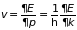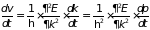Поскольку импульс в единицу времени есть сила, действующая на электрон 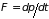, то ускорение оказывается равным

.

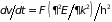Формула устанавливает связь между ускорением электрона и внешней силой , действующей на него со стороны внешнего поля. Из нее следует, что электрон под действием внешней силы движется в среднем как свободный, если бы он обладал массой

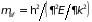, (4.40)

которую называю эффективной. Она отражает все особенности движения электрона в периодическом поле кристалла, является весьма своеобразной величиной, а именно: может быть как положительной, так и отрицательной, во много раз большей или меньшей массы покоя электрона. Так, например, подставляя в последнюю формулу выражения (4.39), получаем эффективные массы электронов, располагающиеся у дна и потолка зоны, соответственно

; .

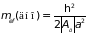В первом случае эффективная масса положительная, а во втором – отрицательная. Электроны с 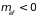ведут себя аномально: они ускоряются в направлении, противоположном действию внешней силы.

Для свободного электрона вся работа внешней силы 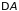идет на увеличение кинетической энергии поступательного движения, т.е. 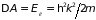. Подставляя 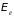в (4.40), получим, что эффективная масса свободного электрона равна его массе покоя, 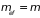. Иная ситуация имеет место для электрона в кристалле: он обладает не только кинетической, но и потенциальной энергией. Поэтому энергия внешнего источника переходит частично как в кинетическую (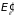 ), так и потенциальную ( ) энергию: 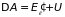. В этом случае кинетическая энергия, а следовательно, и скорость движения электрона будут возрастать медленнее, чем у свободного электрона. Электрон становится как бы тяжелее, 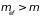. Если вся работа внешних сил переходит в потенциальную энергию 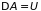, то приращения кинетической энергии и скорости движения электрона не будет – электрон ведет себя как частица с бесконечно большой эффективной массой: 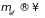. Когда в потенциальную энергию переходит не только энергия внешней силы, но и часть кинетической энергии электрона 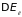, так что 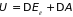, то скорость такого электрона в кристалле уменьшается, он замедляется, что характерно для частиц с отрицательной эффективной массой . Переход в кинетическую энергию внешней работы и части потенциальной энергии 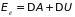приводит к тому, что скорость растет быстрее, чем у свободного электрона. Он становится легче свободного электрона, т.е. .

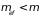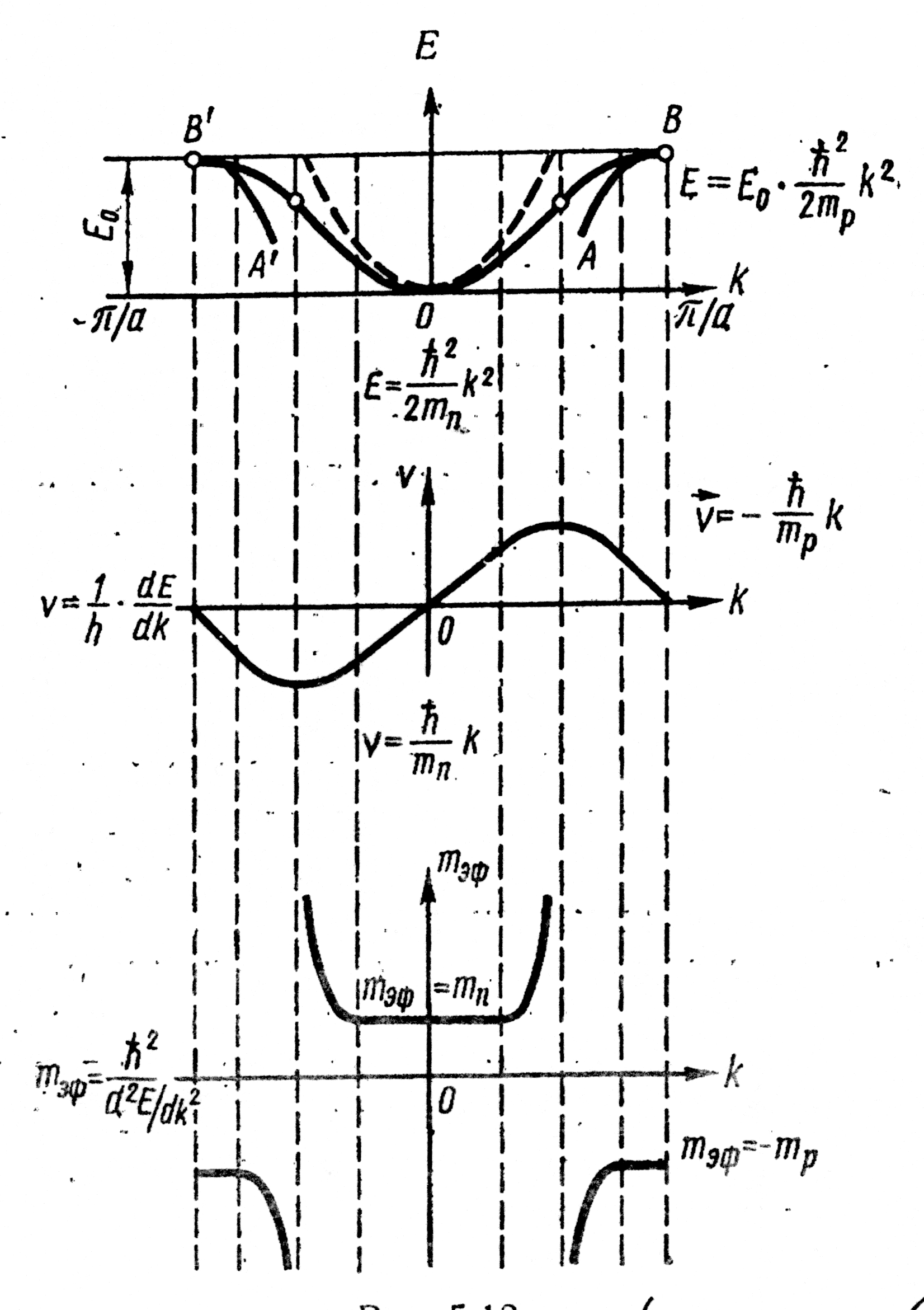
Отмеченная динамика инертных свойств электрона иллюстрируется рис. 4.7, на котором показан характер изменения полной энергии электрона , скорости его поступательного движения 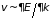и эффективной массы 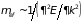с возрастанием волнового вектора от до . У дна зоны (вблизи ) растет пропорционально 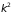, скорость пропорциональна , эффективная масса сохраняет постоянное положительное значение. В точке перегиба кривой первая производная (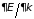 ), а следовательно, абсолютное значение скорости достигает максимума (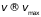 ), а эффективная масса , поскольку . 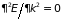За точкой перегиба скорость убывает, что при сохранившемся направлении действия внешней силы эквивалентно изменению знака эффективной массы с положительного на отрицательный. У вершины зоны становится квадратичной функцией и эффективная масса достигает постоянного отрицательного значения.

Рис. 4.7