3.2. Второе начало термодинамики

3.2.1. Статистический смысл энтропии. Абсолютную постоянную в формуле (3.7) выберем за начало отсчета:

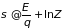. (3.12)

В равновесной макроскопической системе вероятность состояний с энергией, совпадающей со средней 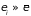, почти равна единице. Поэтому наибольший вклад в функцию состояния вносит то слагаемое, которое относится к средней энергии. Пренебрегая близкой к нулю суммой остальных слагаемых, имеем:

.

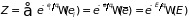Обращаясь к формуле (3.12), находим

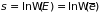. (3.13)

Энтропия макроскопической квазизамкнутой системы оказывается равной логарифму числа состояний, отвечающих средней энергии системы, то есть логарифму числа состояний равновесной системы. Таким образом, энтропия идентична функции, введенной при выводе распределения Гиббса.

Энтропия сложной системы, состоящей из независимых подсистем равна

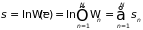. (3.14)

Такое равенство можно получить и из формулы (3.12). Отсюда следует важное свойство энтропии – её аддитивность. Степень достоверности такого утверждения такая же, как утверждения об аддитивности энергии.

3.2.2. Формула Больцмана. Представим неравновесную систему как совокупность большого числа подсистем. Их число зависит от времени наблюдения: чем меньше подсистема, тем меньше у нее время релаксации. Деление системы проведем таким образом, чтобы время наблюдения было больше времени релаксации каждой из подсистем. Тогда последние можно рассматривать как равновесные и для них по-прежнему справедлива формула (3.13). Здесь уже не предполагается, что между отдельными частями системы существует равновесие: отдельные подсистемы находятся в равновесном состоянии, но каждая из них характеризуется своими параметрами и распределением вероятностей. Учитывая аддитивность энтропии, получим

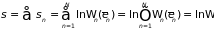. (3.15)

Если для равновесной системы полное число состояний 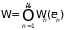определяется средним значением энергии 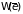, то для неравновесной – .

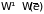Используя микроканоническое распределение в замкнутой системе , получаем формулу Больцмана:

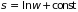(3.16)

– основу статистического толкования термодинамики. Она связывает значение энтропии замкнутой системы с вероятностью её состояния.

3.2.3. Закон возрастания энтропии. Изменение энтропии замкнутой системы при переходе из одного состояния в другое равно

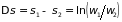, (3.17)

где 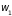и – вероятности первого и второго состояний. Пусть – вероятность начального неравновесного состояния. Через некоторое время система благодаря слабому взаимодействию между её частями, перейдет из неравновесного состояния в равновесное, и энтропия увеличится (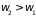 ). Таким образом, согласно (3.17), возрастание энтропии замкнутой системы связано с переходом её из менее вероятного состояния в более вероятное. Наибольшее значение она принимает в состоянии статистического равновесия.

Переход системы в равновесное состояние совершается монотонно, через последовательность всё более и более вероятных состояний, и энтропия системы всё время возрастает. Если же система уже находилась в состоянии статистического равновесия, то её энтропия сохраняет неизменное максимальное значение (Рис. 3.1). Это и составляет содержание второго начала термодинамики. Его можно сформулировать следующим образом:

Наиболее вероятным ходом процессов в замкнутой макроскопической системе является такой, при котором её энтропия возрастает или остается постоянной:

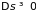, (3.18)

где знак неравенства относится к процессам, приближающим систему к равновесному состоянию, а знак равенства – к процессам, которые происходят в системе, уже находящейся в состоянии равновесия.

	Формулировка второго начала феноменологической термодинамики более категорична, отсутствуют слова «наиболее вероятный». Статистическая термодинамика допускает и наличие процессов с уменьшением энтропии, но рассматривает их как маловероятные. Изменение или постоянство энтропии можно
Рис. 3.1.

считать критерием обратимости и необратимости процессов. При необратимых процессах энтропия увеличивается 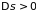(система подходит к состоянию равновесия), при обратимых – остается постоянной .

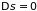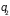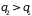Примером необратимого процесса в замкнутой системе служит обмен энергией между двумя ее частями, находящимися при разных температурах, и ( ). Для замкнутой системы с учетом аддитивности энтропии из второго начала следует

.

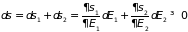Поскольку 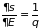и система замкнута 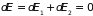, то

.

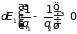Это доказывает, что менее нагретая часть получает от второй энергию 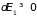, т.е. тепло переходит от более нагретой к менее нагретой части системы.

Полученный закон возрастания энтропии замкнутых систем обобщим на случай незамкнутых систем. Среди них выделим теплоизолированные системы, взаимодействие которых с окружением осуществляется через внешние поля. Но изменение внешних полей не может привести к изменению числа возможных состояний или распределения по состояниям. Поэтому переход из менее вероятных состояний в более вероятные происходит по тем же законам, что и для замкнутой системы, то есть .

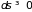Для произвольных незамкнутых систем можно рассуждать следующим образом. При контакте с окружающей средой система получает (отдает) некоторое количества тепла , которое изменяет энтропию на величину 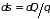. Процесс же перехода из менее вероятного состояния в более вероятное сохраняется, только в этом случае возрастание энтропии происходит на величину, избыточную по сравнению с :

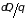. (3.19)

Знак равенства относится к квазистатическому процессу. Для теплоизолированной системы , и (3.19) переходит в неравенство (3.18), справедливое для замкнутых систем. Если в формуле (3.5) учесть (3.19), то получим основное термодинамическое неравенство

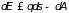, (3.20)

справедливое для произвольных процессов в незамкнутых системах. Здесь знак равенства относится к обратимым процессам, а неравенства – к необратимым. Формула (3.20) объединяет запись закона сохранения энергии и закона возрастания энтропии и может быть названа объединенной формой записи первого и второго начал термодинамики.

Отношение , согласно (3.6), есть полный дифференциал, поэтому энтропия представляет собой однозначную функцию состояния системы, которая удовлетворяет условию

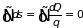. (3.21)

Температуру с математической точки зрения можно рассматривать как интегрирующий делитель выражения . В дальнейшем мы будем использовать термодинамическую энтропию , которая связана со статистической соотношением 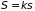, где – постоянная Больцмана.