- •1. Основные положения статистической термодинамики
- •1.1. Понятия и начала феноменологической термодинамики.
- •1.2. Микроскопическое (механическое) описание классических систем.
- •1.3. Особенности представления квантовых систем
- •1.4. Вероятность нахождения системы в элементе фазового пространства. Метод ансамблей Гиббса.
- •1.5. Макроскопические величины как фазовые средние
- •1.6. Распределение в системах с постоянным числом частиц
- •1.6.2. Распределения Гиббса.
- •1.6.3. Квазиклассическое приближение.
- •1.7. Свойства распределения Гиббса
- •1.8. Большое каноническое распределение Гиббса
- •2. Статистика идеального газа
- •2.1. Идеальный газ как модель статистической системы
- •2.2. Распределение Максвелла
- •2.3. Столкновения молекул со стенкой сосуда. Давление
- •2.4. Характерные величины идеального газа
- •2.5. Столкновение молекул между собой
- •2.6. Длина свободного пробега
- •2.7. Идеальный газ во внешнем поле
- •2.8. Число и функция состояний идеального газа
- •2.9. Классическая теория теплоемкости газа двухатомных молекул
- •2.10. Квантовая теория теплоемкости газа двухатомных молекул
- •2.11. Распределения в квантовых системах
- •3. Законы термодинамики
- •3.1. Статистическое обоснование первого начала термодинамики
- •3.2. Второе начало термодинамики
- •3.3. Вечный двигатель второго рода. Максимальная работа процессов
- •3.4. Полезная работа тепловых машин
- •3.5. Метод термодинамических потенциалов
- •3.6. Термодинамические коэффициенты. Критерии устойчивости равновесия
- •3.7. Статистическое вычисление термодинамических величин
- •3.8. Третье начало термодинамики (теорема Нернста)
- •3.9. Применения термодинамики
- •4. Статистика сложных систем.
- •4.1. Модель кристаллического твердого тела. Уравнение движения атомов
- •4.2. Дисперсионное уравнение нормальных колебаний кристалла
- •4.3. Кристалл как система линейных гармонических осцилляторов
- •4.4. Статистическая сумма и энергия кристалла (в гармоническом приближении)
- •4.5. Теория теплоемкости Дебая
- •4.6. Электронный газ в металлах
- •4.7. Зависимость энергии электрона от волнового вектора. Эффективная масса
- •4.8. Теория парамагнетизма. Природа и характеристики магнетизма.
- •4.9. Равновесное излучение.
- •4.10. Системы с кулоновским взаимодействием частиц.
- •5. Теория малых флуктуаций
- •5.1. Определение и значение флуктуаций
- •5.2. Мера вероятности и масштаб флуктуаций
- •5.3. Флуктуации термодинамических величин в однородной среде
- •5.4. Предельная чувствительность измерительных приборов
- •5.5. Рассеяния света флуктуациями
- •6. Элементы теории физической кинетики
- •6.1. Определения и характеристики необратимых процессов
- •6.2. Теория стационарных процессов в газе свободных электронов
- •6.3. Газокинетическое уравнение Больцмана
- •6.4. Приближение времени релаксации
- •Раздел 2
- •Раздел 2
- •Раздел 3
- •Раздел 4
- •Раздел 5
- •Раздел 6
- •Список Литературы
6.3. Газокинетическое уравнение Больцмана
6.3.1. Приближение
Больцмана. Основные
проблемы молекулярно-кинетической
теории неравновесных процессов – это,
во-первых, нахождение уравнений,
определяющих изменение функций
распределения в пространстве и во
времени, и, во-вторых, установление
связей между нею и макроскопическими
величинами (потоками). Заметим, что при
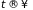 неравновесные функции распределения
должны в пределе переходить в равновесные,
если отсутствуют внешние воздействия.
Кинетический подход к изучению
неравновесных явлений является более
глубоким и должен давать обоснование
формальным методам неравновесной
термодинамики.
неравновесные функции распределения
должны в пределе переходить в равновесные,
если отсутствуют внешние воздействия.
Кинетический подход к изучению
неравновесных явлений является более
глубоким и должен давать обоснование
формальным методам неравновесной
термодинамики.
Состояние
одноатомного газа в неравновесном
состоянии характеризуется совокупностью
изобразительных точек в шестимерном
-пространстве,
перемещающихся по своим фазовым
траекториям. Плотность изобразительных
точек (функция распределения) в
-пространстве
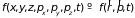 неравновесной системы зависит от времени
как явно, так и через координаты
неравновесной системы зависит от времени
как явно, так и через координаты
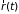 и импульса
и импульса
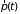 .
Плотность числа частиц в координатном
.
Плотность числа частиц в координатном
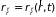 и импульсном
и импульсном
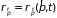 пространствах связаны с функцией
распределения соотношениями
пространствах связаны с функцией
распределения соотношениями
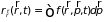 ;
;
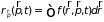 .
.
Нахождения
функции распределения и ее зависимости
от координат и времени – центральная
задача физической кинетики. Знание
функции
 позволяет решить широкий класс задач,
относящихся к неравновесным состояниям
системы. К ним относятся явления
релаксации, определения кинетических
коэффициентов в процессах переноса
(электропроводность, теплопроводность,
диффузия и т.д.). Пусть, например,
– некая аддитивная физическая величина,
отнесенная к одной молекуле (энергия,
импульс и т.д.). Тогда выражения
позволяет решить широкий класс задач,
относящихся к неравновесным состояниям
системы. К ним относятся явления
релаксации, определения кинетических
коэффициентов в процессах переноса
(электропроводность, теплопроводность,
диффузия и т.д.). Пусть, например,
– некая аддитивная физическая величина,
отнесенная к одной молекуле (энергия,
импульс и т.д.). Тогда выражения
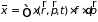 ;
;
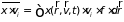
представляют собой
пространственную плотность и плотность
потока для макроскопической величины
(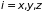 ).
Здесь должно быть учтено условие
нормировки
).
Здесь должно быть учтено условие
нормировки
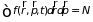 ,
где
– полное число частиц газа.
,
где
– полное число частиц газа.
Если в равновесном состоянии существует универсальное распределение Гиббса, то в неравновесных состояниях индивидуальные особенности той или иной системы и многообразие внешних воздействий на нее сказываются настолько сильно, что никакой универсальной формулы для функции распределения получить не удается. Более того, даже уравнение, описывающее пространственную и временную зависимость функции распределения (кинетическое уравнение) можно определить только в некоторых предельных случаях при более или менее далеко идущих предположениях.
В классической кинетике существует два подхода к анализу неравновесных процессов; один из них пригоден для описания явлений в разреженных газах (метод кинетического уравнения Больцмана), а другой – для описания плотных газов (уравнение Смолуховского, Фоккера-Планка).
|
а) б) |
Рис. 6.5 |
Допустим,
что газ нейтральных молекул настолько
разрежен, что длина свободного пробега
много больше радиуса действия
межмолекулярных сил
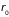 (сечения соударения
(сечения соударения
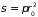 )
и соответственно время свободного
пробега
много больше времени взаимодействия
двух молекул
)
и соответственно время свободного
пробега
много больше времени взаимодействия
двух молекул
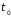 .
Так как
.
Так как
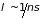 ,
где
– плотность числа молекул, то критерий
применения уравнения Больцмана имеет
вид
,
где
– плотность числа молекул, то критерий
применения уравнения Больцмана имеет
вид
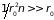 или
или
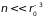 .
Поскольку
.
Поскольку
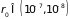 см, то
см, то
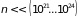 см–3.
В этом случае можно ввести понятие
«столкновение» молекул, понимая под
этим процесс изменения параметров
движения одной молекулы за то время,
которая она проводит в сфере действия
другой. В силу неравенства
см–3.
В этом случае можно ввести понятие
«столкновение» молекул, понимая под
этим процесс изменения параметров
движения одной молекулы за то время,
которая она проводит в сфере действия
другой. В силу неравенства
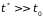 предполагается процесс столкновения
мгновенным. Изменение координат молекул
за время столкновения
предполагается процесс столкновения
мгновенным. Изменение координат молекул
за время столкновения
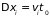 можно считать равным нулю, но изменение
проекции скорости и импульса молекулы
можно считать равным нулю, но изменение
проекции скорости и импульса молекулы
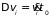 и
и
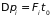 имеет конечное значение. Таким образом,
в этом приближении столкновение
сопровождается лишь скачкообразным
изменением импульса обеих молекул.
Характер движения в рассматриваемом
приближении иллюстрирует рис. 6.5а. В
момент столкновения изобразительная
точка молекулы в фазовом
-пространстве
скачком переходит из одного положения
в другое. В силу этого уравнение
непрерывности для функции распределения
несправедливо. Это значит, что в
-пространстве
существуют источники и стоки функции
распределения, мощность которых
определяется столкновениями между
молекулами.
имеет конечное значение. Таким образом,
в этом приближении столкновение
сопровождается лишь скачкообразным
изменением импульса обеих молекул.
Характер движения в рассматриваемом
приближении иллюстрирует рис. 6.5а. В
момент столкновения изобразительная
точка молекулы в фазовом
-пространстве
скачком переходит из одного положения
в другое. В силу этого уравнение
непрерывности для функции распределения
несправедливо. Это значит, что в
-пространстве
существуют источники и стоки функции
распределения, мощность которых
определяется столкновениями между
молекулами.
В альтернативном
предельном случае
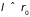 ,
,
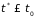 характер движения иллюстрирует рис.
6.5б. Очевидно, в случае плотных газов
(
характер движения иллюстрирует рис.
6.5б. Очевидно, в случае плотных газов
(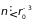 )
понятие «столкновение» теряет смысл,
так как молекула все время находится
внутри сферы действия соседних молекул.
)
понятие «столкновение» теряет смысл,
так как молекула все время находится
внутри сферы действия соседних молекул.
6.3.2. Уравнение
непрерывности в отсутствие столкновений.
Перейдем к изучению
процессов в разреженных газах (приближение
Больцмана, учитываются только попарные
столкновения). Передвигаясь по фазовым
траекториям, изобразительные точки
распределены в
-пространстве
с плотностью
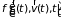 .
В последующий момент времени
.
В последующий момент времени
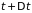 функция распределения примет значение
функция распределения примет значение
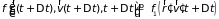 .
Выберем промежуток времени
значительно большим, чем время столкновения
(
.
Выберем промежуток времени
значительно большим, чем время столкновения
(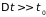 ).
С другой стороны считаем
малым по сравнению со средним временем
между столкновениями (
).
С другой стороны считаем
малым по сравнению со средним временем
между столкновениями (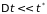 ),
т.е. путь, пройденный частицей за это
время будет намного меньшим, чем средняя
длина свободного пробега. Иными словами,
характер движения частицы в этот
промежуток времени определяется
координатами
),
т.е. путь, пройденный частицей за это
время будет намного меньшим, чем средняя
длина свободного пробега. Иными словами,
характер движения частицы в этот
промежуток времени определяется
координатами
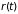 ,
скоростью
,
скоростью
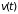 в предыдущий момент времени и внешними
силами
в предыдущий момент времени и внешними
силами
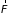 :
:
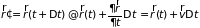 ;
;
 .
.
Здесь предполагается,
что система однородная, а сила
не зависит от координат пространства.
В этих условиях число изобразительных
точек в элементе объема
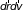 не меняется, т.е.
не меняется, т.е.
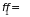 .
Представляя
.
Представляя
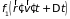 в виде ряда
в виде ряда
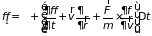 ,
,
приходим к уравнению непрерывности, которое определяет дрейфовую производную
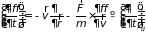 . (6.19)
. (6.19)
Второе слагаемое в правой части уравнения отлично от нуля только в том случае, если газ помещен во внешнее поле.
6.3.3. Учет
столкновительных процессов.
Столкновения между
молекулами приводят к скачкообразному
изменению проекций скорости (при
неизменных координатах) и, следовательно,
к скачкообразному перемещению
изобразительных точек. В этом приближении
они «гибнут» в одних частях
-пространства
и «рождаются» в других не пересекая
границ выделенного объема
.
Это значит, что приближение «мгновенных»
столкновений вынуждает ввести в правую
часть уравнения непрерывности источники
и стоки молекул данной скорости в данной
точке пространства. Поэтому общее
изменение функции
во времени можно представить суммой
дрейфовой и столкновительной
производных
 .
А (6.19) должно быть заменено уравнением
.
А (6.19) должно быть заменено уравнением
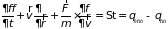 , (6.20)
, (6.20)
где
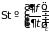 называют еще и интегралом столкновений
(stoss
integral),
а величины
называют еще и интегралом столкновений
(stoss
integral),
а величины
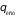 ,
,
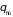 представляют собой мощности источников
и стоков – числа частиц со скоростью
представляют собой мощности источников
и стоков – числа частиц со скоростью
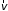 в точке
,
появляющиеся и исчезающие за единицу
времени в единице объема и отнесенные
к единичному интервалу скоростей.
в точке
,
появляющиеся и исчезающие за единицу
времени в единице объема и отнесенные
к единичному интервалу скоростей.
Опишем
физическую основу вычисления
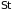 .
Рассмотрим столкновения молекул, из
которых одна имеет скорость в интервале
.
Рассмотрим столкновения молекул, из
которых одна имеет скорость в интервале
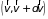 ,
а другая – в интервале
,
а другая – в интервале
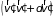 .
После соударения молекулы приобретают
скорости, лежащие в интервалах
.
После соударения молекулы приобретают
скорости, лежащие в интервалах
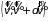 и
и
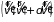 ,
соответственно. Число таких столкновений
за единицу времени в единичном объеме
пропорционально числам сталкивающихся
молекул со скоростями
и интервалам значений скоростей после
удара
,
соответственно. Число таких столкновений
за единицу времени в единичном объеме
пропорционально числам сталкивающихся
молекул со скоростями
и интервалам значений скоростей после
удара
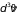 и
и
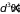 (здесь
(здесь
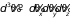 ,
в общем случае
,
в общем случае
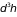 – элементарный объем в соответствующем
фазовом пространстве
– элементарный объем в соответствующем
фазовом пространстве
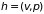 ).
Таким образом, это число можно записать
в виде
).
Таким образом, это число можно записать
в виде
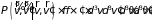 ,
,
где для краткости
обозначено
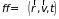 ,
,
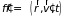 ,
,
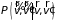 – плотность вероятности соударения
– плотность вероятности соударения
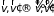 ,
зависящая от скоростей обеих молекул
до и после удара. Полное число соударений,
испытываемых молекулами со скоростями
в интервале
за единицу времени в единице объема,
вычисляется интегрированием по всем
значениям
,
зависящая от скоростей обеих молекул
до и после удара. Полное число соударений,
испытываемых молекулами со скоростями
в интервале
за единицу времени в единице объема,
вычисляется интегрированием по всем
значениям
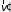 ,
,
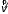 ,
,
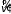 .
При малом интервале
.
При малом интервале
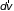 это и определяет убыль числа молекул с
указанными скоростями
.
Таким образом, мощность стоков равна
это и определяет убыль числа молекул с
указанными скоростями
.
Таким образом, мощность стоков равна
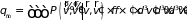 .
.
Наряду
с процессами
,
приводящими к уменьшению числа молекул
со скоростью
,
в газе происходят и обратные процессы
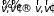 ,
которые увеличивают их число. Они
порождают источники с мощностью
,
которые увеличивают их число. Они
порождают источники с мощностью
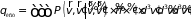 ,
,
где
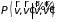 – плотность вероятности перехода
,
– плотность вероятности перехода
,
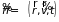 ,
,
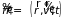 .
Первый аргумент функции распределения
одинаков во всех функциях, т.к. при ударе
координаты в приближении мгновенных
соударений не изменяются. Считая функцию
плотности вероятности соударений
симметричной по отношению к перестановке
аргументов начального и конечного
аргументов
.
Первый аргумент функции распределения
одинаков во всех функциях, т.к. при ударе
координаты в приближении мгновенных
соударений не изменяются. Считая функцию
плотности вероятности соударений
симметричной по отношению к перестановке
аргументов начального и конечного
аргументов
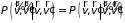 ,
для интеграла столкновений имеем
,
для интеграла столкновений имеем
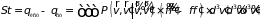 . (6.21)
. (6.21)
Определение функции
можно найти, например, в книгах: Ю.Б.
Румер, М.Ш. Рывкин Термодинамика.
Статистическая физика и кинетика. М.
1972, § 67; Л.В. Радушкевич Курс статистической
физики. М. 1966, § 7. Для классических систем
в предположении, что атомы газа –
абсолютно твердые сферы с диаметрами
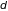
 . (6.22)
. (6.22)
Здесь
– угол между векторами
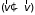 и
и
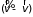 ,
– элемент телесного угла.
,
– элемент телесного угла.
После подстановки (6.21) в (6.20) получаем интегро-дифференциальное уравнение для неравновесной функции распределения
 , (6.23)
, (6.23)
которое называется
кинетическим уравнением Больцмана.
Вывод этого уравнения, идея которого
принадлежит Больцману, нельзя считать
строгим. Здесь предполагается, во-первых,
что изменение по времени функции
аддитивно относительно двух процессов,
имеющих различное происхождение, а
именно: потоки газа вследствие наличия
градиентов плотности и внешних полей
и столкновения. Иными словами,
предполагается, что потоки и соударения
не влияют друг на друга. Во-вторых,
приближение Больцмана учитывает только
попарные столкновения частиц. В третьих,
в интеграле столкновений значения
функций
,
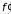 ,
,
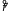 ,
,
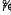 берутся в одной и той же точке пространства
,
в то время как с учетом конечных размеров
молекул координаты в функциях
и
и в функциях
и
должны быть выбраны различными.
берутся в одной и той же точке пространства
,
в то время как с учетом конечных размеров
молекул координаты в функциях
и
и в функциях
и
должны быть выбраны различными.