
- •1. Основные положения статистической термодинамики
- •1.1. Понятия и начала феноменологической термодинамики.
- •1.2. Микроскопическое (механическое) описание классических систем.
- •1.3. Особенности представления квантовых систем
- •1.4. Вероятность нахождения системы в элементе фазового пространства. Метод ансамблей Гиббса.
- •1.5. Макроскопические величины как фазовые средние
- •1.6. Распределение в системах с постоянным числом частиц
- •1.6.2. Распределения Гиббса.
- •1.6.3. Квазиклассическое приближение.
- •1.7. Свойства распределения Гиббса
- •1.8. Большое каноническое распределение Гиббса
- •2. Статистика идеального газа
- •2.1. Идеальный газ как модель статистической системы
- •2.2. Распределение Максвелла
- •2.3. Столкновения молекул со стенкой сосуда. Давление
- •2.4. Характерные величины идеального газа
- •2.5. Столкновение молекул между собой
- •2.6. Длина свободного пробега
- •2.7. Идеальный газ во внешнем поле
- •2.8. Число и функция состояний идеального газа
- •2.9. Классическая теория теплоемкости газа двухатомных молекул
- •2.10. Квантовая теория теплоемкости газа двухатомных молекул
- •2.11. Распределения в квантовых системах
- •3. Законы термодинамики
- •3.1. Статистическое обоснование первого начала термодинамики
- •3.2. Второе начало термодинамики
- •3.3. Вечный двигатель второго рода. Максимальная работа процессов
- •3.4. Полезная работа тепловых машин
- •3.5. Метод термодинамических потенциалов
- •3.6. Термодинамические коэффициенты. Критерии устойчивости равновесия
- •3.7. Статистическое вычисление термодинамических величин
- •3.8. Третье начало термодинамики (теорема Нернста)
- •3.9. Применения термодинамики
- •4. Статистика сложных систем.
- •4.1. Модель кристаллического твердого тела. Уравнение движения атомов
- •4.2. Дисперсионное уравнение нормальных колебаний кристалла
- •4.3. Кристалл как система линейных гармонических осцилляторов
- •4.4. Статистическая сумма и энергия кристалла (в гармоническом приближении)
- •4.5. Теория теплоемкости Дебая
- •4.6. Электронный газ в металлах
- •4.7. Зависимость энергии электрона от волнового вектора. Эффективная масса
- •4.8. Теория парамагнетизма. Природа и характеристики магнетизма.
- •4.9. Равновесное излучение.
- •4.10. Системы с кулоновским взаимодействием частиц.
- •5. Теория малых флуктуаций
- •5.1. Определение и значение флуктуаций
- •5.2. Мера вероятности и масштаб флуктуаций
- •5.3. Флуктуации термодинамических величин в однородной среде
- •5.4. Предельная чувствительность измерительных приборов
- •5.5. Рассеяния света флуктуациями
- •6. Элементы теории физической кинетики
- •6.1. Определения и характеристики необратимых процессов
- •6.2. Теория стационарных процессов в газе свободных электронов
- •6.3. Газокинетическое уравнение Больцмана
- •6.4. Приближение времени релаксации
- •Раздел 2
- •Раздел 2
- •Раздел 3
- •Раздел 4
- •Раздел 5
- •Раздел 6
- •Список Литературы
1.2. Микроскопическое (механическое) описание классических систем.
1.2.1 Уравнения
движения точечных масс (материальных
точек). Рассмотрим движение системы
 материальных точек относительно
некоторой инерциальной системы координат.
Положение и скорость
материальных точек относительно
некоторой инерциальной системы координат.
Положение и скорость
 –ой
материальной точки в данный момент
времени задается ее радиусом-вектором
–ой
материальной точки в данный момент
времени задается ее радиусом-вектором
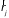 и его производной по времени
и его производной по времени
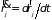 .
В общем случае на материальную точку
действуют силы как со стороны других
материальных точек (внутренние силы),
так и со стороны внешних сил (внешние
силы). Уравнения, описывающие изменения
механического состояния системы во
времени, носят названия уравнения
движения.
.
В общем случае на материальную точку
действуют силы как со стороны других
материальных точек (внутренние силы),
так и со стороны внешних сил (внешние
силы). Уравнения, описывающие изменения
механического состояния системы во
времени, носят названия уравнения
движения.
Для изолированной системы из частиц уравнение движения -ой точки имеет вид
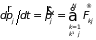 , (1.7)
, (1.7)
где
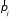 импульс
-ой
частицы,
импульс
-ой
частицы,
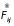
сила, с которой
сила, с которой
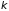 -ая
частица действует на
-ую.
При наличии в системе связей не все
уравнения (1.7) будут независимыми;
существуют ограничения, которые
записываются дополнительными уравнениями
-ая
частица действует на
-ую.
При наличии в системе связей не все
уравнения (1.7) будут независимыми;
существуют ограничения, которые
записываются дополнительными уравнениями
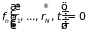 ,
,
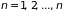 (1.8)
(1.8)
относительно
координат центра масс частиц
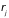 .
Через
.
Через
 обозначено число независимых связей в
системе. Если время
обозначено число независимых связей в
системе. Если время
 не входит в уравнение связи, т.е.
не входит в уравнение связи, т.е.
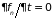 ,
она называется стационарной. Пример
системы с такой связью – две точечные
массы, соединенные стержнем постоянной
длины
,
она называется стационарной. Пример
системы с такой связью – две точечные
массы, соединенные стержнем постоянной
длины
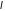 .
В этом случае уравнение связи имеет вид
.
В этом случае уравнение связи имеет вид
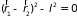 ,
,
или в декартовой системе координат
 .
.
При переменной
длине стержня [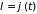 ]
уравнение
]
уравнение
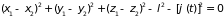
содержат время, и связь является нестационарной.
Так как каждый
вектор
имеет три проекции, то положение системы
заданной конфигурации определяется
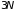 –координатами.
Для свободной системы (отсутствуют
внутренние связи) все
координат являются независимыми. При
наличии связей независимы только
–координатами.
Для свободной системы (отсутствуют
внутренние связи) все
координат являются независимыми. При
наличии связей независимы только
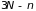 координат. Число независимых параметров,
определяющих положение механической
системы в пространстве, называют числом
степеней свободы системы.
координат. Число независимых параметров,
определяющих положение механической
системы в пространстве, называют числом
степеней свободы системы.
Уравнения (1.8)
позволяют исключить
координат из общего числа
и ввести независимые переменные
обобщенные координаты
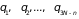 ,
через которые и выражаются координаты
:
,
через которые и выражаются координаты
:
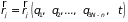 ,
,
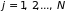 .
.
Обобщенными
координатами называют параметры,
определяющие положение механической
системы в пространстве. Их число равно
числу степеней свободы или больше.
Обобщенные скорости определяются как
производные от обобщенных координат
по времени
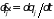 .
Кинетическая энергия
свободной системы и системы со
стационарными связями является
квадратичной формой обобщенных скоростей
и не зависит от времени
.
Кинетическая энергия
свободной системы и системы со
стационарными связями является
квадратичной формой обобщенных скоростей
и не зависит от времени
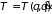 ,
,
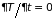 .
Здесь
.
Здесь
 и
и
 – совокупность обобщенных координат
и скоростей.
– совокупность обобщенных координат
и скоростей.
Каждой обобщенной
координате
 соответствует своя обобщенная сила
соответствует своя обобщенная сила
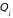 ,
определяющая элементарную работу в
системе с
,
определяющая элементарную работу в
системе с
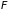 степенями свободы.
степенями свободы.
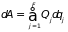 .
.
В отсутствие
зависимости от обобщенных скоростей,
т.е.
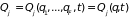 (
( ),
то существует такая функция
),
то существует такая функция
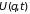 ,
что
,
что
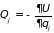 . (1.9)
. (1.9)
Силы
называют потенциальными, а функцию
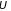 – потенциальной энергией (определена
с точностью до произвольной постоянной).
Работа потенциальных сил равна убыли
потенциальной энергии
– потенциальной энергией (определена
с точностью до произвольной постоянной).
Работа потенциальных сил равна убыли
потенциальной энергии
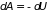 .
К непотенциальным силам относятся силы
трения. Они направлены против смещения,
так что
.
К непотенциальным силам относятся силы
трения. Они направлены против смещения,
так что
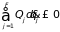 .
Эти силы называют диссипативными: здесь
происходит превращение механической
энергии в тепловую.
.
Эти силы называют диссипативными: здесь
происходит превращение механической
энергии в тепловую.
В основу молекулярной
теории макроскопических систем положена
модель вещества как механической
системы, где частицы движутся в пустоте,
а силы их взаимодействия потенциальны.
Поэтому, в дальнейшем рассматриваются
только системы, в которых все силы
являются потенциальными. При внешних
воздействиях потенциал
зависит не только от координат точечных
масс системы, но также от внешних
параметров, к которым относятся, в
частности, координаты стенок сосуда,
где находится система; зарядов (источники
электрического поля); магнитов (источники
магнитного поля), тел большой массы,
создающих гравитационное поле, и т.д. В
качестве внешних параметров при наличии
внешнего электрического или магнитного
поля задают их напряженности. Для
свободной системы или системы со
стационарными связями в постоянном
внешнем поле потенциальная энергия не
зависит от времени
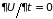 ,
т.е.
,
т.е.
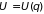 .
Когда все связи (если они имеются)
стационарны, внешние и внутренние силы
потенциальны, потенциальная энергия
явно не зависит от времени, система
называется консервативной. В частности,
к консервативной системе относится
замкнутая (изолированная) система, в
отсутствие внешних полей. Для систем,
все силы в которых потенциальны, вводится
понятие обобщенный импульс
.
Когда все связи (если они имеются)
стационарны, внешние и внутренние силы
потенциальны, потенциальная энергия
явно не зависит от времени, система
называется консервативной. В частности,
к консервативной системе относится
замкнутая (изолированная) система, в
отсутствие внешних полей. Для систем,
все силы в которых потенциальны, вводится
понятие обобщенный импульс
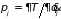 (
).
Совокупность переменных
,
,
называют каноническими
переменными,
или переменными Гамильтона. Именно
они используются в статистических
распределениях.
(
).
Совокупность переменных
,
,
называют каноническими
переменными,
или переменными Гамильтона. Именно
они используются в статистических
распределениях.
В механике для описания движения системы со стационарными связями и потенциальными силами, вводят функцию Гамильтона
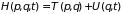 . (1.10)
. (1.10)
Она определяет полную энергию системы, выраженную через канонические переменные. Из принципа наименьшего действия следуют канонические уравнения движения (уравнения Гамильтона)
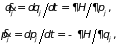 (1.11)
(1.11)
– дифференциальные
уравнения первого порядка; их число
равно
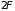 –удвоенному числу степеней свободы.
Их решение
–удвоенному числу степеней свободы.
Их решение
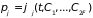 ;
;
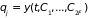 ,
,
справедливое для
любого движения при заданной функции
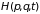 ,
зависит от
постоянных интегрирования
,
зависит от
постоянных интегрирования
 .
Последние находятся из начальных
условий:
значений
.
Последние находятся из начальных
условий:
значений
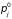 и
и
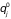 (
)
при
(
)
при
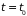 .
Они определяют все последующие состояния
системы и единственное решение уравнений
(1.11).
.
Они определяют все последующие состояния
системы и единственное решение уравнений
(1.11).
Поскольку в общем случае обобщенные координаты и импульсы зависят от времени, то изменение функции Гамильтона при движении системы происходит в соответствии с соотношениями
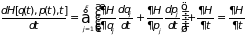 . (1.12)
. (1.12)
Здесь учтены
уравнения движения (1.11), которые приводят
к равенству нулю выражения в скобках
при любом
.
Для консервативной системы
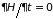 и
и
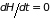 ,
следовательно, ее энергия при движении
системы остается постоянной.
,
следовательно, ее энергия при движении
системы остается постоянной.
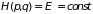 .
.
Функция
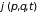 есть интеграл движения, если она
является постоянной величиной, т.е.
есть интеграл движения, если она
является постоянной величиной, т.е.
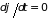 ,
или в развернутом виде
,
или в развернутом виде
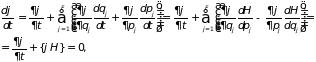 (1.13)
(1.13)
где
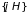 – скобки Пуассона. Это равенство-необходимое
и достаточное условие того, что функция
есть интеграл движения. В отсутствие
зависимости от времени функция
– скобки Пуассона. Это равенство-необходимое
и достаточное условие того, что функция
есть интеграл движения. В отсутствие
зависимости от времени функция
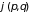 будет интегралом движения, если
будет интегралом движения, если
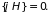 (1.14)
(1.14)
1.2.2. Фазовое
пространство – многомерное эвклидово
пространство, координатами которого
являются
обобщенных координат
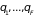 и импульсов
и импульсов
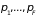 .
Его число измерений равно удвоенному
числу
степеней свободы системы. Заданному
механическому состоянию системы (
.
Его число измерений равно удвоенному
числу
степеней свободы системы. Заданному
механическому состоянию системы (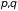 )
в фазовом пространстве отвечает
изобразительная точка. Различают
-пространство
– фазовое пространство одной частицы
и
)
в фазовом пространстве отвечает
изобразительная точка. Различают
-пространство
– фазовое пространство одной частицы
и
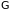 -пространство
– фазовое пространство системы
(совокупности частиц).
-пространство
– фазовое пространство системы
(совокупности частиц).
Число измерений
-пространства
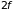 ,
для одноатомной системы оно шестимерное,
осями его являются
,
для одноатомной системы оно шестимерное,
осями его являются
 .
-пространство
имеет
измерений. Для системы из
атомов фазовое пространство
-мерное
(
осей
и
осей
.
-пространство
имеет
измерений. Для системы из
атомов фазовое пространство
-мерное
(
осей
и
осей
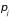 ).
Состояние всех
частиц изобразится одной точкой в
-пространстве,
но тоже состояние всех
частиц можно изобразить совокупностью
точек в
-пространстве.
-пространство
является подпространством
-пространства.
).
Состояние всех
частиц изобразится одной точкой в
-пространстве,
но тоже состояние всех
частиц можно изобразить совокупностью
точек в
-пространстве.
-пространство
является подпространством
-пространства.
Эволюцию во времени
изобразительной точки описывает фазовая
траектория – непрерывная кривая,
которая проходит через точку
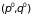 ,
отвечающую начальному состоянию системы.
Фазовая траектория консервативной
системы лежит на гиперповерхности,
определяемой уравнением
,
отвечающую начальному состоянию системы.
Фазовая траектория консервативной
системы лежит на гиперповерхности,
определяемой уравнением
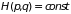 .
В силу единственности решения уравнения
(1.11) фазовая траектория не может иметь
точек пересечения сама с собой (но может
иметь характер замкнутой кривой).
.
В силу единственности решения уравнения
(1.11) фазовая траектория не может иметь
точек пересечения сама с собой (но может
иметь характер замкнутой кривой).
В дальнейшем
состояние системы будем определять,
задавая некоторый бесконечно малый
интервал, в котором находятся значения
и
,
а именно: интервал от
до
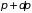 и от
до
и от
до
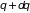 .
Элемент объема в фазовом
-пространстве
есть
.
Элемент объема в фазовом
-пространстве
есть
 , (1.15)
, (1.15)
где
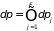 ,
,
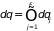 –- элементы объема в импульсном и
координатном пространствах. Элемент
объема в
-пространстве
–- элементы объема в импульсном и
координатном пространствах. Элемент
объема в
-пространстве
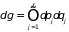 . (1.16)
. (1.16)
Очевидно, что
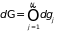 , (1.17)
, (1.17)
где
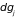 – элемент объема в фазовом пространстве
-ой
частицы. В качестве примера определим
элемент фазового объема системы свободных
(не взаимодействующих друг с другом)
частиц, движущихся в некотором объеме
,
в отсутствие внешних полей. Каждая из
них имеет три степени свободы
– элемент объема в фазовом пространстве
-ой
частицы. В качестве примера определим
элемент фазового объема системы свободных
(не взаимодействующих друг с другом)
частиц, движущихся в некотором объеме
,
в отсутствие внешних полей. Каждая из
них имеет три степени свободы
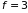 .
Энергия такой системы есть кинетическая
энергия поступательного движения
частиц. Координаты каждой из них могут
принимать любые значения в пределах
объема
,
а энергия – равна
.
Энергия такой системы есть кинетическая
энергия поступательного движения
частиц. Координаты каждой из них могут
принимать любые значения в пределах
объема
,
а энергия – равна
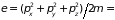
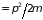 .
Элемент объема в
-пространстве,
отвечающий состояниям с энергией частицы
в интервале от
.
Элемент объема в
-пространстве,
отвечающий состояниям с энергией частицы
в интервале от
 до
до
 равен
равен
 .
.
Так как всем
состояниям (разным значениям проекции
импульса) с заданным значением импульса
отвечает одинаковая энергия, то в
пространстве импульсов изобразительные
точки лежат на сфере радиуса
 .
Состояниям с энергией в интервале от
до
соответствует сферический слой между
радиусами
и
,
объем которого равен
.
Состояниям с энергией в интервале от
до
соответствует сферический слой между
радиусами
и
,
объем которого равен
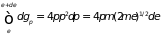 .
.
Отсюда следует объем энергетического слоя (элементарный объем) в -пространстве как функция энергии частицы :
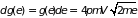 . (1.18)
. (1.18)
Величина
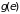 –объем фазового пространства вблизи
энергии
,
отнесенный к единичному интервалу
изменения энергии; она называется
энергетической плотностью состояния.
Фазовый объем
–объем фазового пространства вблизи
энергии
,
отнесенный к единичному интервалу
изменения энергии; она называется
энергетической плотностью состояния.
Фазовый объем
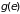 ,
в котором отвечает точками частиц с
энергией, равной или меньшей заданной
(
,
в котором отвечает точками частиц с
энергией, равной или меньшей заданной
(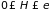 ),
находится интегрированием (1.18):
),
находится интегрированием (1.18):
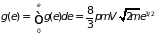 . (1.19)
. (1.19)
Соответствующие
ему объемы в подпространстве импульсов
(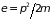 )
и фазовом пространстве определяется
выражениями
)
и фазовом пространстве определяется
выражениями
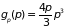 ,
,
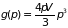 (1.20)
(1.20)
В -мерном -пространство элемент объема системы из свободных частиц (идеальный газ), и его элемент объема
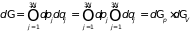 , (1.21)
, (1.21)
где
 ,
,
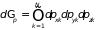 . (1.22)
. (1.22)
Если система ограничена объемом , то
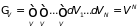 . (1.23)
. (1.23)
а её кинетическая энергия
 (1.24)
(1.24)
Фазовый объем системы с фиксированными и , в котором находятся точечные массы с энергией, равной или меньшей , равен
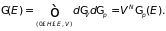 (1.25)
(1.25)
Здесь
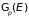 – результат интегрирования по импульсам
при условии
– результат интегрирования по импульсам
при условии
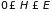 и представляет объем
-мерной
сферы в пространстве импульсов радиуса
и представляет объем
-мерной
сферы в пространстве импульсов радиуса
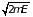 .
.
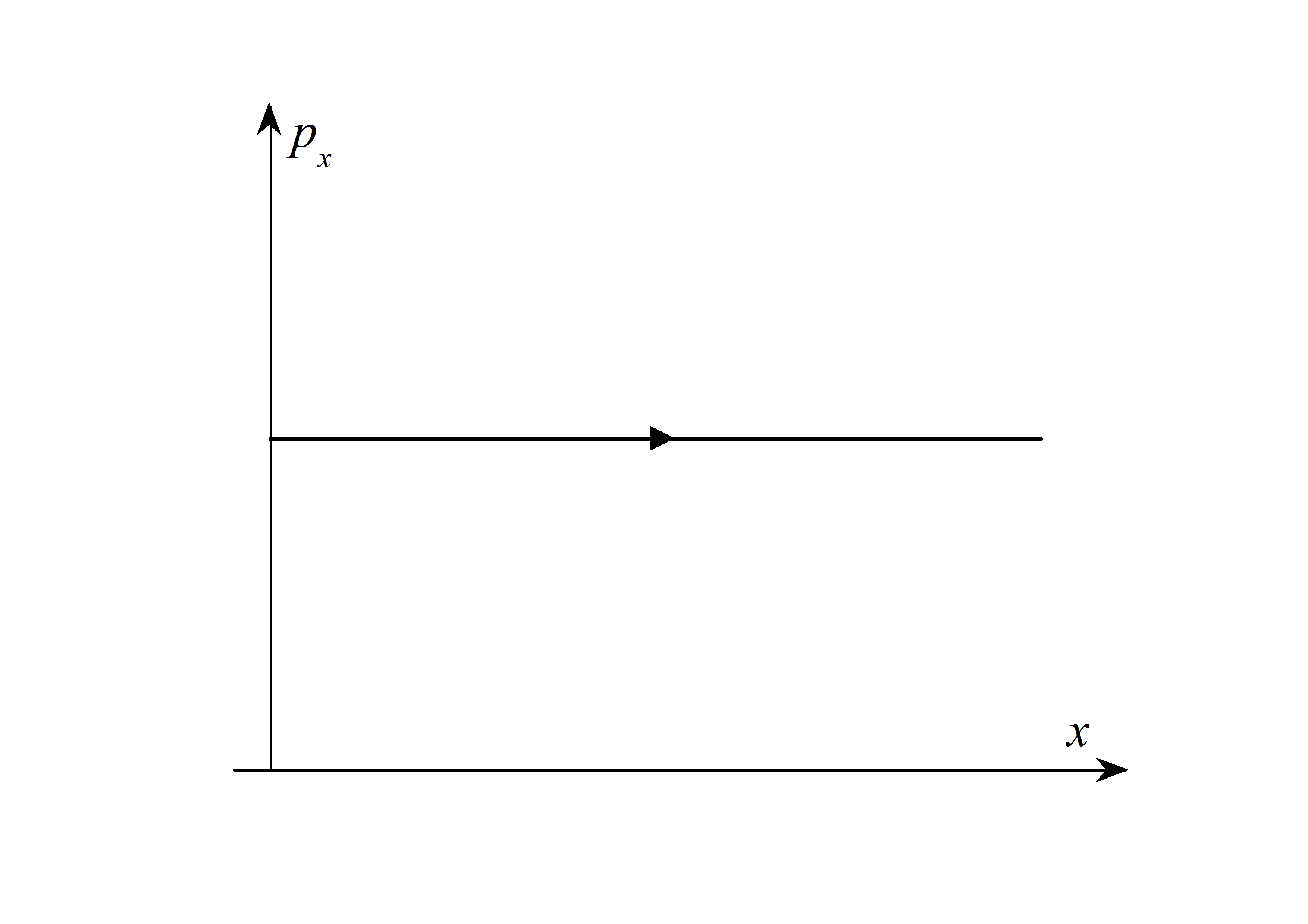
Наглядно представить
фазовую траекторию можно только в
двумерном пространстве. Речь идет о
системах с одной степенью свободы,
например, о частице движущейся равномерно
вдоль оси
 (рис. 1.1), или про одномерный гармонический
осциллятор. Одномерным гармоническим
осциллятором называют точечную массу,
совершающую колебательное движение в
одном измерении, если действующая на
нее сила
(рис. 1.1), или про одномерный гармонический
осциллятор. Одномерным гармоническим
осциллятором называют точечную массу,
совершающую колебательное движение в
одном измерении, если действующая на
нее сила
 пропорциональна смещению
от положения равновесия
пропорциональна смещению
от положения равновесия
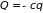 (
( – силовая постоянная). Зависимость
потенциальной энергии
от смещения
– силовая постоянная). Зависимость
потенциальной энергии
от смещения
|
найдем,
проинтегрировав соотношение
Кинетическая энергия и обобщенный импульс есть |
Рис. 1.1. |
Функция Гамильтона линейного осциллятора (1.10) запишется как
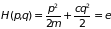 . (1.26)
. (1.26)
Заданному
колебательному движению отвечает
энергия
 ,
а его уравнение (1.11) принимает вид
,
а его уравнение (1.11) принимает вид
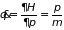 ;
;
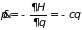 . (1.27)
. (1.27)
Исключив
и введя циклическую частоту
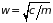 ,
приходим к уравнению колебаний
,
приходим к уравнению колебаний
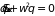 , (1.28)
, (1.28)
решением которого является функция
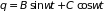 . (1.29)
. (1.29)
С учетом начальных
условий
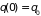 ,
,
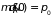 при
при
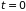 имеем
имеем
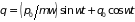 или
или
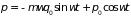 . (1.30)
. (1.30)
Это решение можно представить по-иному
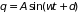 или
или
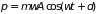 , (1.31)
, (1.31)
где амплитуда
и начальная фаза
 колебаний равны
колебаний равны
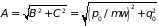 ,
,
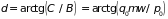 .
.
Подстановка (1.31)
в (1.26) дает
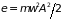 ,
а из (1.31) следует уравнение фазовой
траектории
,
а из (1.31) следует уравнение фазовой
траектории
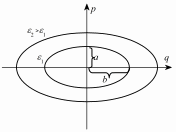
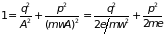 (1.32)
(1.32)
|
– уравнение
эллипса с полуосями
(1.33) |
Рис. 1.2. |
Большей энергии осциллятора отвечает эллипс с большими полуосями.

 (1.9). Если принять, что в равновесии при
(1.9). Если принять, что в равновесии при
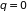
 ,
то
,
то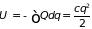 .
.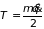 ;
;
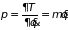 .
.
 и
и
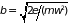 (рис. 1.2). Площадь эллипса
определяется энергией осциллятора и
его частотой
(рис. 1.2). Площадь эллипса
определяется энергией осциллятора и
его частотой
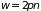 :
: