5.3. Флуктуации термодинамических величин в однородной среде
5.3.1. Базовые соотношения. Критерии устойчивости равновесия. Рассматриваются флуктуации термодинамических величин системы, погруженной в термостат. Считая переход системы из начального (равновесного) в конечное, флуктуационное состояние обратимым, воспользуемся выражением для минимальной работы (см. раздел «Работа тепловых машин однократного действия»):
,
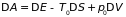где
,
,
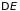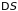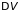– изменения энергии, энтропии и объема
системы при флуктуации, а
и
– температура и давление термостата,
т.е. равновесное (среднее) значение
температуры и давления системы. После
подстановки
в (5.4) имеем
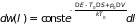. (5.6)
В таком виде формула
применима к любым флуктуациям – как
малым, так и большим. Под последними
понимаются такие, при которых, например,
сравнимо с энергией самой малой части
системы, но, конечно, по-прежнему мало
по сравнению с энергией системы в целом.
Для малых флуктуаций, представляя
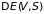рядом до членов второго порядка малости,
получим
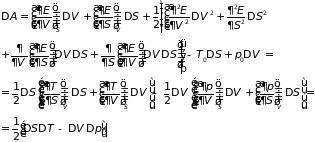
При
вычислении
использованы значения обобщенных сил
системы
,
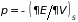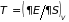в равновесном состоянии (
и
).
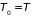Таким образом. Вероятность флуктуаций
различных термодинамических параметров
определяется формулой
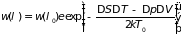(5.7)
Устойчивым является
такое состояние системы, когда она
находится в равновесии с окружающей
средой. При этом его вероятность
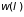имеет максимум, когда
,
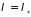где
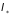– наиболее вероятное значение (для
макросистем
).
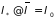Поэтому при любых отклонениях от
равновесия обязано выполняться
неравенство
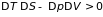. (5.8)
При постоянном
значении одного из параметров в первом
слагаемом (
или
),
либо – во втором (
или
),
имеют место неравенства
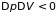и
.
Следствием их есть частные условия
(критерии) устойчивости равновесия (см.
разд. 6)
;
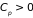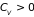; (5.9)
;
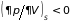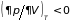. (5.10)
При отрицательных теплоемкостях тело можно было бы нагревать, забирая при этом от него тепло, т.е. построить вечный двигатель второго рода.
Полученные условия
термической (
,
)
и механической (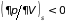
,
)
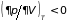устойчивости являются достаточными
для устойчивости состояния однородной
системы. Эти условия не обязательно
выполняются в неоднородной среде,
например, в системе, находящейся в поле
внешних сил или состоящей из нескольких
фаз. В этом случае состояние системы
помимо параметров
,
,
и
зависит от других величин, в частности,
концентрации, напряженностей внешних
полей и других факторов. С учетом
последних меняется выражение для работы.
5.3.2. Флуктуации объема и температуры. Считая независимыми переменные и , имеем
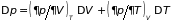, (5.11.а)
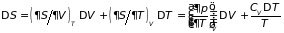. (5.11.б)
Подставляя эти
выражения в показатель формулы (5.7),
найдем, что члены с
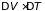сокращаются
и остается
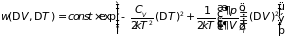(5.12)
Видно, что искомая
вероятность распадается на два независимых
множителя, зависящие только от
и
(
).
Другими словами, флуктуации температуры
и объема статистически независимы, а
поэтому
.
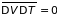Сравнивая каждый
из двух сомножителе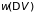й
и
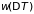с общей формулой распределения Гаусса,
найдем следующие выражения для дисперсии
температуры и объема:
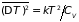; (5.13.а)
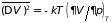. (5.13.б)
Считаем
внутреннюю энергию функцией объема и
температуры. С учетом основного
термодинамического равенства и связи
ее отклонение можно выразить следующим
образом
.
Возведя в квадрат и усредняя, получим
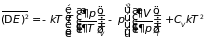. (5.14)
Здесь использованы формулы (5.13) и независимость флуктуации температуры и объема.
5.3.3. Флуктуации давления и энтропии. Если в качестве независимых переменных выбрать и , то
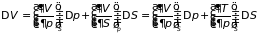; (5.15а)
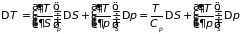. (5.15б)
Подставляя эти выражения в (5.), находим
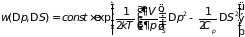. (5.16)
Как и в предыдущем
случае,
,
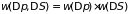откуда следует
,
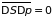что отвечает условию независимости флуктуаций энтропии и давления
Средние квадраты флуктуаций оказываются равными
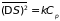, (5.17)
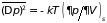. (5.18)
Положительность
дисперсии флуктуаций энтропии
обеспечивается неравенством
,
.
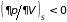5.3.4.
Флуктуации
числа частиц и плотности.
Радиус
корреляции.
Формула (5.13б) определяет дисперсию
объема системы, содержащей определенное
число
частиц. Деля обе стороны равенства на
,
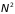находим дисперсию объема, приходящегося
на одну частицу:
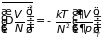. (5.19)
Она не зависит от
того, рассматривается флуктуация в
постоянном объеме или при постоянном
числе частиц. Поэтому из (5.19) вычисляется
флуктуация числа частиц в заданном
объеме (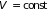
).
Учитывая, что
,
имеем
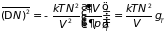, (5.20а)
где
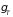– изотермическая сжимаемость.
В некоторых
вычислениях удобно представить дисперсию
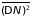в ином виде. Среднее число частиц в
системе, имеющей диффузный контакт с
термостатом (при постоянных объеме и
температуре), определяется формулой
,
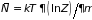где функция состояния имеет вид
.
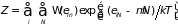Вычисления дают
.
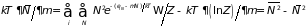что позволяет выразить дисперсию числа частиц следующим образом
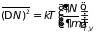. (5.20б)
Для идеального
газа (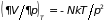
)
из (5.20а) имеем
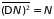. (5.21)
Независимость флуктуации числа частиц идеального газа в данном объеме от температуры связаны с тем, что движение каждой частицы происходит независимо от движения остальных. С ростом температуры в идеальном газе увеличивается лишь средняя квадратичная скорость, но сам характер движения не изменяется.
Поскольку плотность
вещества равна
,
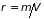где
– масса, заключенная в объеме
,
то вычисление дисперсии ее флуктуации
дает
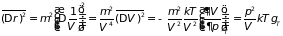. (5.22)
Формулы,
включающие изотермическую сжимаемость
(
),
например, (5.12) и (5.13б), теряют смысл, когда
(а
).
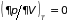В этом случае изменяется выражение для
работы
,
ее разложение в ряд должно быть продолжено
до величин более высокого порядка
малости.
Если
флуктуации каких-либо параметров
,
взаимно зависимые, то
,
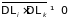а степень этой зависимости отражает
коэффициент
(радиус)
корреляции
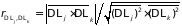. (5.23)
Такими зависимыми могут быть флуктуации объема и давления при произвольных значениях температуры и объема. Учитывая (5.11а), имеем:
. .
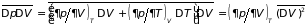Здесь учтено, что
.
Воспользовавшись (5.13б) и (5.18), найдем
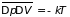и определим радиус корреляции
.
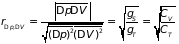