
- •1. Основные положения статистической термодинамики
- •1.1. Понятия и начала феноменологической термодинамики.
- •1.2. Микроскопическое (механическое) описание классических систем.
- •1.3. Особенности представления квантовых систем
- •1.4. Вероятность нахождения системы в элементе фазового пространства. Метод ансамблей Гиббса.
- •1.5. Макроскопические величины как фазовые средние
- •1.6. Распределение в системах с постоянным числом частиц
- •1.6.2. Распределения Гиббса.
- •1.6.3. Квазиклассическое приближение.
- •1.7. Свойства распределения Гиббса
- •1.8. Большое каноническое распределение Гиббса
- •2. Статистика идеального газа
- •2.1. Идеальный газ как модель статистической системы
- •2.2. Распределение Максвелла
- •2.3. Столкновения молекул со стенкой сосуда. Давление
- •2.4. Характерные величины идеального газа
- •2.5. Столкновение молекул между собой
- •2.6. Длина свободного пробега
- •2.7. Идеальный газ во внешнем поле
- •2.8. Число и функция состояний идеального газа
- •2.9. Классическая теория теплоемкости газа двухатомных молекул
- •2.10. Квантовая теория теплоемкости газа двухатомных молекул
- •2.11. Распределения в квантовых системах
- •3. Законы термодинамики
- •3.1. Статистическое обоснование первого начала термодинамики
- •3.2. Второе начало термодинамики
- •3.3. Вечный двигатель второго рода. Максимальная работа процессов
- •3.4. Полезная работа тепловых машин
- •3.5. Метод термодинамических потенциалов
- •3.6. Термодинамические коэффициенты. Критерии устойчивости равновесия
- •3.7. Статистическое вычисление термодинамических величин
- •3.8. Третье начало термодинамики (теорема Нернста)
- •3.9. Применения термодинамики
- •4. Статистика сложных систем.
- •4.1. Модель кристаллического твердого тела. Уравнение движения атомов
- •4.2. Дисперсионное уравнение нормальных колебаний кристалла
- •4.3. Кристалл как система линейных гармонических осцилляторов
- •4.4. Статистическая сумма и энергия кристалла (в гармоническом приближении)
- •4.5. Теория теплоемкости Дебая
- •4.6. Электронный газ в металлах
- •4.7. Зависимость энергии электрона от волнового вектора. Эффективная масса
- •4.8. Теория парамагнетизма. Природа и характеристики магнетизма.
- •4.9. Равновесное излучение.
- •4.10. Системы с кулоновским взаимодействием частиц.
- •5. Теория малых флуктуаций
- •5.1. Определение и значение флуктуаций
- •5.2. Мера вероятности и масштаб флуктуаций
- •5.3. Флуктуации термодинамических величин в однородной среде
- •5.4. Предельная чувствительность измерительных приборов
- •5.5. Рассеяния света флуктуациями
- •6. Элементы теории физической кинетики
- •6.1. Определения и характеристики необратимых процессов
- •6.2. Теория стационарных процессов в газе свободных электронов
- •6.3. Газокинетическое уравнение Больцмана
- •6.4. Приближение времени релаксации
- •Раздел 2
- •Раздел 2
- •Раздел 3
- •Раздел 4
- •Раздел 5
- •Раздел 6
- •Список Литературы
1.6.2. Распределения Гиббса.
Чтобы определить
явный вид функции распределения, следует
вычислить вероятность
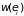 найти систему в состоянии с энергией
между
и
найти систему в состоянии с энергией
между
и
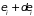 (
(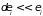 ,
индекс
,
индекс
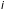 пробегает ряд значений). Каждому значению
энергии
в квазиклассическом приближении отвечает
некоторая группа состояний. Рассмотрим
замкнутую систему, которая не
взаимодействует с окружающими телами
(термостатом). Здесь под замкнутой
условно понимается система, энергия
которой за все время наблюдения остается
заключенной в заданных весьма узких
пределах
пробегает ряд значений). Каждому значению
энергии
в квазиклассическом приближении отвечает
некоторая группа состояний. Рассмотрим
замкнутую систему, которая не
взаимодействует с окружающими телами
(термостатом). Здесь под замкнутой
условно понимается система, энергия
которой за все время наблюдения остается
заключенной в заданных весьма узких
пределах
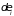 (абсолютно замкнутых систем в природе
не существует!). Поскольку все состояния
с данной энергией и числом частиц
равноправны и равновероятны, то
вероятность того, что замкнутая система
находится в одном из них, будет просто
пропорциональная числу состояний с
данной энергией (кратности его вырождения)
(абсолютно замкнутых систем в природе
не существует!). Поскольку все состояния
с данной энергией и числом частиц
равноправны и равновероятны, то
вероятность того, что замкнутая система
находится в одном из них, будет просто
пропорциональная числу состояний с
данной энергией (кратности его вырождения)
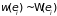 . (1.48)
. (1.48)
Формула получила
название микроканоническое распределение
Гиббса. Здесь имеет место определенная
аналогия с классическим представлением
формулы (1.42): чем больше выбран элементарный
объем фазового пространства
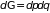 ,
тем больше вероятность застать в нем
изобразительную точку. Микроканоническое
распределение является принципиальной
основой статистической физики.
,
тем больше вероятность застать в нем
изобразительную точку. Микроканоническое
распределение является принципиальной
основой статистической физики.
На практике значительно чаще приходится иметь дело с макроскопическими системами, слабо взаимодействующими с термостатом. Мысленно объединим исследуемую подсистему и термостат в одну общую замкнутую систему. Ее суммарная энергия (термостата и подсистемы) почти постоянная величина
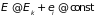 . (1.49)
. (1.49)
Здесь
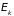 – энергия термостата, находящегося в
-ом
состоянии,
–
энергия подсистемы в
-ом
состоянии. Знак
(«почти») означает, что формула не
учитывает взаимодействия сложной
системы с остальными окружением и
взаимодействие между термостатом и
подсистемой. Подсистема может находится
в любом состоянии с энергией
,
а термостат – в любом состоянии с
энергией
.
Изменение состояния подсистемы не
влияет на состояние термостата и
наоборот, если указанные переходы не
выводят систему из группы состояний с
энергией
,
а термостат, соответственно, из состояний
с энергией
.
– энергия термостата, находящегося в
-ом
состоянии,
–
энергия подсистемы в
-ом
состоянии. Знак
(«почти») означает, что формула не
учитывает взаимодействия сложной
системы с остальными окружением и
взаимодействие между термостатом и
подсистемой. Подсистема может находится
в любом состоянии с энергией
,
а термостат – в любом состоянии с
энергией
.
Изменение состояния подсистемы не
влияет на состояние термостата и
наоборот, если указанные переходы не
выводят систему из группы состояний с
энергией
,
а термостат, соответственно, из состояний
с энергией
.
Вероятность
реализации состояния сложной замкнутой
системы (термостат и подсистема) с
фиксированной энергией (1.49) определяется
микроканоническим распределением
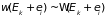 .
С другой стороны, число состояний сложной
системы из двух независимых частей
равно
.
С другой стороны, число состояний сложной
системы из двух независимых частей
равно
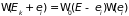 . (1.50)
. (1.50)
Вероятность
нахождения системы в состоянии с энергией
(а термостат в состоянии с энергией
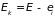 )
пропорциональна
)
пропорциональна
 . (1.51)
. (1.51)
При больших размерах
термостата его энергия значительно
превышает энергию подсистемы
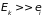 ,
,
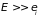 .
Поэтому любые изменения энергии
подсистемы практически не влияют на
энергию термостата; все состояния
термостата (при изменении состояний
подсистемы) можно считать принадлежащими
к одной и той же энергии.
.
Поэтому любые изменения энергии
подсистемы практически не влияют на
энергию термостата; все состояния
термостата (при изменении состояний
подсистемы) можно считать принадлежащими
к одной и той же энергии.
С учетом указанных
замечаний можно разложить функцию
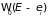 в ряд по степеням малой величины
и ограничится линейными слагаемыми.
Однако, разлагать в ряд непосредственно
саму функцию
нельзя, потому что число состояний –
мультипликативная, а энергия – аддитивная
функции. Представления в виде ряда
в ряд по степеням малой величины
и ограничится линейными слагаемыми.
Однако, разлагать в ряд непосредственно
саму функцию
нельзя, потому что число состояний –
мультипликативная, а энергия – аддитивная
функции. Представления в виде ряда
 (1.52)
(1.52)
не
обладает требуемыми свойствами. Так,
для двух систем с числом состояний
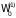 и
и
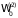 и энергиями
и энергиями
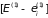 и
и
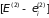 общая энергия должна быть суммой
общая энергия должна быть суммой
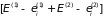 ,
а общее число состояний должно равняться
,
а общее число состояний должно равняться
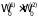 .
Но при перемножении левых частей
разложения (1.52) правые части не
складываются. Поэтому представим число
состояний в виде
.
Но при перемножении левых частей
разложения (1.52) правые части не
складываются. Поэтому представим число
состояний в виде
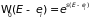 , (1.53)
, (1.53)
где
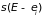 – новая функция аргумента
– новая функция аргумента
 .
Как будет показано в дальнейшем, она
имеет смысл статистической энтропии.
Представление (1.53) оправдано, поскольку
по своей природе число состояний –
существенно положительная величина,
значение которой заведомо не меньше
единицы. Кроме того, поскольку
.
Как будет показано в дальнейшем, она
имеет смысл статистической энтропии.
Представление (1.53) оправдано, поскольку
по своей природе число состояний –
существенно положительная величина,
значение которой заведомо не меньше
единицы. Кроме того, поскольку
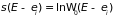 ,
то
,
подобно энергии, является аддитивной
функцией.
,
то
,
подобно энергии, является аддитивной
функцией.
Разлагая в ряд, ограничиваясь линейным членом, имеем
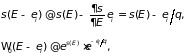 (1.54)
(1.54)
где величина
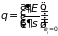 (1.55)
(1.55)
получила название
модуля распределения (статистической
температуры). В следующем разделе
будет показано, что статистическая
температура связана с абсолютной
температурой простым соотношением
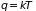 ,
где
– постоянная Больцмана. Нетрудно видеть,
что (1.54) удовлетворяет требованиям
мультипликативности
,
где
– постоянная Больцмана. Нетрудно видеть,
что (1.54) удовлетворяет требованиям
мультипликативности
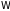 при сложении энергий независимых частей:
при сложении энергий независимых частей:
 .
Подставляя (1.54) в (1.51) дает
.
Подставляя (1.54) в (1.51) дает
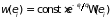 . (1.56)
. (1.56)
Здесь через
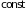 обозначены параметры, не зависящие от
значения
и свойств подсистемы. Формула определяет
вероятность того, что слабо взаимодействующая
часть некоторого собрания произвольных
физических систем будет находиться в
одном из
обозначены параметры, не зависящие от
значения
и свойств подсистемы. Формула определяет
вероятность того, что слабо взаимодействующая
часть некоторого собрания произвольных
физических систем будет находиться в
одном из
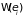 состояний с энергией между
и
,
а термостат – в одном из состояний с
энергией между
состояний с энергией между
и
,
а термостат – в одном из состояний с
энергией между
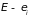 и
и
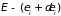 .
Но так как состояние термостата не
представляет интереса, для краткости
говорят, что
– вероятность нахождения подсистемы
в одном из состояний с энергией
.
Из определения вероятности следует
условие нормировки
.
Но так как состояние термостата не
представляет интереса, для краткости
говорят, что
– вероятность нахождения подсистемы
в одном из состояний с энергией
.
Из определения вероятности следует
условие нормировки
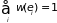 , (1.57а)
, (1.57а)
где суммирование
ведется по всем возможным квантовым
состояниям системы. Отсюда вытекает,
что введенный формально коэффициент
 является существенно положительной
величиной:
является существенно положительной
величиной:
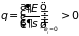 . (1.57б)
. (1.57б)
Только в этом случае вероятность состояний сколь угодно больших энергий стремится к нулю. Постоянная в (1.56) находится из условия нормировки
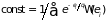 ,
,
и распределение вероятностей принимает вид
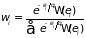 . (1.58)
. (1.58)
Оно впервые предложено Дж. Гиббсом (1901 г) для классических систем и получило название распределение Гиббса или канонического распределения. Сумма, стоящая в знаменателе, играет большую роль в статистической физике, для нее введено специальное обозначение
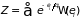 , (1.59)
, (1.59)
и принято называть
функцией (интегралом) состояния
(статистической суммой). Распределение
Гиббса позволяет вычислить среднее
значение любой физической величины
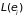 ,
зависящей от состояния системы:
,
зависящей от состояния системы:
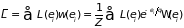 . (1.60)
. (1.60)
