4.6. Электронный газ в металлах

4.6.1. Модель свободных электронов. Металлы – тела, которые, кроме характерного блеска и пластичности, обладают высокой тепло- и электропроводностью. Это заставляет предположить, что металлы содержат большое число высокоподвижных электронов, которые не связаны ни с какими атомами, свободно перемещаются по всему кристаллу. На языке квантовой теории можно говорить о том, что волновая функция данного электрона «размазана» в пространстве, а не локализована вблизи какого-то атома. Одно из наиболее успешных приближений в теории металлов – модель свободных электронов. Предполагается, что металл состоит из решетки ионных остовов (структурных единиц), каждый из которых имеет ядро с оболочкой из сильно связанных электронов и большого числа практически независимых электронов. Последние обычно считают полностью свободными, а металл – «ящиком», содержащим их. Совокупность свободных электронов называют электронным газом. Теория кристаллов, построенная на указанной модели, хорошо объясняет их электрические и магнитные свойства, термомагнитные, гальваномагнитные явления (эффект Холла, термоэлектронную эмиссию и др.).

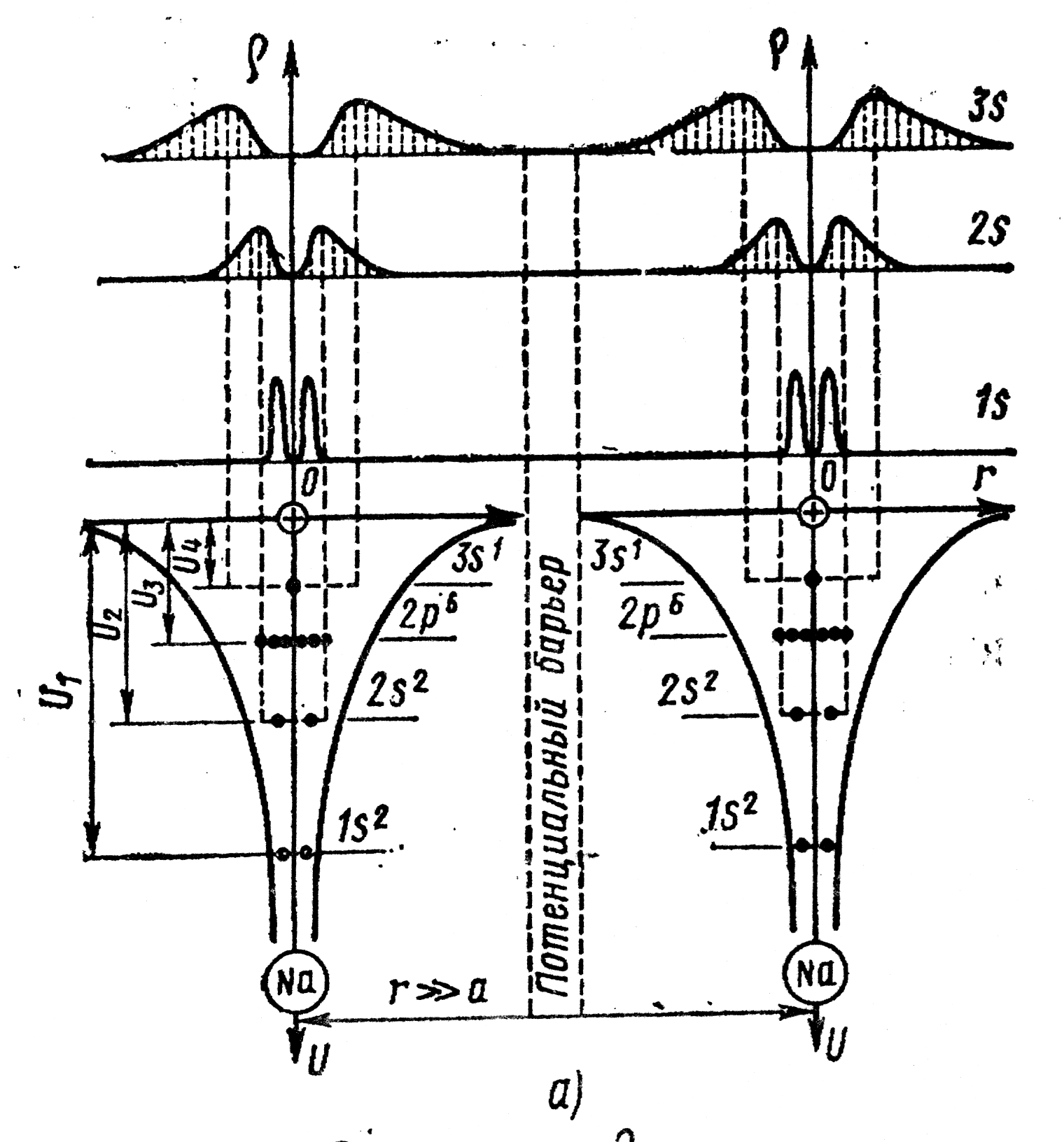
4.6.2. Обобществление электронов легко понять на следующем идеализированном примере. Рассмотрим два изолированных атома натрия ( ), у которого уровни энергии 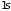, , 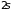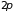полностью укомплектованы электронами, а уровень 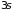укомплектован наполовину. (Рис. 4.5, а) Атомы отделены друг от друга потенциальным барьером толщиной 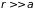. Высота барьеров для электронов, находящихся на различных уровнях, различна. 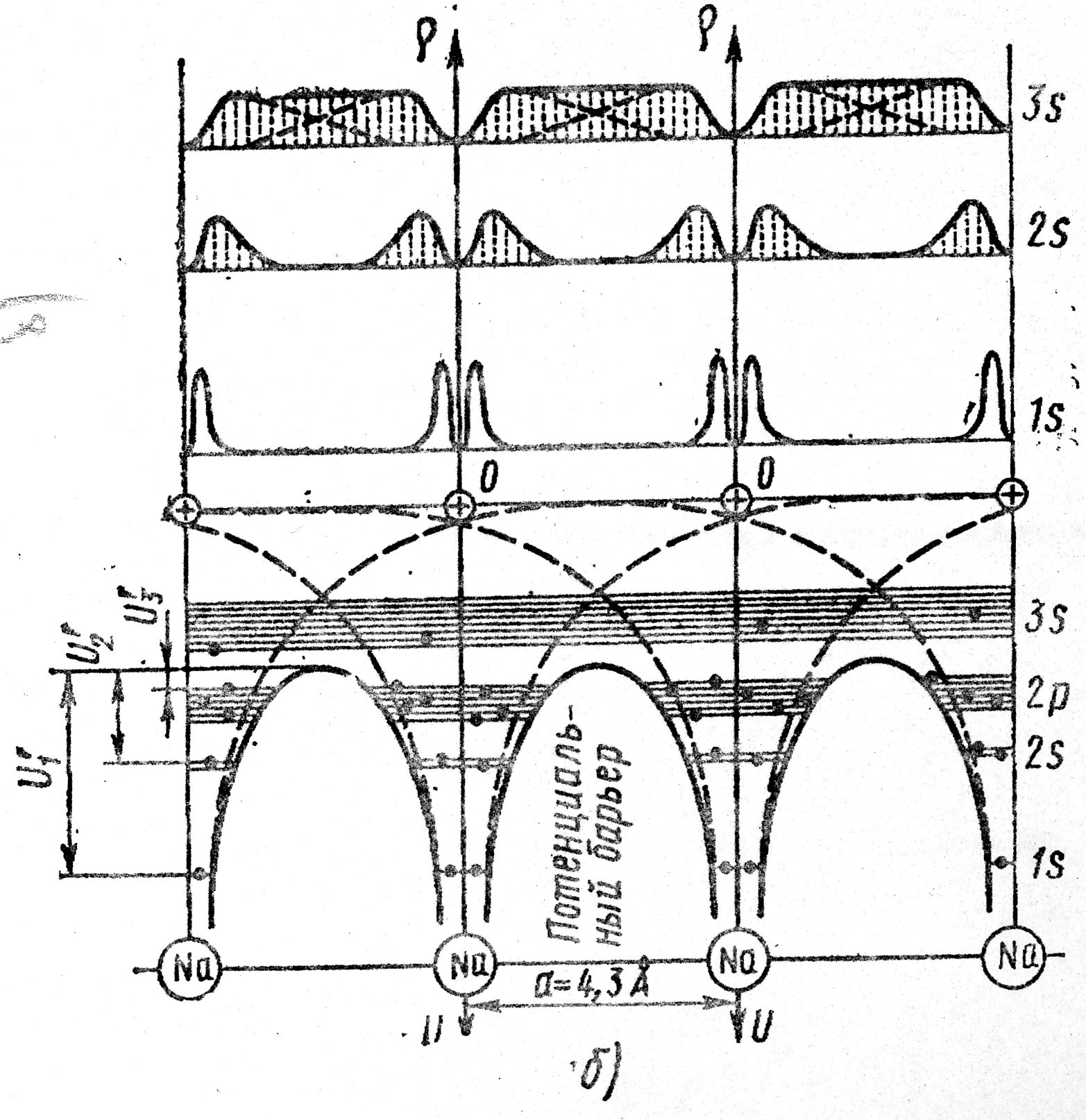При сближении атомов (медленным однородным сжатием без нарушения симметрии) взаимодействие между ними растет и при 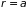достигает значений, характерных для кристалла (Рис. 4.5, б). Потенциальные кривые, отделяющие соседние атомы (пунктир), частично налагаются друг на друга и дают результирующие кривые, проходящие существенно ниже нулевого

Рис. 4.5

уровня изолированного атома. Таким образом, сближение атомов, во-первых, уменьшает потенциальный барьер до значения постоянной решетки , во-вторых, понижает его высоту. Появляется возможность для электронов (в основном, валентных) беспрепятственного перемещения по всему металлу.

4.6.3. Обоснование модели свободных электронов. Ни один электрон в металле не является независимым: они взаимодействуют друг с другом и с ионными остовами через интенсивные кулоновские силы. Тем не менее, существуют факторы, которые позволяют рассматривать обобществленные электроны как свободные. Во-первых, в среднем в пределах большого объема заряды ионов компенсируют заряды электронов. Электроны двигаются как бы на фоне положительного заряда, который нейтрализует их заряд. Во-вторых, при движении электрона в «море» себе подобных частиц его потенциал экранируется другими электронами. Это резко уменьшает область , в которой взаимодействие двух электронов играет существенную роль. В-третьих, из квантовой механики следует, что при наличии идеального периодического потенциала электроны не испытывают никакого сопротивления при движении. Сказанное объясняет и оправдывает широкое использование в теории металлов модели свободных электронов.

Наблюдаемое в реальных металлах сопротивление при движении электронов возникает из-за нерегулярностей (дефектов) в периодической структуре. Нерегулярности или дефекты могут быть различного рода, в том числе колебания атомов, вакансии, дислокации, примесные атомы. Регулярная ионная структура сказывается на инертных свойствах электрона, что учитывает уравнение Шредингера для волновой функции.

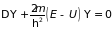. (4.34)

Здесь – полная энергия электрона, – потенциальная энергия, которая учитывает наличие ионного остова. В модели свободных электронов вводят вместо истинной массы электрона его эффективную массу , и рассматривается уравнение Шредингера в виде

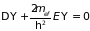. (4.35)

Волновая функция в этом случае определяет движение свободного электрона с эффективной массой .

4.6.4. Энергетические зоны и статистика электронного газа. По мере сближения атомов и образования решетки каждый атом попадает в поле соседей. Если в изолированном атоме энергетический уровень единственный, то в кристалле, состоящем из атомов, в силу их взаимодействия он повторяется раз, становится -кратно вырожденным. Такое перестановочное вырождение приводит к расщеплению уровня изолированного атома на близко расположенных подуровней, образующих энергетическую зону. Так, если энергетический уровень в атоме имел 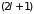-кратное вырождение, то соответствующая ему зона будет состоять из 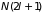подуровней. Расстояние между ними в обычных кристаллах очень мало. В кристалле объемом  м³ содержится 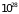атомов. При характерных ширинах зон  eV расстояние между подуровнями ничтожно мало (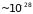  eV). Это дает основание считать их практически непрерывными, в конечном итоге заменять формулы с дискретными значениями энергии их непрерывным аналогом. Зоны разрешенных энергий, где могут находиться электроны, разделены запрещенными зонами. Последнюю полностью заполненную электронами называют валентной, следующую за ней (частично или полностью заполненную) – зоной проводимости. Например, в (Рис. 4.5) подуровни, относящиеся к , частично (наполовину) заполнены и принадлежат зоне проводимости, а подуровни – валентной зоне.

В кинетических явлениях (переносе тепла, заряда) принимают участие только те электроны, которые могут поглотить энергию от внешнего поля, т.е. перейти на свободный не занятый энергетический подуровень. Речь идет, как правило, об электронах, которые находятся либо в верхней части зоны проводимости (если она частично заполнена), либо в нижней, если она пустая (за счет электронов валентной зоны).

Расчет критерия невырожденности электронного газа дает

.

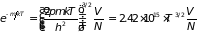Плотность свободных электронов в металле примерно равна 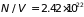 см^– 3. Тогда

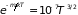
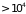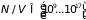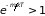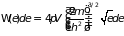откуда следует, что при всех температурах, кроме чрезвычайно высоких ( °К). В полупроводниках, где плотность электронов  см^– 3, и возможно применение классической статистики. Электронный газ в металлах описывается только квантовой статистикой, а именно: распределением Ферми-Дирака и плотностью состояний (см. раздел 2.1)