
- •1. Основные положения статистической термодинамики
- •1.1. Понятия и начала феноменологической термодинамики.
- •1.2. Микроскопическое (механическое) описание классических систем.
- •1.3. Особенности представления квантовых систем
- •1.4. Вероятность нахождения системы в элементе фазового пространства. Метод ансамблей Гиббса.
- •1.5. Макроскопические величины как фазовые средние
- •1.6. Распределение в системах с постоянным числом частиц
- •1.6.2. Распределения Гиббса.
- •1.6.3. Квазиклассическое приближение.
- •1.7. Свойства распределения Гиббса
- •1.8. Большое каноническое распределение Гиббса
- •2. Статистика идеального газа
- •2.1. Идеальный газ как модель статистической системы
- •2.2. Распределение Максвелла
- •2.3. Столкновения молекул со стенкой сосуда. Давление
- •2.4. Характерные величины идеального газа
- •2.5. Столкновение молекул между собой
- •2.6. Длина свободного пробега
- •2.7. Идеальный газ во внешнем поле
- •2.8. Число и функция состояний идеального газа
- •2.9. Классическая теория теплоемкости газа двухатомных молекул
- •2.10. Квантовая теория теплоемкости газа двухатомных молекул
- •2.11. Распределения в квантовых системах
- •3. Законы термодинамики
- •3.1. Статистическое обоснование первого начала термодинамики
- •3.2. Второе начало термодинамики
- •3.3. Вечный двигатель второго рода. Максимальная работа процессов
- •3.4. Полезная работа тепловых машин
- •3.5. Метод термодинамических потенциалов
- •3.6. Термодинамические коэффициенты. Критерии устойчивости равновесия
- •3.7. Статистическое вычисление термодинамических величин
- •3.8. Третье начало термодинамики (теорема Нернста)
- •3.9. Применения термодинамики
- •4. Статистика сложных систем.
- •4.1. Модель кристаллического твердого тела. Уравнение движения атомов
- •4.2. Дисперсионное уравнение нормальных колебаний кристалла
- •4.3. Кристалл как система линейных гармонических осцилляторов
- •4.4. Статистическая сумма и энергия кристалла (в гармоническом приближении)
- •4.5. Теория теплоемкости Дебая
- •4.6. Электронный газ в металлах
- •4.7. Зависимость энергии электрона от волнового вектора. Эффективная масса
- •4.8. Теория парамагнетизма. Природа и характеристики магнетизма.
- •4.9. Равновесное излучение.
- •4.10. Системы с кулоновским взаимодействием частиц.
- •5. Теория малых флуктуаций
- •5.1. Определение и значение флуктуаций
- •5.2. Мера вероятности и масштаб флуктуаций
- •5.3. Флуктуации термодинамических величин в однородной среде
- •5.4. Предельная чувствительность измерительных приборов
- •5.5. Рассеяния света флуктуациями
- •6. Элементы теории физической кинетики
- •6.1. Определения и характеристики необратимых процессов
- •6.2. Теория стационарных процессов в газе свободных электронов
- •6.3. Газокинетическое уравнение Больцмана
- •6.4. Приближение времени релаксации
- •Раздел 2
- •Раздел 2
- •Раздел 3
- •Раздел 4
- •Раздел 5
- •Раздел 6
- •Список Литературы
5.2. Мера вероятности и масштаб флуктуаций
5.2.1. Флуктуации
в замкнутых системах. Пусть замкнутая
система в состоянии статистического
равновесия имеет энтропию
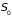 .
При переходе в неравновесное состояние
энтропия принимает значение
.
Считаем, что изменение состояния системы
обусловлено изменением некоторого
внутреннего параметра
.
При переходе в неравновесное состояние
энтропия принимает значение
.
Считаем, что изменение состояния системы
обусловлено изменением некоторого
внутреннего параметра
 (например, плотности, давлении), значение
которого зависит от состояния всей
системы, а в состоянии равновесия
(например, плотности, давлении), значение
которого зависит от состояния всей
системы, а в состоянии равновесия
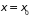 .
Энтропия системы
.
Энтропия системы
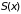 – функция параметра
.
Согласно формуле Больцмана (
– функция параметра
.
Согласно формуле Больцмана (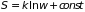 ),
вероятность величины
иметь значение в интервале между
и
),
вероятность величины
иметь значение в интервале между
и
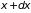 равна
равна
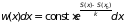 . (5.1)
. (5.1)
Эта
формула была впервые применена А.
Эйнштейном в 1910 г. к исследованию
флуктуаций. Здесь в качестве меры
вероятности
флуктуации рассматривается изменение
энтропии. В состоянии равновесия энтропия
имеет максимальное значение
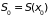 ,
поэтому разность энтропии
,
поэтому разность энтропии
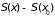 отрицательная. Считаем отклонение
параметра
от его равновесного значения малым.
Представляя
рядом по степеням
и ограничиваясь членом второго порядка
малости, получим с учетом
отрицательная. Считаем отклонение
параметра
от его равновесного значения малым.
Представляя
рядом по степеням
и ограничиваясь членом второго порядка
малости, получим с учетом
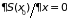
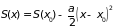 ,
,
где
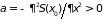 .
Нормировочную постоянную определим из
условия
.
Нормировочную постоянную определим из
условия
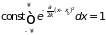 .
.
Хотя здесь
использовалось выражение для
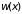 ,
относящееся к малым отклонениям от
,
относящееся к малым отклонениям от
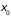 ,
но ввиду быстрого убывания подынтегральной
функции с увеличением
,
но ввиду быстрого убывания подынтегральной
функции с увеличением
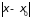 область интегрирования можно распространить
на все значения от
область интегрирования можно распространить
на все значения от
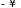 до
до
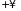 .
После интегрирования получим
.
После интегрирования получим
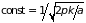 .
Таким образом, вероятность отклонения
от
определяется распределением Гаусса:
.
Таким образом, вероятность отклонения
от
определяется распределением Гаусса:
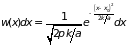 , (4.2)
, (4.2)
а величина
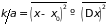 есть дисперсия (средний квадрат
отклонения); ее еще называют центральным
моментом второго порядка. Если в
разложении
учитывать последующие члены, то
распределение вероятностей флуктуации
становится негауссовым и может быть
нессиметричным. В этом случае требуется,
помимо дисперсии, задание моментов
более высокого порядка.
есть дисперсия (средний квадрат
отклонения); ее еще называют центральным
моментом второго порядка. Если в
разложении
учитывать последующие члены, то
распределение вероятностей флуктуации
становится негауссовым и может быть
нессиметричным. В этом случае требуется,
помимо дисперсии, задание моментов
более высокого порядка.
Из формулы следует,
что отклонения физического параметра
от
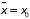 гораздо чаще встречается в интервале
гораздо чаще встречается в интервале
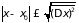 ,
чем вне его. Величина
,
чем вне его. Величина
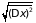 дает представление о масштабе
флуктуаций.
дает представление о масштабе
флуктуаций.
Знание среднего
квадрата отклонения
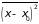 позволяет найти дисперсию для любой
функции случайной величины
позволяет найти дисперсию для любой
функции случайной величины
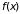 .
Учитывая малую величину отклонения,
имеем
.
Учитывая малую величину отклонения,
имеем
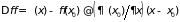 .
Откуда следует
.
Откуда следует
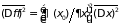 .
.
Заметим, что приведенная формула (5.2) применима к флуктуациям в системах с постоянной энергией.
5.2.2. Флуктуации
в квазизамкнутых системах. Произвольную
квазизамкнутую систему можно рассматривать
как малую часть замкнутой системы или
как подсистему, погруженную в термостат
с постоянной температурой
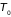 .
Считаем, что флуктуации происходят
только в подсистеме, тогда как термостат
остается равновесной системой. Состояние
подсистемы определяется некоторым
внешним параметром
.
При переходе из равновесного в
неравновесное состояние он меняется
от
.
Считаем, что флуктуации происходят
только в подсистеме, тогда как термостат
остается равновесной системой. Состояние
подсистемы определяется некоторым
внешним параметром
.
При переходе из равновесного в
неравновесное состояние он меняется
от
 до
,
при этом изменяются и термодинамические
параметры, характеризующие подсистему.
Предполагаем изменения
настолько медленным, что в каждый данный
момент времени подсистема находится в
равновесном состоянии, и ее термодинамические
параметры связаны между собой равновесными
соотношениями. Причиной перехода
подсистемы из равновесного в неравновесное
состояние будем считать действие
некоторого внешнего теплоизолированного
источника работы. При изменении параметра
на величину
до
,
при этом изменяются и термодинамические
параметры, характеризующие подсистему.
Предполагаем изменения
настолько медленным, что в каждый данный
момент времени подсистема находится в
равновесном состоянии, и ее термодинамические
параметры связаны между собой равновесными
соотношениями. Причиной перехода
подсистемы из равновесного в неравновесное
состояние будем считать действие
некоторого внешнего теплоизолированного
источника работы. При изменении параметра
на величину
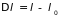 источник совершает работу
источник совершает работу
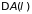 .
.
Поскольку
термостат, подсистема и источник работы
составляют замкнутую систему, к ним
применима формула (5.1), где общее изменение
энтропии состоит из изменения энтропии
подсистемы
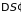 и термостата
и термостата
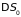 :
:
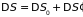 .
.
Поэтому вероятность перехода подсистемы в состояние с под действием внешнего источника роботы определяется формулой
 . (5.3)
. (5.3)
Запишем основные термодинамические равенства для подсистемы и термостата
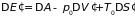
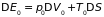 .
.
Здесь
и
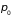 – равновесные значения температуры и
давления подсистемы и термостата,
– равновесные значения температуры и
давления подсистемы и термостата,
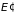 и
и
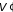 – энергия и объем подсистемы,
– работа внешнего источника (но не
термостата!). Поскольку внутренняя
энергия и полный объем замкнутой системы
остаются постоянными (
– энергия и объем подсистемы,
– работа внешнего источника (но не
термостата!). Поскольку внутренняя
энергия и полный объем замкнутой системы
остаются постоянными (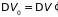 ,
,
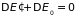 ),
то из указанных равенств следует
),
то из указанных равенств следует
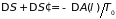 .
.
Подстановка этих величин в (5.3) дает
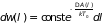 . (5.4)
. (5.4)
В
самом общем случае мерой вероятности
малых флуктуаций в макроскопической
системе есть работа, которую нужно над
нею совершить для изменения параметра
,
характеризующего состояние системы,
на величину
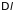 .
Это не означает, что флуктуация происходит
в результате воздействия (работы)
внешнего источника. Так, в замкнутой
системе (
.
Это не означает, что флуктуация происходит
в результате воздействия (работы)
внешнего источника. Так, в замкнутой
системе ( ,
,
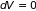 )
при равновесном процессе из основного
термодинамического равенства (
)
при равновесном процессе из основного
термодинамического равенства (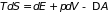 )
следует
)
следует
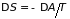 .
Здесь
– работа, совершаемая над системой, не
связана с изменением ее объема (например,
это передвижение внутренних перегородок).
Как в замкнутой, так и незамкнутой
системах работа
является лишь количественной
характеристикой флуктуации.
.
Здесь
– работа, совершаемая над системой, не
связана с изменением ее объема (например,
это передвижение внутренних перегородок).
Как в замкнутой, так и незамкнутой
системах работа
является лишь количественной
характеристикой флуктуации.
Работу
можно представить как изменение
потенциальной энергии
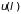 при перемещении системы в некотором
воображаемом (а иногда и реальном) поле
сил
при перемещении системы в некотором
воображаемом (а иногда и реальном) поле
сил
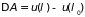 .
.
Заменяя работу в (5.4) на изменение потенциальной энергии, получаем формулу
 , (5.5)
, (5.5)
которая является
аналогом формулы Больцмана. В силу
малости флуктуаций
можно разложить в ряд по малому параметру
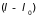
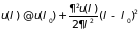 .
.
Здесь учтено, что
в состоянии равновесия потенциальная
энергия должна иметь минимум (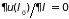 ),
а
),
а
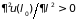 .
Поэтому распределение вероятностей
флуктуаций и в незамкнутых системах
определяется функцией Гаусса:
.
Поэтому распределение вероятностей
флуктуаций и в незамкнутых системах
определяется функцией Гаусса:
 .
.
Значение второй
производной
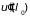 зависит
от природы поля сил, в котором происходит
«перемещение» системы из положения
в
.
Общим свойством вероятностей флуктуаций
в замкнутых и незамкнутых системах
является резкое уменьшение их с ростом
ее величины, а также с уменьшением ее
дисперсии. Поскольку последняя
пропорциональна температуре, то
интенсивность (масштаб) флуктуаций
уменьшается с падением температуры.
зависит
от природы поля сил, в котором происходит
«перемещение» системы из положения
в
.
Общим свойством вероятностей флуктуаций
в замкнутых и незамкнутых системах
является резкое уменьшение их с ростом
ее величины, а также с уменьшением ее
дисперсии. Поскольку последняя
пропорциональна температуре, то
интенсивность (масштаб) флуктуаций
уменьшается с падением температуры.
