
- •1. Основные положения статистической термодинамики
- •1.1. Понятия и начала феноменологической термодинамики.
- •1.2. Микроскопическое (механическое) описание классических систем.
- •1.3. Особенности представления квантовых систем
- •1.4. Вероятность нахождения системы в элементе фазового пространства. Метод ансамблей Гиббса.
- •1.5. Макроскопические величины как фазовые средние
- •1.6. Распределение в системах с постоянным числом частиц
- •1.6.2. Распределения Гиббса.
- •1.6.3. Квазиклассическое приближение.
- •1.7. Свойства распределения Гиббса
- •1.8. Большое каноническое распределение Гиббса
- •2. Статистика идеального газа
- •2.1. Идеальный газ как модель статистической системы
- •2.2. Распределение Максвелла
- •2.3. Столкновения молекул со стенкой сосуда. Давление
- •2.4. Характерные величины идеального газа
- •2.5. Столкновение молекул между собой
- •2.6. Длина свободного пробега
- •2.7. Идеальный газ во внешнем поле
- •2.8. Число и функция состояний идеального газа
- •2.9. Классическая теория теплоемкости газа двухатомных молекул
- •2.10. Квантовая теория теплоемкости газа двухатомных молекул
- •2.11. Распределения в квантовых системах
- •3. Законы термодинамики
- •3.1. Статистическое обоснование первого начала термодинамики
- •3.2. Второе начало термодинамики
- •3.3. Вечный двигатель второго рода. Максимальная работа процессов
- •3.4. Полезная работа тепловых машин
- •3.5. Метод термодинамических потенциалов
- •3.6. Термодинамические коэффициенты. Критерии устойчивости равновесия
- •3.7. Статистическое вычисление термодинамических величин
- •3.8. Третье начало термодинамики (теорема Нернста)
- •3.9. Применения термодинамики
- •4. Статистика сложных систем.
- •4.1. Модель кристаллического твердого тела. Уравнение движения атомов
- •4.2. Дисперсионное уравнение нормальных колебаний кристалла
- •4.3. Кристалл как система линейных гармонических осцилляторов
- •4.4. Статистическая сумма и энергия кристалла (в гармоническом приближении)
- •4.5. Теория теплоемкости Дебая
- •4.6. Электронный газ в металлах
- •4.7. Зависимость энергии электрона от волнового вектора. Эффективная масса
- •4.8. Теория парамагнетизма. Природа и характеристики магнетизма.
- •4.9. Равновесное излучение.
- •4.10. Системы с кулоновским взаимодействием частиц.
- •5. Теория малых флуктуаций
- •5.1. Определение и значение флуктуаций
- •5.2. Мера вероятности и масштаб флуктуаций
- •5.3. Флуктуации термодинамических величин в однородной среде
- •5.4. Предельная чувствительность измерительных приборов
- •5.5. Рассеяния света флуктуациями
- •6. Элементы теории физической кинетики
- •6.1. Определения и характеристики необратимых процессов
- •6.2. Теория стационарных процессов в газе свободных электронов
- •6.3. Газокинетическое уравнение Больцмана
- •6.4. Приближение времени релаксации
- •Раздел 2
- •Раздел 2
- •Раздел 3
- •Раздел 4
- •Раздел 5
- •Раздел 6
- •Список Литературы
2.8. Число и функция состояний идеального газа
2.8.1. Число
состояний и критерий невырожденности.
Для расчета числа состояний моделируем
идеальный газ квазиклассической
системой. Каждому состоянию свободной
частицы в фазовом пространстве (три
степени свободы,
)
отвечает элементарная ячейка объемом
(
– постоянная Планка). Объем фазового
пространства, которому соответствует
в координатном пространстве объем
,
где может находиться частица, а импульс
изменяется в интервале от
до
,
равен
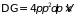 .
Тогда число состояний определяется
формулой
.
Тогда число состояний определяется
формулой
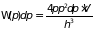 , (2.31.а)
, (2.31.а)
или, учитывая связь между энергией частицы и импульсом ( ),
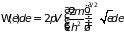 . (2.31.б)
. (2.31.б)
Плотность числа
состояний свободной частицы пропорциональна
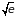 .
Если в качестве частицы рассматривать
электрон, который имеет в каждой ячейке
два состояния, отличающиеся направлением
спина, число его состояний удваивается,
.
Если в качестве частицы рассматривать
электрон, который имеет в каждой ячейке
два состояния, отличающиеся направлением
спина, число его состояний удваивается,
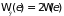 .
Формулы легко обобщаются на системы с
произвольным числом степеней свободы
.
Формулы легко обобщаются на системы с
произвольным числом степеней свободы
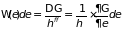 .
.
Общее число
состояний свободной частицы в интервале
энергий от
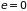 до
до
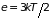 определяется интегралом
определяется интегралом
 . (2.32)
. (2.32)
При числе частиц в объеме критерий невырожденности принимает вид
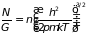 . (2.33)
. (2.33)
Для одноатомного
молекулярного газа, например, азота при
нормальных условиях (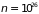 м–3,
м–3,
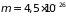 кг,
кг,
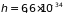 Дж·с,
Дж·с,
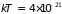 Дж)
Дж)
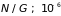 .
Такие малые значения критерия
свидетельствуют, что обычные молекулярные
газы в нормальных условиях являются
невырожденными и описываются статистикой
Максвелла-Больцмана. Электронный газ
в металлах (
.
Такие малые значения критерия
свидетельствуют, что обычные молекулярные
газы в нормальных условиях являются
невырожденными и описываются статистикой
Максвелла-Больцмана. Электронный газ
в металлах ( м–3,
м–3,
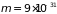 кг)
оказывается вырожденным вплоть до
температур
кг)
оказывается вырожденным вплоть до
температур
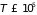 К
(
К
( )
и в реальных условиях подчиняется
квантовой статистике Ферми-Дирака.
Невырожденное состояние электронного
газа может быть достигнуто уменьшением
концентрации
.
Уже при
)
и в реальных условиях подчиняется
квантовой статистике Ферми-Дирака.
Невырожденное состояние электронного
газа может быть достигнуто уменьшением
концентрации
.
Уже при
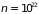 м–3
критерий
м–3
критерий
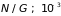 .
Такая и меньшая концентрация электронов
имеет место в невырожденных полупроводниках.
.
Такая и меньшая концентрация электронов
имеет место в невырожденных полупроводниках.
2.8.2. Функция
распределения идеального газа суть
плотность частиц
в данном состоянии. Связь между
термодинамическими параметрами системы
и характеристиками микрочастиц задается
полной статистической функции
распределения
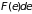 ,
имеющей смысл числа частиц с энергией
от
до
.
Её можно представить произведением
числа состояний
на вероятность их заполнения:
,
имеющей смысл числа частиц с энергией
от
до
.
Её можно представить произведением
числа состояний
на вероятность их заполнения:
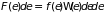 .
Функцию
.
Функцию
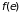 называют функцией распределения.
Кроме вероятности заполнения состояний,
она имеет смысл среднего числа частиц,
приходящегося на одно состояние. Из
известных распределений Максвелла
называют функцией распределения.
Кроме вероятности заполнения состояний,
она имеет смысл среднего числа частиц,
приходящегося на одно состояние. Из
известных распределений Максвелла
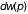 и
для импульсов и энергий одноатомной
молекулы (2.5) и (2.7) нетрудно получить
число соответствующих свободных молекул
в объеме
и
для импульсов и энергий одноатомной
молекулы (2.5) и (2.7) нетрудно получить
число соответствующих свободных молекул
в объеме
 ,
т.е. полную функцию распределения:
,
т.е. полную функцию распределения:
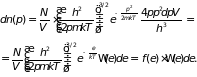 (2.34)
(2.34)
Функция распределения
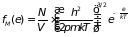 (2.35)
(2.35)
получила название функция распределения Максвелла-Больцмана. Её можно записать и в другом виде – в форме распределения Гиббса для системы с переменным числом частиц, для чего воспользуемся тождеством
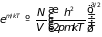 . (2.36)
. (2.36)
Распределение Максвелла-Больцмана принимает вид
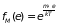 . (2.37)
. (2.37)
Введенный здесь параметр
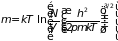 , (2.38)
, (2.38)
как будет показана в следующих разделах, является химическим (парциальным) потенциалом.
2.8.3. Функция (интеграл) состояний. Согласно определению, функция состояний идеального одноатомного газа в квазиклассическом приближении имеет вид
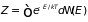 . (2.39)
. (2.39)
Поскольку все частицы газа являются независимыми, то
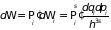 ,
,
где произведение берется по всем координатам и импульсам частиц. Штрих в произведении означает, что при его образовании следует включать в него только такие члены, которые отвечают различным состояниям системы в целом. Последующее интегрирование ведется по соответствующим областям фазового пространства
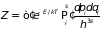 .
.
Если бы молекулы
в газе отличались друг от друга, то
определенным значениям импульса и
координаты частиц соответствовало одно
состояние газа, т.е.
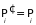 .
Но частицы однородного газа – молекулы,
атомы ничем не отличаются друг от друга.
.
Но частицы однородного газа – молекулы,
атомы ничем не отличаются друг от друга.
Для определения
области интегрирования рассмотрим
случай двух частиц. Пусть первая частица
имеет импульс
 и координату
и координату
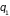 ,
а вторая –
,
а вторая –
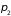 и
и
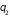 .
В силу тождественности частиц состояние
системы не изменится, если значения
импульса и координаты второй молекулы
станут равными первой и наоборот. В
такой системе из двух частиц следует
интегрировать по всем состояниям –
координатам и импульсам двух частиц
(
,
,
,
),
но полученный результат уменьшить
вдвое. При этом автоматически будет
учтено, что «перестановка» в фазовом
пространстве изобразительных точек
(состояний частиц) не приводит к разным
состояниям системы.
.
В силу тождественности частиц состояние
системы не изменится, если значения
импульса и координаты второй молекулы
станут равными первой и наоборот. В
такой системе из двух частиц следует
интегрировать по всем состояниям –
координатам и импульсам двух частиц
(
,
,
,
),
но полученный результат уменьшить
вдвое. При этом автоматически будет
учтено, что «перестановка» в фазовом
пространстве изобразительных точек
(состояний частиц) не приводит к разным
состояниям системы.
Полученный результат
обобщается на произвольные состояния
газа, содержащего
тождественных молекул. Можно сказать,
что совокупность всех состояний, которые
получаются перестановкой между собой
изобразительных точек в фазовом
пространстве, являются тождественными
физическими состояниями – отвечают
только одному физическому состоянию.
Поэтому при выполнении интегрирования
по всем возможным значениям координат
и импульсов молекул нужно разделить
результат на число перестановок
изобразительных точек между собой, т.е.
на
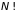 .
В частном случае для двух молекул
.
В частном случае для двух молекул
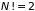 .
Итак можно записать
.
Итак можно записать
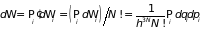 .
.
Соответственно для функции состояний имеем:
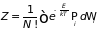 , (2.40)
, (2.40)
где интегрирование
ведется по всему фазовому пространству.
Учитывая, что полная энергия идеального
газа равна сумме энергий составляющих
его молекул
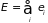 ,
находим
,
находим
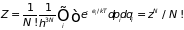 (2.41)
(2.41)
где
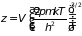 – ранее определенный интеграл состояний
одной молекулы, поэтому
– ранее определенный интеграл состояний
одной молекулы, поэтому
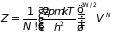 . (2.42)
. (2.42)
Через эту функцию состояний находятся все термодинамические потенциалы, а следовательно, свойства идеального газа как системы, подчиняющейся классической статистике.
