§1. Векторное пространство многочленов над полем p коэффициентов

Как мы видели (книга 2, гл.3, §1) сложение на множестве многочленов над полем Р наделено внутренним законом коммутативной группы. Теперь определим на множестве Рх многочленов при помощи поля Р внешний закон композиции.

Умножение на элемент из Р. Пусть Р; положим f(х) есть многочлен, все коэффициенты которого суть произведения элемента  на коэффициенты многочлена f(х).

Очевидно, что иимеем:

, где = 1 – нейтральный элемент умножения в Р.

Таким образом, операции сложения многочленов и умножение его на число из Р превращают множество Рх многочленов в векторное пространство над полем Р коэффициентов, а многочлен по отношению к этому множеству – это вектор и его можно обозначать .

§2. Векторные пространства р n над полем р

Любое поле Р (поле R действительных или С комплексных чисел) является векторным пространством над самим собой со сложением в качестве внутреннего закона и умножением в качестве внешнего (К = L = Р).

Произведение любого конечного числа n множеств Р есть также векторное пространство над полем Р. Обозначается это векторное пространство Элементами (векторами) этого пространства являются упорядоченные наборы изn чисел (_, _, . . ., _n), называемые компонентами или координатами вектора:= (_,_, . . .,_n), где, аВнутренний и внешний законы композиции в этом пространстве имеют вид:

, (4.1)

здесь

В принципе компоненты вектора могут располагаться не только строкой , но и столбцом.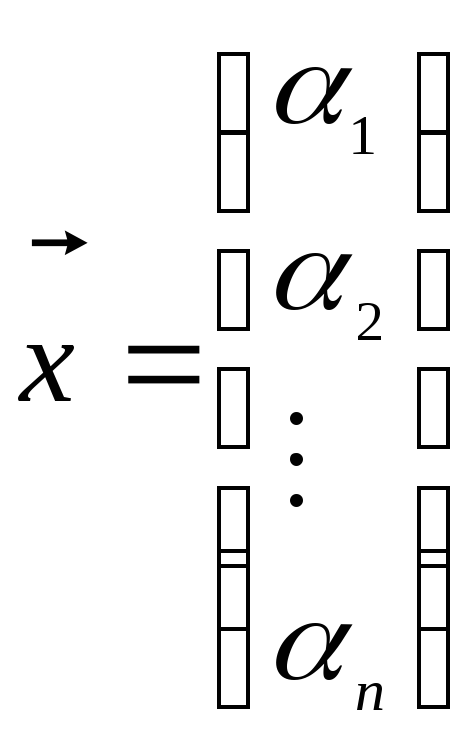

В зависимости от расположения эти пространства называются пространством вектор-строк длиной n, либо вектор-столбцов высотой n.

Рассмотрим случай, когда P = R и векторные пространства Pⁿ = Rⁿ вещественные (действительные). Если n = 1,2,3, то, как мы уже выяснили, между множеством точек арифметического пространства Rⁿ и множеством точек ориентированного геометрического пространства можно установить взаимно однозначное отображение, обладающее наглядностью: R¹ множество точек координатной оси; R²  множество точек координатной плоскости; R³  множество точек ориентированного геометрического пространства. Под отображением здесь понимается способ определения координат точек пространства.

По аналогии естественно предположить, что в геометрическом пространстве существуют и наглядные векторные пространства, которые можно поставить во взаимно однозначное соответствие с векторными пространствами Rⁿ над полем R, где n = 1, 2, 3. Установим такое соответствие.

§3. Векторы в геометрическом пространстве

Определение. Вектором в геометрическом пространстве называется направленный отрезок, который задается упорядоченной парой точекА и В. Первая точка А называется началом направленного отрезка , а вторая точкаВ – его концом: =.

В обозначение направленного отрезка порядок точек определяется порядком их записи:А – первая точка, В – вторая. Если точки А и В различны, то направленный отрезокназывается ненулевым (илиневырожденным), а если точки А и В совпадают, то направленный отрезок называется нулевым (иливырожденным) и обозначается .

Длина направленного отрезка, характеризующая численное значение вектора, называется модулем или абсолютной величиной вектора и обозначается или. Направление отрезка определяет прямую, на которой располагается вектор. Если векторы расположены на одной прямой, или на параллельных прямых, то такие векторы называютсяколлинеарными, т.е. существует прямая которой они параллельны. Если существует плоскость, относительно которой векторы параллельны, то такие векторы называются компланарными.

Нулевой вектор считается коллинеарным любому вектору, так как он не имеет определенного направления. Длина его равна нулю.

Равенство векторов. Два вектора считаются равными, если равны их направленные отрезки. Для равенства направленных отрезков можно дать три различных определения. В зависимости от этого вектора подразделяются на три типа.