§8. Линейные отображения векторных пространств

Определение 1. Пусть имеются два векторных пространства K и L над одним и тем же полем Р. Линейным отображением пространства К в L называется отображение f :  L , обладающее следующими свойствами:

Образы

Следует подчеркнуть, что сложение в правой и левой частях первой из формул обозначают две, вообще говоря, различные операции: сложение в пространстве К и в пространстве L. Аналогичное замечание относится и ко второй формуле.

Определение 2. Если L = P, то значение отображения есть число из P; в этом случае говорят, что f есть линейная форма.

Так, ортогональная проекция свободного вектора на плоскость есть линейное отображение пространства R³ в R².

Следствие из определения 1. Рассмотрим множество f (K), т.е. множество элементов из L, которые служат при отображении f образами, по крайней мере, одного элемента .f (K) есть векторное пространство, являющееся векторным подпространством пространства L и размерность пространства f (K) не превосходит размерности К. Действительно если линейно зависимы вК, то в Р существуют такие , не все равные нулю, что, но тогда,

и так элементы тоже линейно зависимы. Обратное, вообще говоря, неверно. Здесь учтено, что . Это следует из линейности отображения: и, значит,Необходимо однако отметить, чтовив правой части равенства отличаются, так как это нейтральные элементы, принадлежащие разным множествам.

8.1. Ранг линейного отображения

Определение. Рангом r линейного отображения f : K  L называется размерность векторного пространства f(K). Если K имеет размерность n, то, поскольку размерность пространства f(K) не может превосходить n, находим, что r ≤ n.

Если есть базис пространстваК, то иТаким образом, векторное пространствоf (K) порождается векторами и, следовательно,r есть максимальное число линейно независимых векторов т.е. ранг данной системы векторов.

Если все векторы линейно независимы и составляют базисf (K), а f (K) исчерпывает все пространство L (т.е. f (K) = L), то отображение f будет взаимно однозначным. Следовательно, для того, чтобы линейное отображение f было взаимно однозначным, необходимо и достаточно, чтобы dimK = dimL = n, и равнялось рангу r отображения. Таким образом, взаимно однозначные отображения возможны только между пространствами одинаковой размерности.

Заметим, что если линейное отображение f – взаимно однозначно, то оно будет изоморфизмом.

8.2. Координатная запись линейных отображений

Рассмотрим два векторных пространства K и L различных размерностей над одним и тем же полем P. Пусть в пространстве K размерности m выбран базис , а в пространстве L размерности h – базис . Пусть далееf есть линейное отображение K в L; оно переводит   в  L. Разложив векторы ипо базисам соответствующих пространств, получим

, иили с учетом свойства линейного отображения, имеем

Так как элементы , то при помощи базисаих можно представить в виде

или

Следовательно,

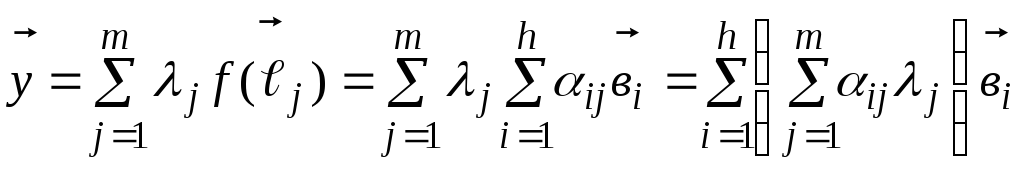или покоординатно, с учетом, что

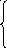
 _ = _ _ +  _2 ₂ + . . . +  _m _m,

 ₂ = _2 _ +  ₂₂ ₂ + . . . +  _2m _m, (4.9)

_{. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .}

 _h = _h _ +  _h2 ₂ + . . . +  _hm _m.

Следует отметить, что данная система содержит элементы _j, _i и _ij, принадлежащие только полю Р. Это позволяет рассматривать указанную систему и как характеристику линейного отображения пространства P^m в P^h. Элементами пространства P^m являются вектора , а пространстваP^h – вектора Таким образом, любому линейному отображениюf векторного пространства К в L можно сопоставить линейное отображение пространства P^m в P^h, которое будет определяться одинаковыми выражениями, характеризующих отображение.

Полученная система выражений в полной мере характеризует линейное отображение f векторного пространства К в L. В свою очередь эта система задана, если известна прямоугольная таблица коэффициентов _ij, записываемая следующим образом;

 __2 . . .  _m i = 1,2,...,h,

А =  _2 ₂₂ . . .  _2m = (_ij),

_{. . . . . . . . . . . . . . . . .} . j = 1,2,...,m

_h _h2 . . .  _hm

Такая прямоугольная таблица чисел называется матрицей, а числа _ij называются ее элементами.

Множество элементов, имеющих одинаковые первые индексы, называются строкой, а множество элементов, имеющих одинаковые вторые индексы, называются столбцом. Так, _ij есть элемент i-й строки и j-го столбца.

С помощью матрицы А систему выражений (4.9), характеризующих линейное отображение f векторного пространства К в L (или P^m в P^h ) записывают в следующем виде где

Матрицу можно рассматривать и независимо от пространств К и L. Ее можно ассоциировать с заданием системы векторов в пространстве вектор-строк, либо в пространстве вектор-столбцов. Действительно, пусть элементы i-й строки матрицы (_i1, _i2, . . . _im ) представляют собой компоненты вектор-строки в пространствеP^m , тогда

__2 . . . _m

А = _2₂₂ . . . _2m = (4.10)

_{. . . . . . . . . . . . . . . . . :}

_h_h2 . . . _hm

и, следовательно, задание матрицы А означает задание системы из h вектор-строк в пространствеР^m. Аналогично,

_ij _ _2 . . . _m

= _j   ^h, тогда А = _2 ₂₂ . . . _2m = () (4.11)

_{: . . . . . . . . . . . . . . . . .}

_hj _h _h2 . . . _hm

Следовательно, задание матрицы А означает задание системы из m вектор-столбцов в пространстве P^h.

Элементами матрицы в этих случаях являются компоненты векторов.

Если матрицу А в выражении (4.9) рассматривать как заданную систему вектор-столбцов в пространстве P^h, то формулы (4.9) можно записать в следующей эквивалентной форме:

,

₁ _1j

здесь =_ Р^h, = _j Р^h, j = 1,2,..., m.

: :

_h _hj

Это выражение означает, что вектор является линейной комбинацией системы вектор-столбцов из P ^h , заданных матрицей А с коэффициентами _   , _m. Из выше изложенного ясно, что матрицу можно рассматривать отдельно как самостоятельную величину, и на множестве матриц, как и на любом множестве, вводить свои внутренние и внешние законы композиции.