§5. Тригонометрическая форма комплексного числа. Формула муавра. Извлечение корня

Рассмотрим отличное от нуля комплексное число z = а + iв, и запишем его, используя значение |z| = d(ОМ ) и φ = Аrg z. Воспользовавшись, рис.2.1, можем записать, а = |z| cos и в = |z|sin . Тогда для комплексного числа получаем:

z = |z|(cosφ +i sinφ) или z = r (cosφ +i sinφ), где r = |z|. (2.5)

Эта запись называется тригонометрической формой комплексного числа. Для z = 0 тригонометрическая форма не определена, и за аргумент можно взять любое действительное число.

Использование тригонометрической формы комплексного числа значительно упрощает операции умножения, деления и извлечения корня.

Умножение. Пусть z₁ · z₂  0

и z₁ = r₁ (cosφ₁ +i sinφ₁), а z₂ = r₂ (cosφ₂ +i sinφ₂). Тогда

z₁ · z₂ = r₁r₂(cosφ₁ +i sinφ₁)(cosφ₂ +i sinφ₂) =

= r₁r₂ [(cosφ₁ cosφ₂ – sinφ₁ sinφ₂) + i (sinφ₁ cosφ₂ + cosφ₁ sinφ₂ )] =

= r₁r₂ [cos(φ₁ +φ₂) + i sin(φ₁ + φ₂)].

Таким образом, произведение двух комплексных чисел, отличных от нуля, есть комплексное число, модуль которого равен произведению модулей этих чисел, а аргумент равен сумме аргументов перемноженных чисел. Полученный результат легко перенести на произведение n чисел z₁, z₂, . . ., z_n. В частности если z₁ = z₂ = . . .= z_n = z = r (cosφ +i sinφ), то

zⁿ = rⁿ(cos nφ +i sin nφ). (2.6)

Это равенство называется формулой Муавра. Отсюда

|zⁿ| = |z|ⁿ, Arg zⁿ = n Arg z.

Деление.

.

Равенство возможно, если

.

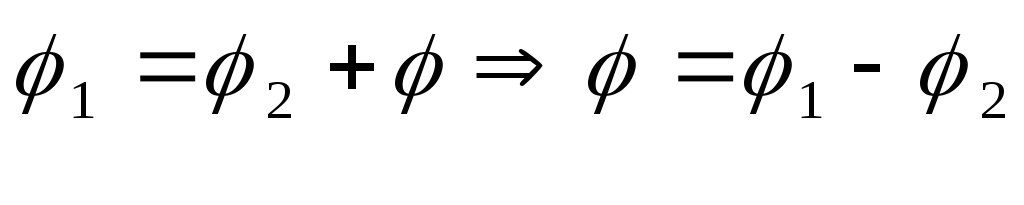Частное двух комплексных чисел, отличных от нуля, есть комплексное число, модуль которого равен частному модулей данных чисел, а аргумент – разнице аргументов числителя и знаменателя.

Извлечение корня. Корнем n-ой степени из комплексного числа z называется любое число z_kС, n-ая степень которого равна z. Таким образом, . Из последнего равенства имеем:

и . Следовательно, и .

Если z = 0, то непременно z_к = 0 и значит, ноль имеет в С только один корень n-ой степени, а именно ноль.

Теперь допустим, что z  0. Поскольку Arg z определен с точностью до 2, и поэтому аргумент числа z_к может принимать n, и только n значений, определенных с точностью до 2, а именно:

, где к = 0, 1, 2, . . ., n – 1.

Следовательно, имеет на множестве С п различных значений z₀, z₁, . . . , z_n-1, п-ая степень которых равна z: , к = 0, 1, 2, . . ., n – 1.

. (2.7)

Ясно, что точки, отображающие числа z_к на комплексной плоскости, лежат на окружности с центром О и радиусом и представляют собой вершины правильного n-угольника.

Рассмотрим частный случай, когда z = 1; тогда |z| = 1, аrg z = 0,

, m =0, ±1, ±2, . . . и, значит, корни n-ой степени из единицы имеют модуль 1, а аргумент гдек = 0, 1, 2, . . . , n – 1. Стало быть, корнями единицы на множестве С будут числа:

где к = 0, 1, 2, . . . , n – 1, m = 0, ±1, ±2, . . . .

Точки, отображающие числа z_к на комплексной плоскости для случая n = 6 показаны на рис.2.2.

=/3

Рис. 2.2