3.2. Определенная квадратичная форма. Критерий Сильвестра

Определение. Вещественная квадратичная форма называетсяположительно определенной, если для любых изRⁿ > 0 иотрицательно определенной, если для любых изRⁿ < 0.

Если же для всех векторов изRⁿ неравенства являются нестрогими, т.е.  0 или  0, то квадратичная форма называется соответственно неотрицательно или неположительно определенной формой или полуопределенной. Определенные и полуопределенные квадратичные формы называются знакоопределенными.

Квадратичные формы, для которых не выполнено ни одно из этих условий, называются неопределенными квадратичными формами. Другими словами, квадратичная форма называется неопределенной, если при отличных от нуляквадратичная форма принимает как положительные, так и отрицательные значения.

Примеры. Квадратичная форма является положительно определенной, так как для любых > 0; квадратичная формаявляется неопределенной, так как знак правой части для может быть как положительным, так и отрицательным.

Поскольку каждую квадратичную форму можно записать в каноническом виде, то квадратичная форма будет положительно определенной; если все собственные числа матрицы, задающей квадратичную форму, будут положительными, и отрицательно определенной, если все собственные числа отрицательны. Ответ на вопрос об определенности квадратичной формы дает также и критерий Сильвестра. Для того чтобы квадратичная форма с симметрической матрицей была положительно определенной, необходимо и достаточно, чтобы главные миноры матрицы были положительными, т.е.

 ,  ,   ,...,  .

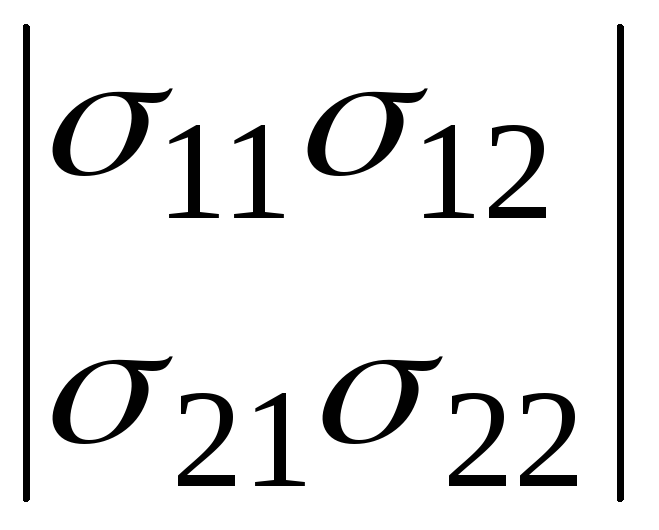
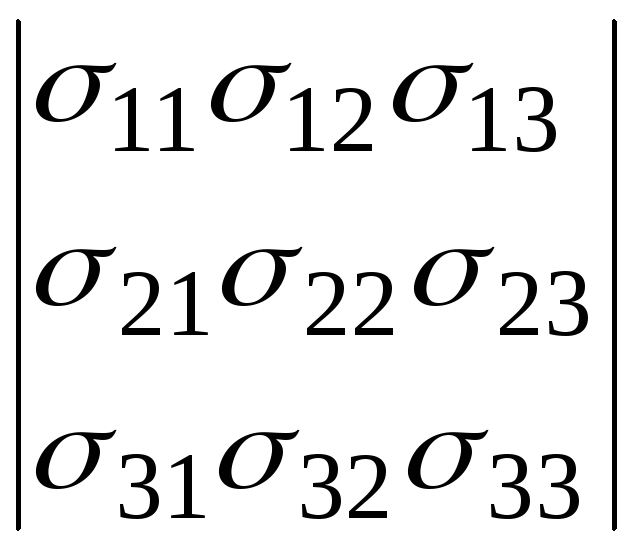
Из признака Сильвестра вытекает критерий отрицательно определенной формы.

Если , тои наоборот. Тогда, согласно критерию

Сильвестра, для имеем

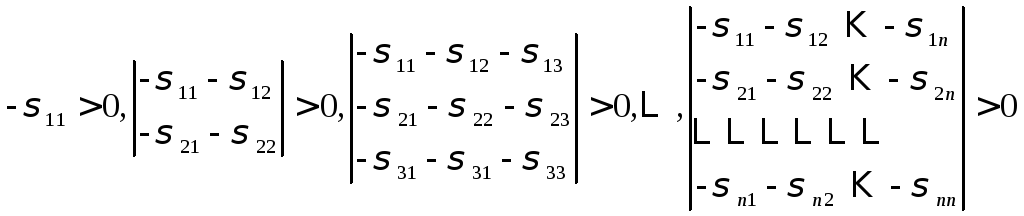
или

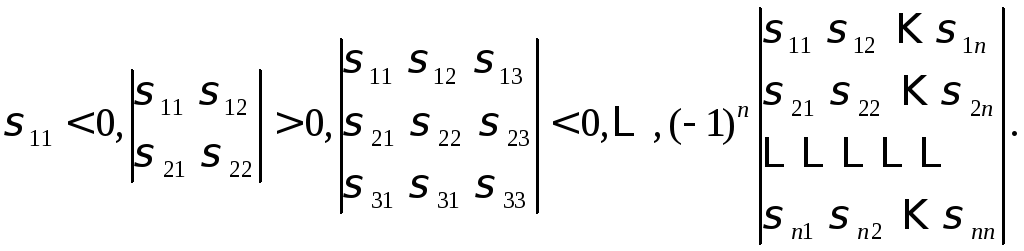
Таким образом, если знаки главных миноров квадратичной формы чередуются, то квадратичная форма отрицательно определена.

Упражнения

1. Найти собственные числа и собственные векторы линейного преобразования заданного матрицей

2. На примере матрицы показать, что характеристическими числами обратной матрицыА^–1 являются обратные значения характеристических чисел матрицы А.

3. Найти собственные числа и собственные векторы симметрической матрицы

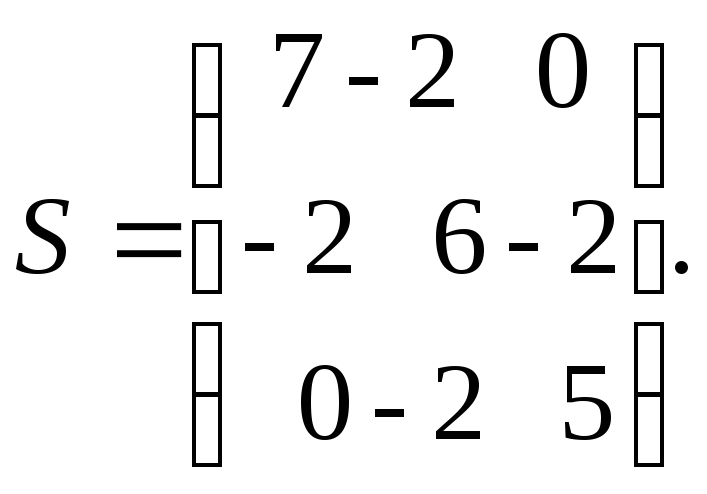
Показать, что собственные векторы ортогональны.

4. Даны матрицы

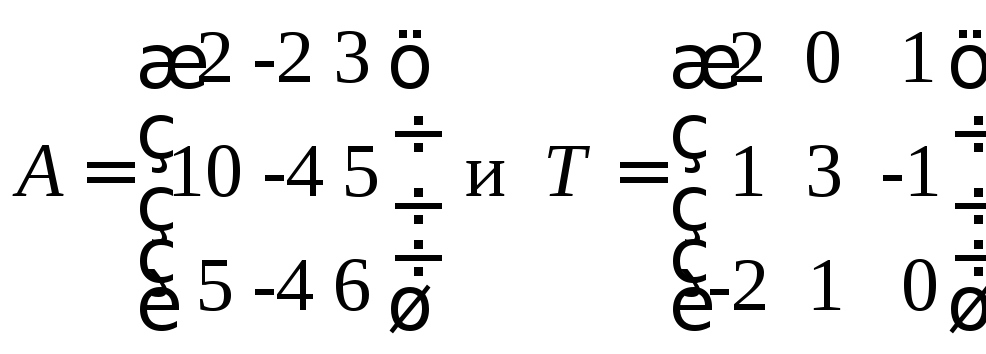
На примере матриц А и В = Т^–1АТ показать, что подобные матрицы имеют одинаковые характеристические числа.

5. Составить ортонормированный базис из собственных векторов матрицы:

а)

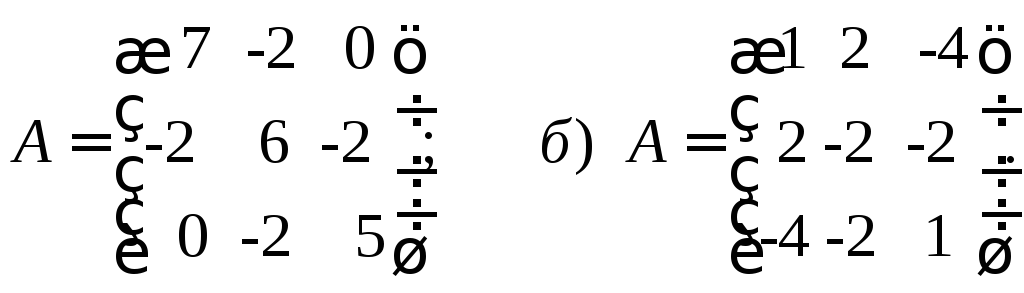
6. Привести к каноническому виду квадратичные формы и найти их собственные векторы, если

а)

б)

в)