1.1. Матрица перехода, связанная с преобразованием

системы координат в геометрическом пространстве

Матрицу перехода в геометрическом пространстве запишем для ортонормированных базисов. Выберем в качестве первого базиса и свяжем с ней систему координатx, y, z, а в качестве второго и связанную с ней систему координатx',y',z' (рис.2.8). Тогда

z' y'

z

x`

у

0

0 x

Рис. 2.8

,

, (8.1)

.

Если первую строку умножить последовательно на , учитывая, что

а

то получим: ;;.

Поступая аналогично со второй и третьей строками равенства, находим:

Таким образом, матрица перехода Т одного ортонормированного базиса к другому ортонормированному базису, связанная с преобразованием системы координат в геометрическом пространстве, имеет вид

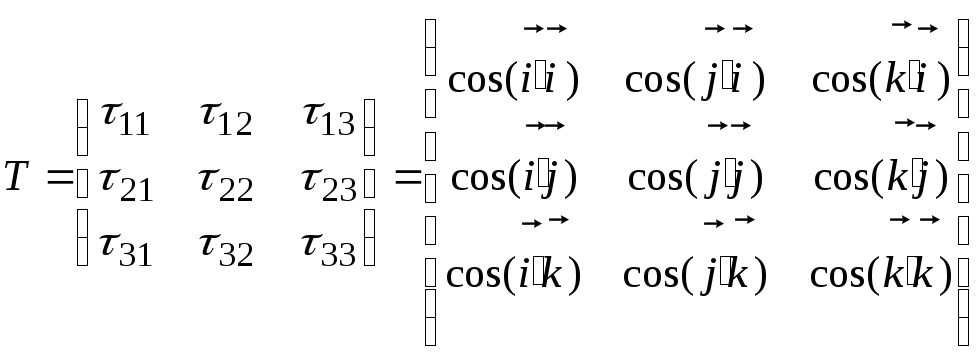(8.2)

и ее элементы определяются косинусами углов, которые образуются при повороте новой системы координат относительно старой. Если поворота системы координат при их преобразовании не происходит, а это наблюдается при параллельном переносе системы координат, тогда а остальные косинусы равны нулю. Поэтому матрица перехода для параллельного переноса системы координат является единичной

.

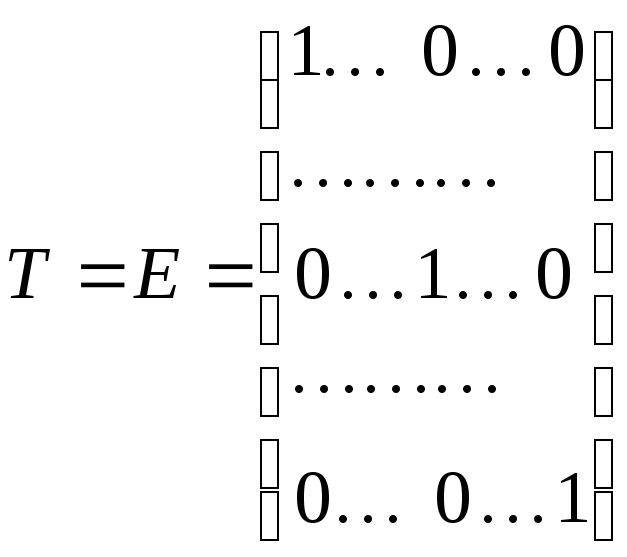Теперь рассмотрим матрицу перехода Т как матрицу линейного отображения пространстваR³ на себя. Пусть – радиус-вектор некоторой точкиМ в системе координат . В системе координатx, y, z этот же вектор имеет разложение:

где x₀, y₀, z₀ координаты начала координат в системе координатx, y, z. Тогда вектор , а

и они принадлежат пространству R³. Поэтому отображение в координатной форме имеет вид:

или(8.3)

Отсюда мы получаем формулу для изменения координат точки М при преобразовании системы координат в общем случае, когда происходит и параллельный перенос, и поворот системы координат.

или (8.4)

В формулах (8.3) и (8.4) предполагаются известным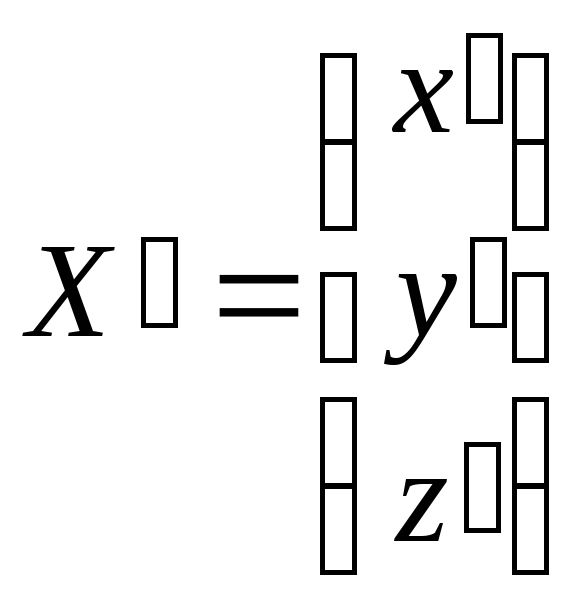и и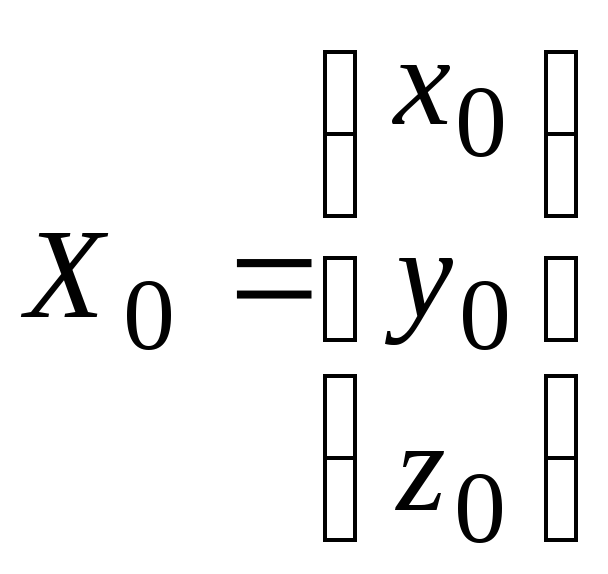, т.е. известны координаты точкиМ в новой системе координат и отыскиваются координаты точки в старой системе.

Более естественной является обратная задача, когда известны Х₀ и Х, а требуется найти . Для этого случая полагаеми тогда

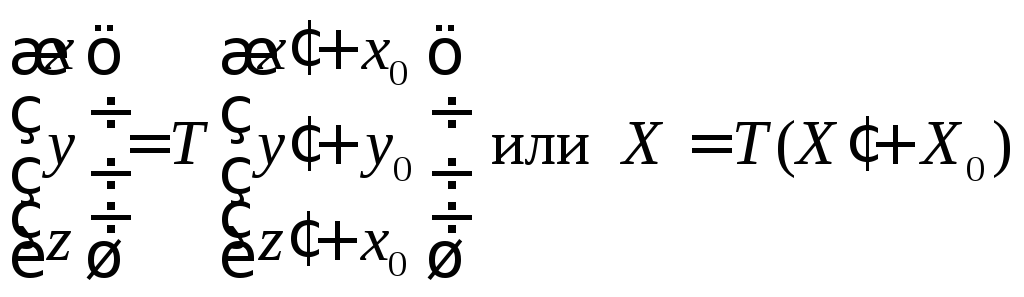
откуда

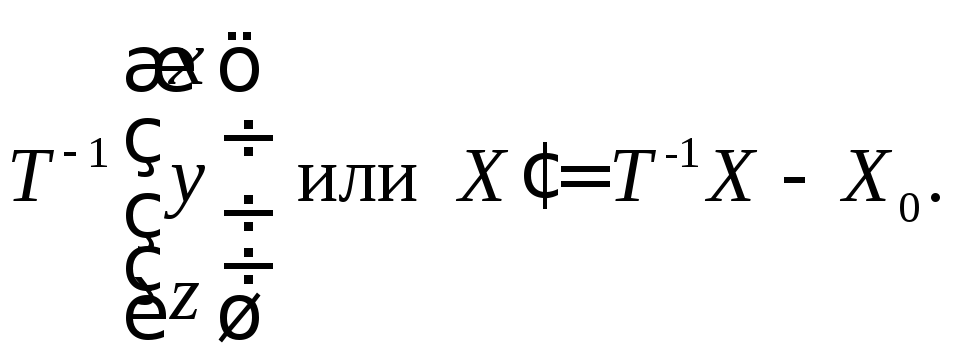(8.5)

1.2. Ортогональные матрицы перехода

Если мы все строки равенства (8.1) возведем в квадрат или перемножим между собой, то получим следующую систему равенств:

__  _  _  _ _ = _ , (8.6)

где _ – символ Кронекера,          

Следовательно, в матрице Т (8.2) сумма квадратов элементов, расположенных в каждом столбце (    равна 1, а сумма произведений соответствующих элементов двух любых различных столбцов (    равна нулю. Матрицы такого типа называются ортогональными.

Систему равенств (8.6), которая имеет место для элементов ортогональной матрицы Т можно переписать еще и в виде следующего условия Т^Т·T=E или T^T = T^–1, где T^T – транспонированная, а T^–1 – обратная матрицы к Т.

Затем, если естьj-й вектор-столбец в Т с компонентами , то соотношение (8.6) означает, что скалярное произведение,j = 1, 2, 3, i = 1, 2, 3 и, стало быть, вектор-столбцы ,j = 1, 2, 3 ортогональной матрицы Т образуют ортонормированный базис.

Данное определение ортогональных матриц распространяется не только на матрицы перехода третьего порядка п = 3, но и на матрицы порядка n > 3.

Определение. Квадратная матрица S = (_ij ), где i = 1, 2,..., n, j = 1, 2,..., n, для которой S^T·S = E (или  _1i _1j   _2i _2j  ......+ _ni_nj   _ij, где  _ij – символ Кронекера), называется ортогональной.

Из этого определения также следует, что для того, чтобы матрица была ортогональной, необходимо и достаточно, чтобы либо ее вектор-столбцы (либо вектор-строки) образовывали ортонормированный базис в Rⁿ.

Определитель D(S) ортогональной матрицы S равен +1 или –1. Действительно, так как определитель произведения матриц равен произведению определителей сомножителей, то

D(S·S^T) = D(S) · D(S^T) = [D(S)]² = D(E) = 1 и, следовательно, D(S) = 1. Значения +1 и –1 соответствуют различной ориентации вектор-столбцов, образующих базис. Так, если в качестве вектор-столбцов в S выбрать канонический ортонормированный базис ,........,, получимS = E и D(S) = +1. Если же мы возьмем ортонормированный базис ,.......,, то отвечающая ему ортогональная матрицаS´будет иметь определитель D(S´)= –1.