§5. Однородная система линейных уравнений

Система линейных уравнений называется однородной, если правые части этих уравнений равны нулю:

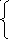a₁x₁ + a₁₂ x₂ + ... + a_1n x_n = 0,

a₂₁x₁ + a₂₂ x₂ + ... + a_2n x_n = 0,

...................................... (7.8)

a_k1x₁ + a_k2 x₂ + .... + a_kn x_n = 0.

Однородная система всегда совместна, так как расширенная матрица отличается от основной на столбец, представляющий нуль-вектор. Поскольку система, содержащая нуль-вектор, всегда линейно зависима, то ранг расширенной матрицы совпадает с рангом основной матрицы. Совместность однородной системы очевидна, так как она всегда имеет тривиальное решение х₁ = х₂ =.....= х_п = 0. Это решение будет единственным, если однородная система есть система Крамера, т.е. когда k = n и определитель D(A) основной матрицы A отличен от нуля. Другими словами, когда ранг r(A) основной матрицы равен числу n неизвестных системы: r(A) = n. Если же r(A) < n, то однородная система линейных уравнений имеет бесчисленное множество решений и совокупность решений системы образует векторное подпространство. Покажем это. Для этого запишем систему (7.8) в векторной форме в пространстве Rⁿ вектор-строк. В этом случае каждое уравнение системы представляет собой скалярное произведение двух векторов из Rⁿ: и :

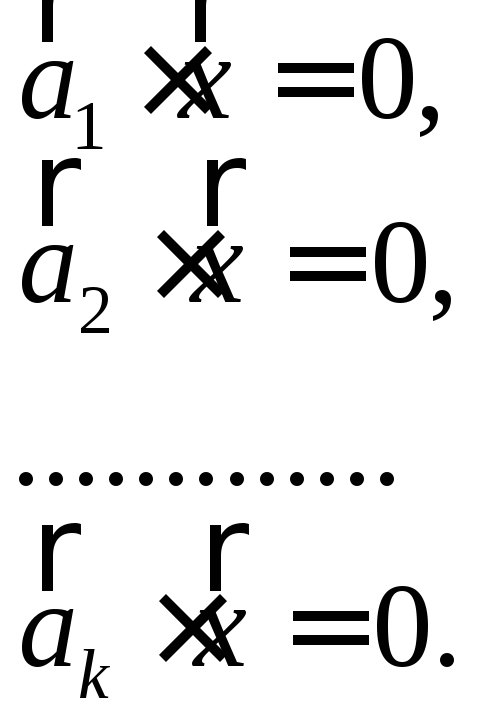
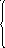
(7.9)

Докажем, что если вектора иесть решения системы (7.9), тоитакже будут решениями этой системы. Действительно, так как скалярное произведение дистрибутивно относительно сложения векторов и ассоциативно относительно умножения на число, имеем:

Отсюда следует, что иявляются также решениями однородной системы. Кроме этого, нейтральный (0,0,....,0) и симметричныйэлементы также принадлежат пространству решений. Таким образом, совокупность решений однородной системы образует векторное подпространство. Теперь определим размерность подпространства решений системы и построим его базис. Как мы уже сказали, подпространство решений содержит ненулевые вектора, еслиr(A) < n. Условие r(A) < n всегда выполнено, если число k уравнений системы меньше числа n неизвестных. Тот факт, что ранг основной матрицы A равен r(A), означает, что матрица A содержит минор порядка r, отличный от нуля; все же миноры более высоких порядков равны нулю, в том числе (если он существует) и минор порядка n. Не ограничивая общности, можно считать, что этим минором является главный минор матрицы A порядка r.

.

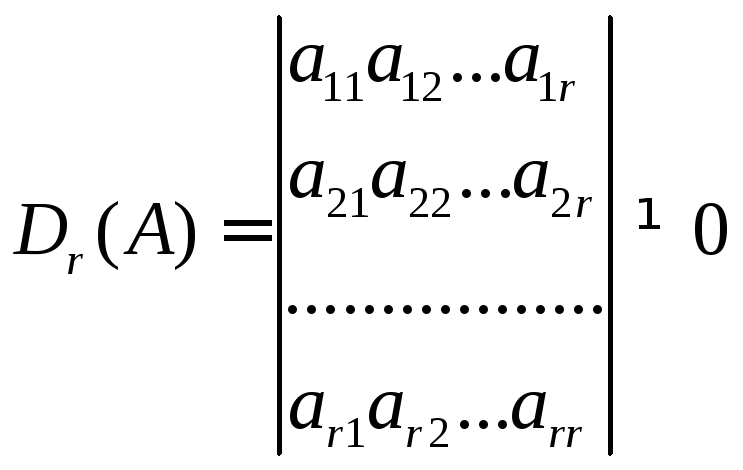Это всегда можно добиться, переставляя местами уравнения в системе. Тогда остальные к – r уравнений системы являются линейными комбинациями первых r уравнений системы и поэтому, не нарушая равносильности системы, эти уравнения из системы можно исключить. Оставшиеся же r уравнений системы запишем в следующем виде

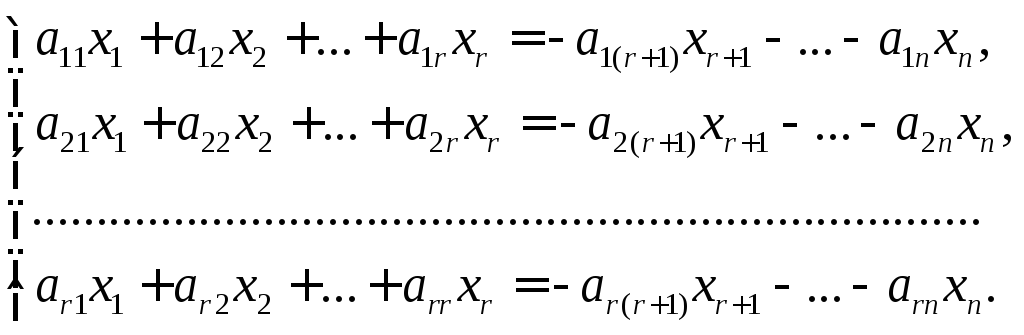(7.10)

Заметим, что если неизвестным x_r+1, . . ., х_n в системе (7.10) придать какие либо числовые значения, то получим систему Крамера, так как и, следовательно, остальные неизвестныех₁, х₂, . . ., х_r можно определить однозначно по правилу Крамера (7.7). Определим неизвестные х₁, х₂, . . ., х_r придавая для неизвестных х_r+1, х_r+2, . . ., х_n последовательно следующие значения (1,0,...,0), (0,1,0,...,0),. . . , (0,0,. . . , 1). Такой выбор обусловлен тем, что каждый набор из n – r чисел есть вектор канонического базиса пространства R^n-r. Положим, что для каждого указанного набора значений х_r+1, х_r+2, . . ., х_n для х₁, х₂, . . ., х_r получены соответственно следующие n – r наборов из r чисел . . .Ясно, что векторы

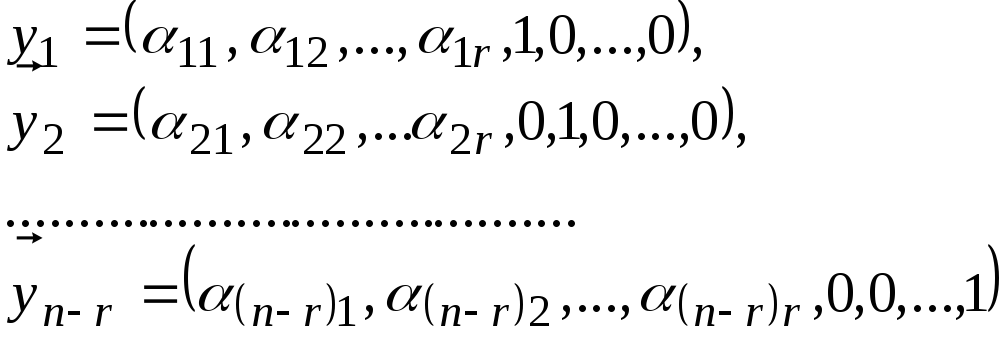(7.11)

являются решениями системы (7.10). Число координат у векторов равноn и они принадлежат пространству Rⁿ.

Докажем, что векторы линейно независимы. Действительно, если равенствозаписать в скалярной форме

,

используя компоненты (7.11), то оно выполняется лишь при условии _  _  _n-r = 0. Это непосредственно вытекает из уравнений, для которых j  r + 1. Нетрудно показать также то, что любое решение однородной системы (7.10) является линейной комбинацией векторовс  коэффициентамит.е.

, (7.12)

где могут принимать любые значения изR. Для доказательства этого при решении системы (7.10) для неизвестных x_r+1,...,x_n полагаем значения (_r+1, 0,..., 0), (0, _r+2, 0,…,0),.....,(0,0,...,_n).

Таким образом, векторы с компонентами (7.11) образуют базис подпространства решений однородной системы (7.8) размерностиn – r. Выражение (7.12), определяющее все множество решений подпространства, называется общими решениями однородной системы. Совокупность линейно независимых решений системы называетсяфундаментальной системой решений. Переменные x_r+1,...,x_n называются свободными, x₁,...,x_r – базисными.

Замечание. Построение фундаментальных решений, проведенное нами выше, не является обязательным и при решении конкретных задач выбор значений x_r+1,...,x_n может быть другим.

Пример. Пусть дана однородная система уравнений

x₁ + 2x₂ – 5x₃ + 3x₄ = 0,

2x₁ + 5x₂ – 6x₃ – x₄ = 0,

5x₁ + 12x₂ – 17x₃ + x₄ = 0,

в которой число неизвестных n = 4, а число уравнений к = 3. Поскольку к  n то r(A)  n и, следовательно, система имеет бесчисленное множество решений. Для построения фундаментальных и общего решений системы определим ранг r(A) основной матрицы

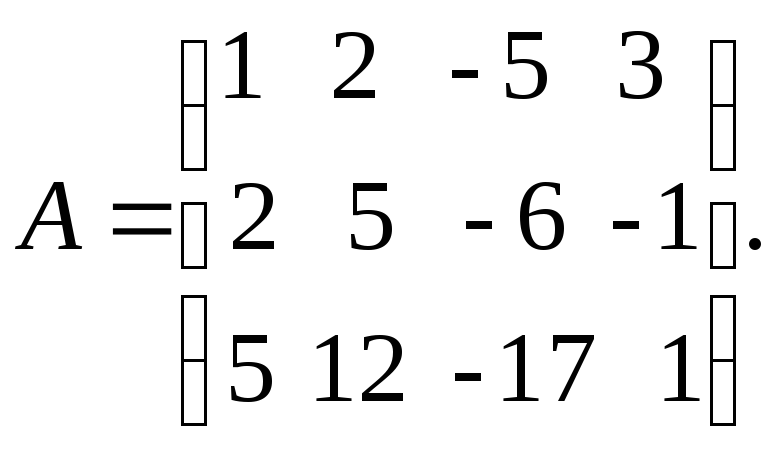
Рассмотрим главные миноры: Для матрицыА существует еще один минор третьего порядка но он также равен нулю. Таким образом, все миноры третьего порядка матрицыА, равны нулю, а среди миноров второго порядка есть минор отличный от нуля. Следовательно, ранг r(A) матрицы А равен 2. Это означает также, что третье уравнение системы есть линейная комбинация первых двух и его из системы можно исключить. Действительно, третье уравнение получается, если второе уравнение умножить на 2 и сложить с первым. После исключения из системы третьего уравнения, оставшиеся два уравнения, перепишем в следующем виде

х₁ + 2х₂ = 5х₃ – 3х₄,

2х₁ + 5х₂ = 6х₃ + х₄.

Полагая х₃ = 1, а х₄ = 0, получим фундаментальное решение системы

х₁ + 2х₂ = 5,

2х₁ + 5х₂ = 6  х₁ = 13, х₂ = – 4, = (13, – 4, 1, 0).

Полагая х₃ = 0, а х₄ = 1, определим

х₁ + 2х₂ = –3,

2х₁ + 5х₂ = 1  х₁ = –17, х₂ = 7, = (–17, 7, 0, 1).

Общее решение системы

где любые числа изR.

Итак, решения системы составляют векторное подпространство размерности n – r = 4 – 2 = 2.