Из подобия треугольников авс и ав'с' следует (как в случае   , так и в случае   ), что.

Но , следовательно.

Из доказательства свойства 4 вытекает следующее условие компланарности векторов. Для того чтобы три вектора ,ибыли компланарны, необходимо и достаточно, чтобы они удовлетворяли соотношению, гдеR и R. Это соотношение читается так: вектор естьлинейная комбинация векторов и.

Таким образом, множество свободных векторов, на котором заданы данные операции сложения векторов и умножение вектора на число из R, образует векторное пространство над полем R.

Теперь рассмотрим, как можно задать вектора с помощью декартовой прямоугольной системой координат, и установим их соответствие с векторами из пространства R³.

3.3. Задание свободных векторов при помощи декартовой системы координат и соответствие их с векторами из векторного пространства r3

Выберем в пространстве декартовую прямоугольную систему координат x, y, z. Рассмотрим произвольный вектор , который задан направленным отрезкомНапомним, что точкаА может быть любой точкой пространства. В выбранной системе координат определим координаты начала вектора – точки А и конца этого вектора – точки В (рис.2.4).

Пусть координатами точки А является тройка чисел (х₁, у₁, z₁), а точки В – (х₂, у₂, z₂). Тогда координатами вектора называют упорядоченную тройку чисел (х, у, z), вычисляемые по формулам:

х = х₂ – х₁; у = у₂ – у₁; z = z₂ – z₁, (рис.2.4)

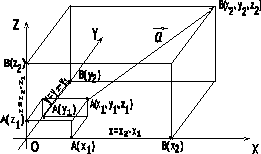
Рис. 2.4

Записывают это таким образом (х, у, z) или (а_х, а_у, а_z).

Если начало направленного отрезка совпадает с началом координатА(х₁, у₁, z₁) = О (0, 0, 0,), то направленный отрезок называется радиус-вектором точки В. В этом случае координаты (х, у, z), вектора совпадают с координатамих₂, у₂, z₂ точки В: х = х₂, у = у₂, z = z₂.

Таким образом, выбрав в пространстве декартову систему координат, мы с ее помощью можем установить соответствие между любым вектором , заданным направленным отрезкоми векторомиз векторного пространстваR³, координаты которого определяются упорядоченной тройкой чисел (х, у, z). Если указанное соответствие, представляющее собой способ нахождения координат методом проектирования, обозначить через f, то

f : =f () = (х, у, z).

Покажем, что f является взаимно однозначным отображением. Для этого рассмотрим теорему о равенстве векторов.

Теорема. Два вектора равны тогда и только тогда, когда равны их координаты.

Для доказательства этой теоремы вначале покажем, как можно задать вектор при помощи его длины и углов, которые он образует с координатными осями.

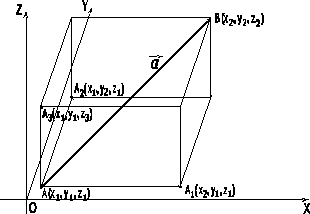
Рассмотрим произвольный направленный отрезок , принадлежащий множеству вектора. Построим на, как на диагонали, прямоугольный параллелепипед (рис.2.5) со сторонамиАА₁ = х = х₂ – х₁ = а_х; АА₂ = у = у₂ – у₁ = а_у; АА₃ = z = z₂ – z₁ = а_z .



_



Рис. 2.5.

Заметим, что все точки, лежащие на плоскости, параллельной какой-либо координатной плоскости, имеют равные координаты той оси, к которой эта плоскость перпендикулярна. Если точки расположены на прямой, параллельной какой-либо из координатных осей, то для этих точек изменяется только координата той оси, которой эта прямая параллельна. Две другие координаты одинаковы. Например, точки А и А₁ (рис.2.5) лежат на прямой, параллельной оси Ох, следовательно, для этих точек изменяется только координата х.

Теперь обозначим через ,  и  углы, которые образует направленный отрезок с осями координатx, y, z соответственно или со сторонами параллелепипеда АА₁, АА₂, АА₃ (рис.2.5). Из прямоугольных треугольников АА₁В, АА₂В и АА₃В находим

х = х₂ – х₁ = а_х = cos,

у = у₂ – у₂ =а_у =  cos, ( 4.2 )

z = z₂ – z₁ = a_z =  cos,

где  =  =,

cos, cos и cos называются направляющими косинусами, и для них имеет место соотношение

cos² + cos² + cos² = 1. ( 4.3)

Теперь на основании полученных формул докажем теорему равенства векторов. Рассмотрим два вектора ис координатами соответственноx₁,y₁,z₁ и x₂,y₂,z₂.

Необходимость. Покажем, что если векторы равны (=), то и их координаты тоже равны (x₁ = x₂; y₁ = y₂; z₁ = z₂). Из равенства векторов следует, что  = , а также, что cos_  cos_, cos_ = cos_, cos_ = cos_, так как векторы коллинеарны и одинаково направлены. Если бы векторы были коллинеарны и противоположно направлены, то cos_  – cos_, cos_ = – cos_, cos_ = – cos_. Теперь из формул (4.2) следует:

x₁ = cos_ =  cos_ = х₂,

у₁ = cos_ =  cos_ = у₂,

z₁ = cos_ =  cos_ = z₂,

что и требовалось доказать.

Достаточность. Так как координаты векторов иравны, то

=  и cos_ = cos_, cos_ = cos_, cos_ = cos_.

Второе условие означает, что векторы иколлинеарны и направлены в одну сторону, а с учетом =  такие вектора считаются равными, т.е. =.

. Из теоремы равенства векторов непосредственно следует, что отображение = (x,y,z) является взаимно однозначным. Действительно, каждому вектору из векторного пространства свободных векторов можно поставить в соответствие единственный вектор= (x,y,z) из векторного пространства R³ и наоборот, каждой упорядоченной тройке чисел (x,y,z), т.е. вектору из R³ , можно поставить в соответствие единственный вектор из векторного пространства свободных векторов. Для построения этого вектора достаточно построить радиус-вектор точкиВ(x,y,z) в выбранной системе координат. Тогда множество всех направленных отрезков, равных направленному отрезку и является векторомс координатамиx,y,z. Отметим, что это соответствие зависит от выбора системы координат.

Если вектор расположен в одной из координатных плоскостей, то одна из координат равна нулю, например, если эта плоскостьхОу, то координата z = 0. Изображать такой вектор можно направленным отрезком, лежащим в любой из плоскостей, параллельной плоскости хОу. В этом случае каждому вектору , расположенному в координатной плоскости, можно поставить в соответствие упорядоченную пару чисел (х,у), представляющую собой вектор из векторного пространства R² и это соответствие взаимно однозначно.

Если вектор расположен на одной из координатных осей, то остальные две его координаты равны нулю и поэтому каждому вектору, расположенному на координатной оси, можно поставить в соответствие вектор с координатойх из векторного пространства R¹ и это соответствие взаимно однозначно. Изображать такой вектор можно направленным отрезком, расположенным на любой прямой, параллельной соответствующей координатной оси.

Покажем теперь, что операции сложения свободных векторов и умножение их на число из поля R находятся в полном соответствии с аналогичными операциями над векторами из R³, т.е. относительно данных операций эти пространства изоморфны. Перечислим эти операции без доказательства, так как все они доказаны в курсе средней школы.

Сумма свободных векторов. Координаты суммы двух свободных векторов равны суммам соответствующих координат слагаемых.

На координатной оси: (х₁) и (х₂);

(х₁) + (х₂) = (х₁ + х₂).

На координатной плоскости : (х₁,у₁) и (х₂,у₂);

(х₁,у₁) + (х₂,у₂) = (х₁ + х₂, у₁ + у₂).

В пространстве: (х₁,у₁,z₁) и (х₂,у₂,z₂);

(х₁,у₁,z₁) + (х₂,у₂,z₂) = (х₁ + х₂, у₁ + у₂, z₁ + z₂) – соответствие см. формулу (4.1).

Умножение свободного вектора на число из поля R. Координаты произведения вектора(x,y,z) на число  равны произведениям этого числа на соответствующие координаты вектора .

) – соответствие см. формулу (4.1).

Следствие. Для того чтобы два вектора (х₁,у₁,z₁) и (х₂,у₂,z₂) были коллинеарны, т.е. , необходимо и достаточно, чтобы соответствующие координаты векторов были пропорциональны:.

Кроме этих двух операций введем еще одну операцию над свободными векторами, с которой вы познакомились в курсе средней школы, но смысл, которой мы раскроем чуть позже.