§2. Комплексно сопряженные числа

Поскольку (–i )² = –1, то число –i обладает свойством числа i, а именно, его квадрат равен –1.

Определение. Комплексно сопряженным с числом z = а + iв называется комплексное число = а – iв, т.е. число, отличающееся от z только знаком мнимой части.

Отображение z  есть взаимно однозначное отображение множества комплексных чисел на себя, т.е.перестановка этого множества, так как если z = а + iв, z' = а' + iв^', то условие = ' влечет а = а' и в = в', и, следовательно, z = z'.

Пусть z = а + iв и z' = а' + iв'; имеем

( z + z' ) = (а +а' ) – i (в +в' ) = + ' .

Точно такжеz·z' = (аа' – вв') – i (ав' + а'в) = ·'.

Итак, отображение z  есть изоморфизм относительно сложения и умножения.

Имеют место, также, следующие свойства:

1. z + = 2Re z = 2а. Следовательно, сумма комплексного числа с его сопряженным всегда есть действительное число;

2. z – = 2i Im z = 2iв, следовательно, разность комплексного числа с его сопряженным всегда есть мнимое число;

3. z·= а² + в². Следовательно, произведение комплексного числа на его сопряженное есть действительное число, которое  0;

4. если z = , то z – действительное число.

Рассмотрим уравнение ах² + вх + с = 0, где аR, вR, и сR . (2.3)

Решениями такого уравнения являются числа:

и .

Если дискриминант D = в² – 4ас > 0, то решениями уравнения (2.3) будут два различных действительных числа. При условии D = 0 и также принадлежат R. Для случая же D  0 уравнение (2.3) в поле R решений не имеет. Определим их в поле С комплексных чисел. С этой целью преобразуем дискриминант D = в² – 4ас = – (4ас – в²) = i²(4ac – в²), где 4ас – в²  0, тогда имеем:

и ;

Следовательно, уравнение (2.3) у которого D  0, на поле С имеет два корня: комплексное число х =  + i и комплексно сопряженное ему

= – i.

§3. Модуль комплексного числа. Деление двух комплексных чисел

Определение. Модулем комплексного числа z называется и обозначается |z| отображение z  |z| множества С во множество неотрицательных чисел из R, определяемое как z| =.

Модуль является абсолютным значением. Действительно:

1. |z|  0, а |z| = 0 влечет z = 0 и наоборот.

2. | z₁z₂ | = |z₁|| z₂|. В самом деле,

| z₁ z₂ |²=(z₁ z₂ ) (z₁ z₂) = z₁  z₂  == |z₁|² | z₂|².

3. |z₁+ z₂|  |z₁|+| z₂|.

Кроме этих трех свойств добавляется еще одно:

4. |z | = ||.

Введение модуля позволяет сразу записать действительную и мнимую части для частного двух комплексных чисел z₁ и z₂.

(2.4)

§4. Геометрическая интерпретация комплексных чисел

Геометрически комплексное число z = a + iв, как элемент множества R×R, представляется точкой М на координатной плоскости xOy с координатами (а,в). И это отображение, как мы видели (книга 1, гл.2, §4, п.4.2), взаимно однозначно.

Рассмотрим отрезок ОМ и угол , который он составляет с осью Оx (рис.2.1). Определим длину отрезка ОМ. Из прямоугольного треугольника ОММ₁ по теореме Пифагора

,

следовательно, длина отрезка ОМ соответствует модулю комплексного числа z: d(ОМ) = |z|.

y

М₂ М(а,в) z

в

0 φ М₁

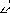-а -φ а х

-в

М(-а,-в)  -z М(а,-в) 

Рис. 2.1

Угол  при заданном d(ОМ) однозначно определяет положение точки на координатной плоскости, а, следовательно, и комплексное число. Этот угол называют аргументом комплексного числа и обозначают Arg z. Аргумент комплексного числа считается положительным, если он отсчитывается от положительного направления оси Оx против часовой стрелки, и отрицательным при противоположном направлении отсчета. Очевидно, что аргумент  для заданного комплексного числа определяется не однозначно, а с точностью до слагаемого, кратного 2π, т.е.

φ = Arg z = argz + 2πm, где m = 0,      

arg z – значения аргумента комплексного числа, определяемые неравенствами 0  arg z  2π (или –  arg z  ) и которые называют главными значениями аргумента комплексного числа.

Если –arg z < и точка М находится в координатной полуплоскости положительных значений оси Оx (а > 0), то arg z = arc tg, если же отрицательных значений (а < 0), то arg z   + arc tg.При а  0: arg z  , если b > 0, и arg z  –, если b < 0. Для определения arg z можно пользоваться также следующей системой уравнений

cos =, sinφ =.

Откуда, при условии, что 0  < 2π

Таким образом, под Аrg z понимается все множество углов, отвечающих числу z и, как видно из рис.2.1, имеем: Аrg= –Аrg z; Аrg(–) = π + Аrg z.

Множество действительных чисел характеризуется условием (а,0) и, следовательно, они лежат на оси Оx. Множество же мнимых чисел условием (0,в) и лежат на оси Oy. Поэтому ось Ox называется действительной, а ось Oy – мнимой осью. Вся плоскость в целом называется комплексной плоскостью.