§2. Алгебраичесие операции над матрицами.

ВЕКТОРНОЕ ПРОСТРАНСТВО МАТРИЦ

Поскольку матрица ассоциирована с системой векторов, а операции сравнения и сложения вводятся только для векторов, принадлежащих единому пространству, поэтому сравнивать и складывать можно только матрицы одинаковых размеров.

Равенство. Две матрицы одинаковых размеров, соответствующие элементы которых равны между собой, называются равными.

Сложение. Суммой двух матриц А и В одинаковых размеров, называется матрица С того же размера, элементы которой равны суммам соответствующих элементов слагаемых матриц.

= (a_ij), = (в_ij),

С= А + В =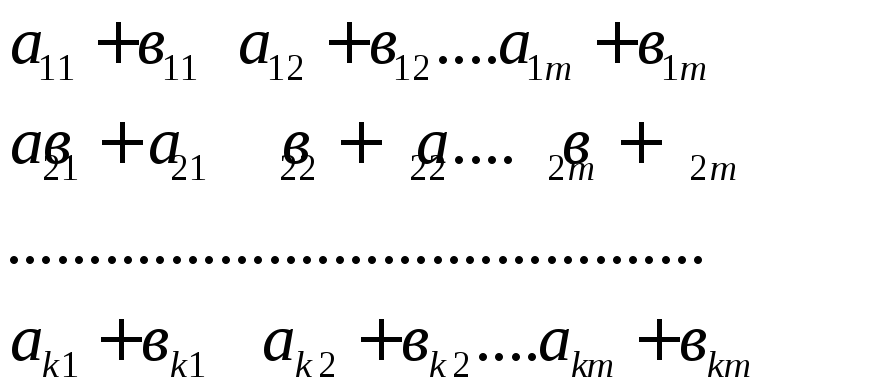, (с_ij ) = (a_ij + в_ij),

где i = 1,2,....,k; j = 1,2,...,m.

Сложение ассоциативно и коммутативно, поскольку это имеет место для сложения a_ij + в_ij в Р; имеется нейтральный элемент – нулевая матрица, обозначается О или (0), у которой все элементы нули, и , каково бы ни было. Каждая матрицаА из элементов a_ij имеет противоположную (симметричную), обозначаемую –А, у которой все элементы суть – a_ij и А + (–А) = О. Таким образом, операция сложения на множестве матриц одинаковых размеров образует абелеву группу.

Умножение матрицы на число из Р. Произведением матрицы на число (или числа на матрицу) называется матрица, элементы которой есть произведения элементов данной матрицы на это число:

    a_ij ) = (a_ij )= ,

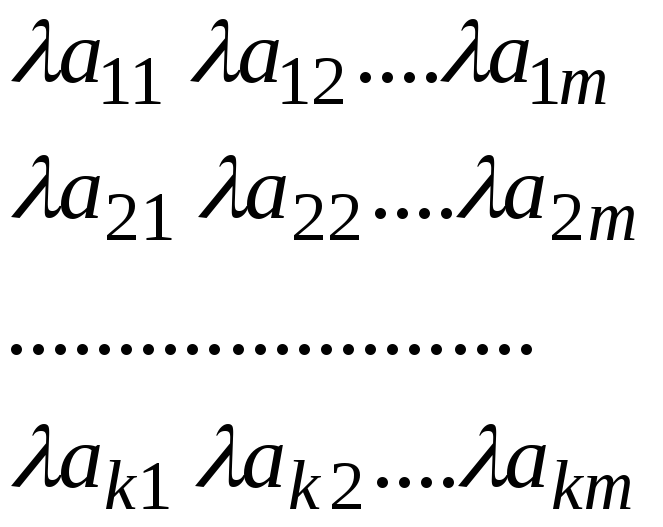где i = 1,2,...,k; j = 1,2,...,m.

Видно, что умножение на число коммутативно и полученная матрица имеет ту же размерность, что и умножаемая матрица. Кроме этого:

А+В) =  А+В, ибо (а_ij+в_ij ) =  а_ij+ в_ij ;

(+ А =  А+А, ибо (+) а_ij =  а_ij+ а_ij ;

 А) = (  А, ибо  а_ij ) = (  а_ij ;

 А = А, ибо  а_ij = а_ij, где  = 1 Р – нейтральный элемент умножения в Р, каковы бы ни были матрицы А и В из k строк и m столбцов и каковы бы ни были   Р и   Р.

Таким образом, множество матриц А, состоящих из k строк и m столбцов, образует векторное пространство над полем Р.

Обозначим через _ij матрицу из k строк и m столбцов, у которой все элементы нули, кроме элемента i-строки и j-того столбца – равного  = 1; т.е. положим

_ij = i.

j

Количество таких матриц равно числу элементов в матрице, т.е. произведению k·m.

Тогда любая матрица А = (_ij) состоящих из k строк и m столбцов имеет вид

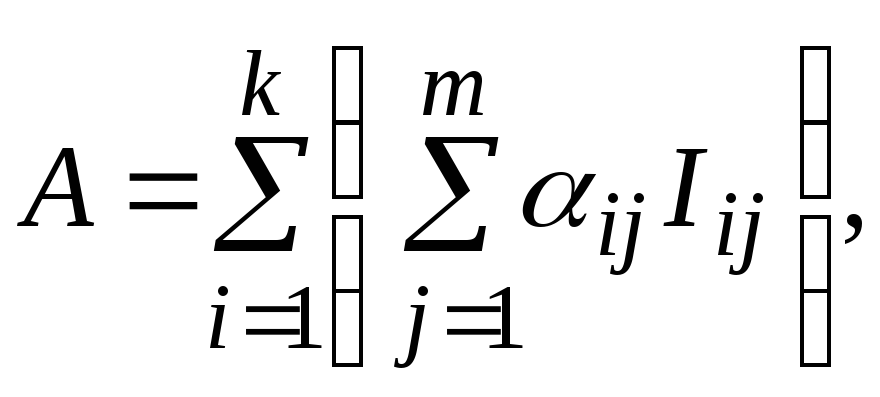
и это представление единственно. Следовательно, матрицы _ij составляют базис векторного пространства матриц из k строк и m столбцов, и значит, это векторное пространство имеет конечную размерность, равную произведению k·m, что составляет общее число элементов в матрице.

Умножение двух матриц. Произведением двух матриц А, размером m×k и В, размером k×n, называется матрица С, размером m×n, у которой элемент с_ij равен сумме произведений элементов i-той строки матрицы А на соответствующие элементы j-столбца матрицы В.

Пусть даны матрицы

и,

тогда их произведение

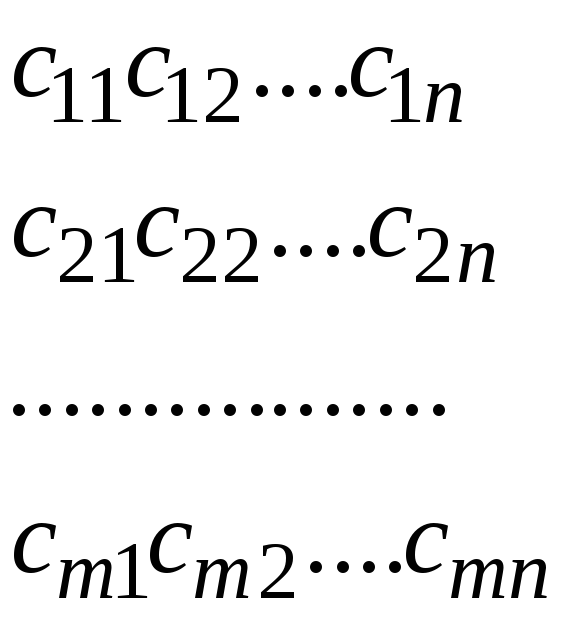С= А·В ==(c_ij ),

где c_ij = а_i1 в_1j + а_i2 в_2j + . . . + а_ik в_kj = i = 1,2,..., m, j = 1,2, . . ., n.

Замечание. Две матрицы А и В, взятые в определенном порядке можно перемножать только в случае если число столбцов первой матрицы равно числу строк второй матрицы, т.е. они имеют размеры mk и kn. Такие матрицы называются согласованными.

Для умножения матриц справедливы следующие свойства:

1. Произведение любой матрицы на согласованную с ней нуль матрицу равно нуль матрице.

2. Произведение матриц не коммутативно, т.е. в общем случае А·В  В·А.

При этом предполагается, что А·В и В·А имеют смысл. Если А·В = В·А, то матрицы называются коммутирующими (перестановочными).

3. Пусть А, В и С матрицы, которые можно складывать или перемножать, а  – некоторое число из Р. Тогда

(А·В)·С = А·(В·С)

(АВ) = (А)В = А(В)

А(В+С) = АВ+АС.