§2. Изменение матрицы линейного отображения при замене базисов

Рассмотрим линейное отображение f n-мерного пространства K над полем P в m-мерное пространство F над полем P и пусть, если в пространстве K задан базис , а в пространствеF базис , то отображениеf ассоциировано с матрицей А, представляющей линейное отображение пространстваPⁿ в P^m, Перейдем в этих пространствах к другим базисам, соответственнои, которые связаны с первоначальными базисами матрицами переходаи. Наша задача определить, какой вид примет матрицаА в базисах и. Обозначим эту преобразованную матрицуВ.

Рассмотрим произвольный векториз пространстваPⁿ, и его образ из пространстваP^m в базисах и. При замене базисов пространстваPⁿ и P^m отображаются каждое само на себя посредством матриц перехода S и T. При этом вектора ибудут прообразами векторов соответственнои. Тогда матрица В задается при помощи соотношений и, значит,B = T^–1AS. Это и есть искомая формула для установления взаимосвязи между матрицами А и В, представляющих одно и тоже линейное отображение f пространства К в пространство F, при замене в них базисов, определяемое матрицами перехода S и Т.

Если F = K, причем первоначальные, а также новые базисы в пространствах K и F совпадают, то А и S = Т будут квадратными матрицами одного порядка. Тогда получим В = T^–1АТ; В называется матрицей, преобразованной из А посредством Т; матрицы В и А называются подобными. Если А обратима, то T^–1 (А^–1)Т = (T^–1АТ)^–1 = В^–1.

Теперь попытаемся найти в К такой конкретный базис, относительно которого связанная с f квадратная матрица, определяющая отображение Pⁿ в Pⁿ имела бы наиболее простую форму.

2.1. Собственные значения, собственные векторы

квадратной матрицы

Легко показать, что равенство В = T^–1АТ влечет равенство определителей: D(B) = D(A). Действительно, из правила умножения определителей имеем

D(B) = D(T^–1)·D(A)·D(T) = D(A)D(E) = D(A)·1 = D(A).

С другой стороны, матрица, преобразованная из единичной, сама является единичной: T^–1ЕТ = Е; следовательно, для любого   , имеем

В – Е = T^–1 (А – Е)Т,

и значит, определитель D(А – Е) зависит только от линейного отображения f и не зависит от выбора конкретного базиса в К.

Если ,

то 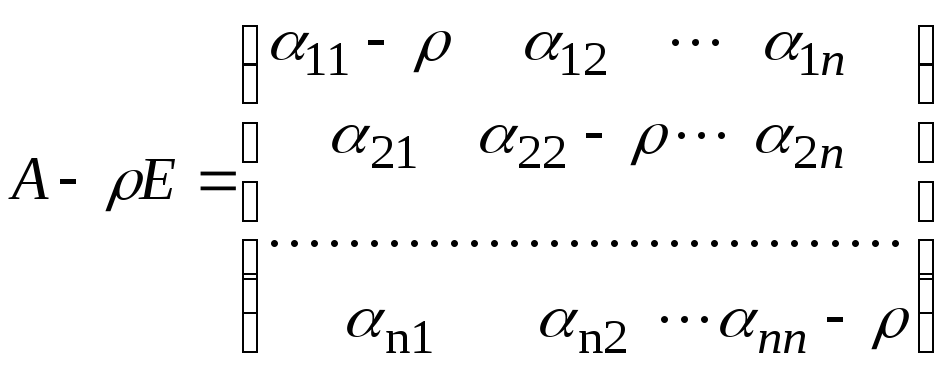и

D(A–   ⁿ ⁿ + q_n-1 ^n-1 + q_n-2 ^n-2 + . . . + q₁  D(A), есть многочлен от  степени, в точности равной n. Записывать, чему равны коэффициенты q_i, нам нет необходимости.

Определение 1. Многочлен D(A–  называется характеристическим многочленом отображения f.

Его коэффициенты зависят только от линейного отображения f и не зависят от выбора базиса в К. То же самое будет относиться к нулям этого многочлена и к их кратности.

Определение 2. Собственными значениями или характеристическими числами отображения f называются нули характеристического многочлена D(A– , т.е. корни уравнения D(A–  = 0 – это уравнение называется характеристическим.

Если Р есть поле С комплексных чисел, то многочлен степени n имеет точно n нулей, принадлежащих С; если считать каждый нуль столько раз, какова его кратность (основная теорема алгебры). Поэтому отныне мы будем предполагать, что Р есть поле С.

Пусть ₁ есть собственное значение, а значит такое действительное или комплексное число, что D(A–₁  = 0. Тогда матрица A–₁ необратима, и существует, по крайней мере, один такой ненулевой вектор , что. Обратно, если существует такой ненулевой вектор, что, то рассуждением, обратным к приведенному, убеждаемся, что₁ есть собственное значение.

Определение 3. Вектор называетсясобственным вектором матрицы А, принадлежащим собственному значению ₁, если , с

Если есть вектор изК, отвечающий вектору , то, что показывает, чтои₁ зависят только от f.

Вектор называетсясобственным вектором линейного отображения f.

Перечислим некоторые свойства собственных векторов и собственных значений матрицы А, которые являются также и свойствами собственных векторов и собственных значений линейного отображения f.

1. Каждому собственному вектору соответствует единственное собственное число.

2. Если – собственный вектор матрицыА с собственным числом , то любой вектор коллинеарный вектору, также является собственным вектором матрицыА с тем же самым числом .

3. Если и собственные векторы матрицыА с одним и тем же собственным числом , то их сумма + также является собственным вектором матрицыА с тем же самым числом .

Из свойств 2 и 3 следует, что каждому собственному числу соответствует бесчисленное множество (коллинеарных) собственных векторов. Это множество вместе с нулевым вектором, который всегда является собственным вектором, образует подпространство пространства Сⁿ, если речь идет о собственных векторах матрицы и пространстваК, если речь идет о собственных векторах линейного отображенияf.

4. Если собственные векторы (либо) принадлежат различным собственным значениям, то они линейно независимы.

Последний пункт позволяет решить вопрос о приведении квадратной матрицы к более простой форме.