§2. Метод гаусса

Над системой (7.1) линейных уравнений можно производить следующие операции, которые не нарушают равносильности системы уравнений:

а) прибавлять к обеим частям уравнения соответствующих частей другого уравнения, умноженных на некоторое число;

б) переставлять уравнения в системе;

в) исключать из системы уравнения 0х₁ + 0х₂ + . . . + 0х_n = 0. Поскольку это равенство является тождеством, и ему удовлетворяют любые значения х₁, х₂,. . . , х_n .

С помощью этих операций любую систему линейных уравнений можно привести к треугольному

с₁₁х₁ + с₁₂х₂ + . . . + с_1rх_n + . . . + с_1nх_n = d₁,

с₂₂х₂ + . . . + с_2rх_r + . . . + с_2nx_n = d₂, (7.2)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

с_rrх_r + . . . + с_rnх_n = d_r,

. . . . . . . . . . . . . . . . . .

+ с_nnx_n = d_n

или трапецеидальному виду

с₁₁х₁ + с₁₂х₂ + . . . + с_1rх_n + . . . + с_1nх_n = d₁,

с₂₂х₂ + . . . + с_2rх_r + . . . + с_2nx_n = d₂, (7.3)

. . . . . . . . . . . . . . . . . . . . . . . . . . .

с_rrх_r + . . . + с_rnх_n = d_r.

При приведении системы к треугольному или трапецеидальному виду могут возникать уравнения 0х_i + 0х_i+1 + . . . + 0х_n = d_i, i = 1,2, . . .,n. Если d_i = 0, то эти уравнения являются тождествами и из системы исключаются, если же d_i  0, то этому уравнению не удовлетворяют никакие значения х_j . В этом случае система не имеет решений, она несовместна.

Совместная система уравнений, приведенная к треугольному виду (7.2) имеет единственное решение и, следовательно, является определенной. Если же совместная система приведена к трапецеидальному виду (7.3), причем r  n, то, придавая x_r+1, x_r+2, . . . , x_n произвольные значения, мы можем из системы (7.3) определить х₁, х₂,. . . , х_r и построить решение системы. Однако, учитывая, что x_r+1, x_r+2, . . . , x_n могут принимать любые значения из R, мы получаем неопределенную систему, и число ее решений бесконечное множество. Неизвестные, которые принимают произвольные значения, называются свободными, вспомогательными, независимыми и их количество равно n – r.

Примеры. 1. Решить методом Гаусса систему

4х₁ + 2х₂ + х₃ = 4,

х₁ + 3х₂ + 2х₃ = 2,

2х₁ – х₂ + х₃ = 5.

Исключим из 2-го и 3-го уравнений данной системы неизвестное х₁. Для этого второе уравнение умножим на –4, а третье на –2 и сложим с первым:

4х₁ + 2х₂ + х₃ = 4,

–10х₂ –7х₃ = –4,

4х₂ – х₃ = –6.

Теперь умножим третье уравнение полученной системы на 5/2 и прибавим к нему второе уравнение:

4х₁ + 2х₂ + х₃ = 4,

–10х₂ – 7х₃ = –4,

х₃ = –19.

Система приводится к треугольному виду. Из последнего уравнения системы находим х₃ = 2, из второго х₂ = –1, из первого х₁ = 1. Система имеет единственное решение (1, –1, 2).

2. Дана система

2х₁ – х₂ + х₄ = 4,

4х₁ – 2х₂ + х₃ + х₄ = 7,

6х₁ – 3x₂ +2x₃ – x₄ = 8,

8x₁ – 4х₂ +3х₃ – х₄ = 11.

Замечание. При решении системы методом Гаусса неизвестные в уравнениях системы можно исключать не только с начала, но и с конца.

Именно таким образом мы и поступим при решении данной системы. Для этого умножим последнее уравнение последовательно на 1, 1, –1 и сложим с тремя первыми; получим равносильную систему

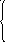8х₁ – 4х₂ + 3х₃ – х₄ = 11,

10х₁ – 5х₂ + 3х₃ = 15,

12х₁ – 6х₂ + 4х₃ = 18,

–2х₁ + х₂ – х₃ = –3.

Теперь умножим последнее уравнение последовательно на 3 и на 4 и прибавим к двум предыдущим; получим равносильную систему:

8х₁ – 4х₂ + 3х₃ – х₄ = 11,

–2х₁ + х₂ – х₃ = –3,

4х₁ – 2х₂ = 6,

4х₁ – 2х₂ = 6.

Далее, умножив предпоследнее уравнение на –1 и сложив его с последним, имеем:

8х₁ – 4х₂ + 3х₃ – х₄ = 11,

–2х₁ + х₂ – х₃ = –3,

4х₁ – 2х₂ = 6,

0х₁ – 0х₂ = 0.

Последнее уравнение есть тождество и его из системы можно исключить. Окончательно

8х₁ – 4х₂ + 3х₃ – х₄ = 11,

–2х₁ + х₂ – х₃ = –3,

2х₁ – х₂ = 3.

Таким образом, система приводится к трапецеидальному виду. Полагая х₁ вспомогательным неизвестным и придавая ему любые значения, например, , находим решение системы ( 2 –3  . Так как  может принимать любые значения из R, система не определена и имеет бесконечно много решений.