§3. Матричная и векторная формы записи линейных

УРАВНЕНИЙ. ТЕОРЕМА КРОНЕКЕРА – КАПЕЛЛИ

С системой (7.1) линейных уравнений можно связать следующие матрицы:

1.Матрицу А коэффициентов а_ij при неизвестных x₁, x₂, . . . , x_n системы.

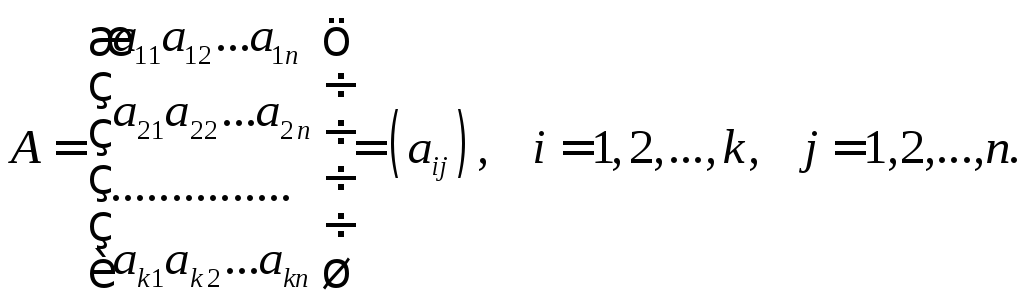
Эту матрицу называют основной.

2. Если к основной матрице А присоединить столбец свободных членов в₁,в₂,...,в_k системы, то получим так называемую расширенную матрицу А^* данной системы

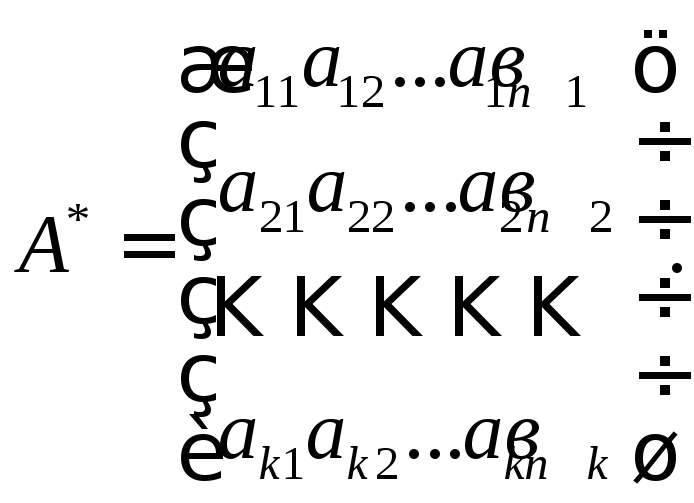
3. Матрицу-столбец свободных членов размер матрицыk 1.

4. Матрицу-столбец неизвестных 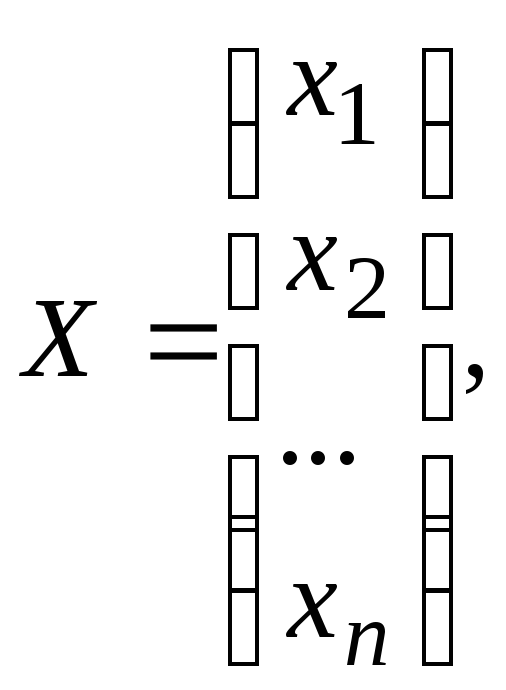размер матрицыn1.

Используя определение произведения матриц, систему (7.1) можно записать в виде

АХ = В (7.4)

Эта форма записи системы линейных уравнений называется матричной. Если при этом матрицу А рассматривать как некоторое отображение пространства Rⁿ в R^k, а матрицы Х и В ассоциировать с вектор-столбцами соответственно иТогда решение системы (7.1) можно свести к вопросу об установлении векторовкоторые являются прообразами векторапри отображенииRⁿ в R^k, заданном матрицей А, т.е.

Кроме матричной, систему линейных уравнений можно записать и в векторной форме. Для этого матрицу А связывают с системой из n вектор-столбцов в пространствеR^к.

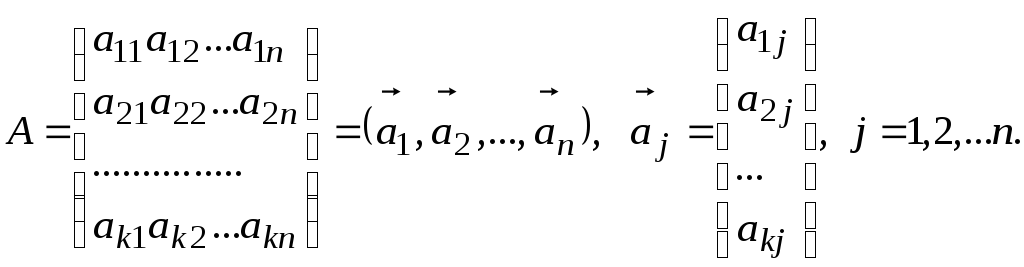
Тогда система (7.1) примет вид (7.5)

здесь

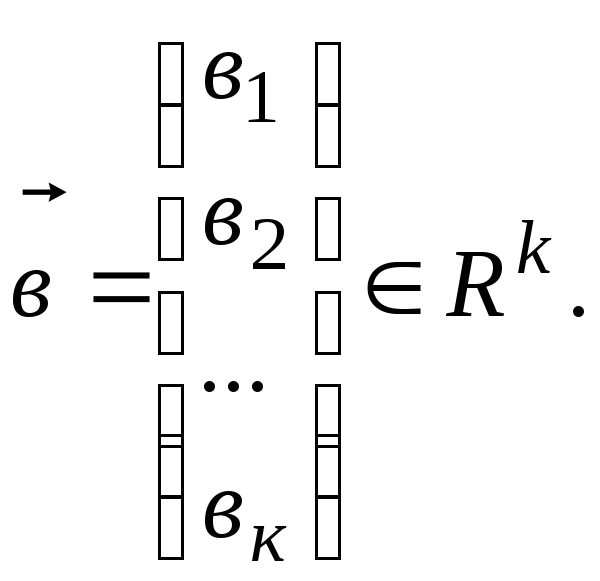
Исходя из уравнения (7.5) вопрос о решении системы (7.1) можно свести к вопросу об установлении линейной зависимости системы векторов . Так система (7.1) имеет решение, если векторалинейно зависимы. Действительно, из (7.5) следует, что векторявляется линейной комбинацией векторови, следовательно, он принадлежит подпространству, порожденному векторами. Если же векторне принадлежит подпространству, порожденному векторами, т.е. векторалинейно независимы, то система (7.1) решений не имеет. Другими словами система (7.1) имеет решение, если рангr^*(A^*) системы векторов не превышает рангаr(A) системы векторов , а это означает, что они должны быть равны. Теперь если систему векторовсвязать с расширенной матрицейA^*, то вышесказанное можно рассматривать как доказательство следующей теоремы.

Теорема Кронекера – Капелли (условие совместимости системы линейных уравнений): Система линейных уравнений разрешима (совместна) тогда и только тогда, когда ранг r(A) основной матрицы А равен рангу r^*(A^*) расширенной матрицы A^*: r(A) = r^*(A^*).

§4. Система крамера

Допустим, что число уравнений в системе (7.1) равно числу неизвестных (k = n) и что вектор-столбцы изRⁿ линейно независимы; в этом случае (7.1) называется системой Крамера.

Поскольку вектор-столбцы линейно независимы, то они составляют базис пространстваRⁿ, следовательно, всякий вектор-столбец представляется и притом единственным способом, в форме (7.5). Таким образом, система Крамера всегда имеет решение, и притом единственное.

Для нахождения этого решения запишем систему Крамера в матричной форме (7.4): АХ = В. Основная матрица А системы Крамера – квадратная, порядка п, и ее определитель отличен от нуля: D(A)  , так как вектор-столбцы матрицы линейно независимы. Поэтому матрица А имеет обратную матрицу ^. Умножим обе части уравнения (7.4) на ^ слева:

^AX = ^B.

Поскольку ^A = E и EX = X, то X = ^B или

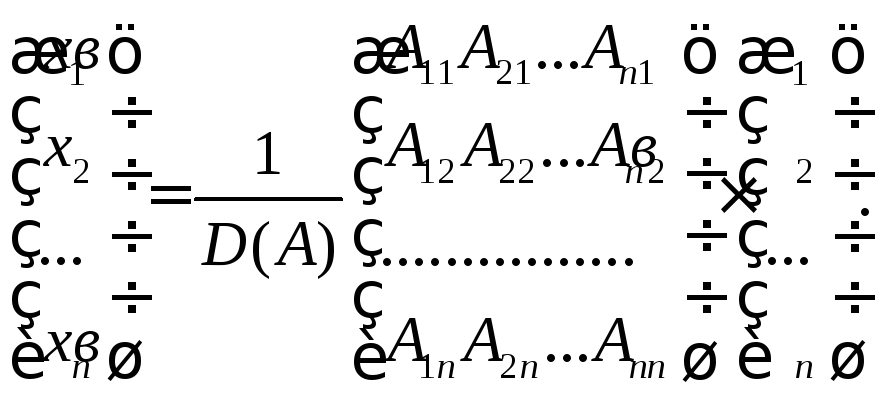
Перемножая ^ на B, получаем

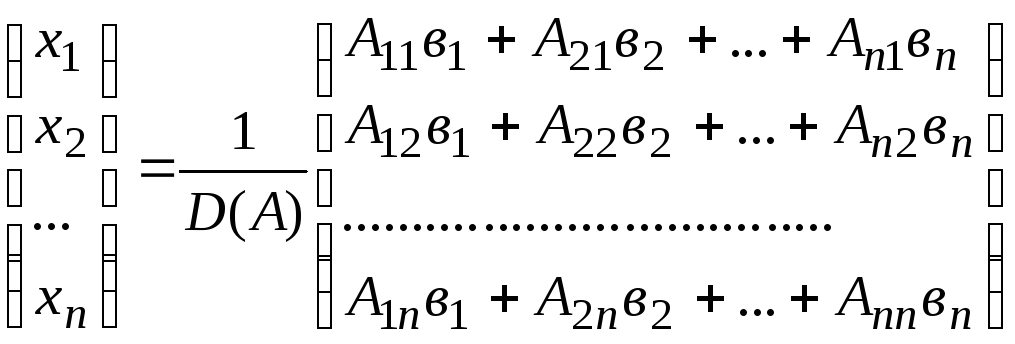. (7.6)

Откуда ,

где j = 1, 2,...,n, а A_1jв₁ + A_2jв₂ +....+ A_njв_n – определитель матрицы, которая получена из основной A путем замены элементов j-го столбца, т.е. коэффициентов при определяемом неизвестном x_j на столбец свободных членов в₁, в₂,...,в_n системы. Таким образом,

.

Теперь вышесказанное сформулируем в виде следующего правила.

Правило Крамера. Если определитель D(A) основной матрицы А системы из n линейных уравнений с n неизвестными отличен от нуля (D(A) то система имеет единственное решение и это решение определяется по формуле:

,j = 1,2, ..., n, (7.7)

где D(A_j) – определитель, полученный из D(A) заменой j-го столбца, столбцом свободных членов системы.

Пример. Решить систему уравнений.

3x – 3y + 2z = 2,

4x – 5y + 2z = 1,

5x – 6y + 4z = 3.

Вычислим определитель основной матрицы А:

.

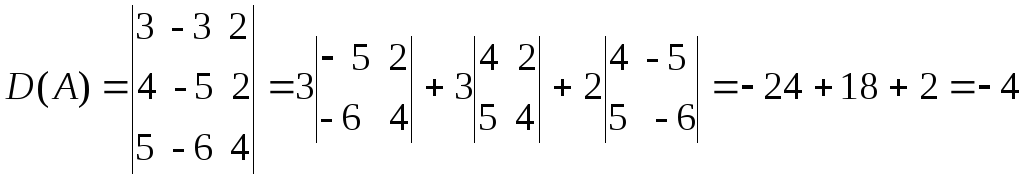Так как D(A)   , то это система Крамера и, следовательно, она имеет одно решение, которое ищем по формуле:

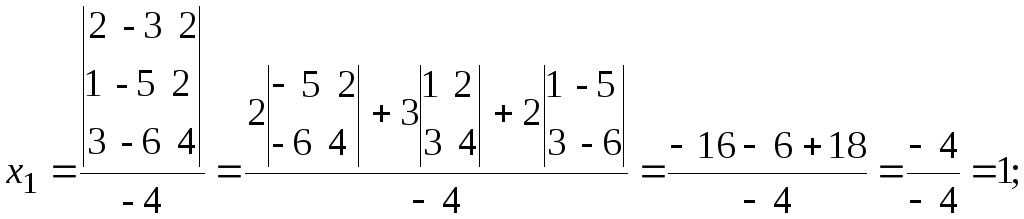
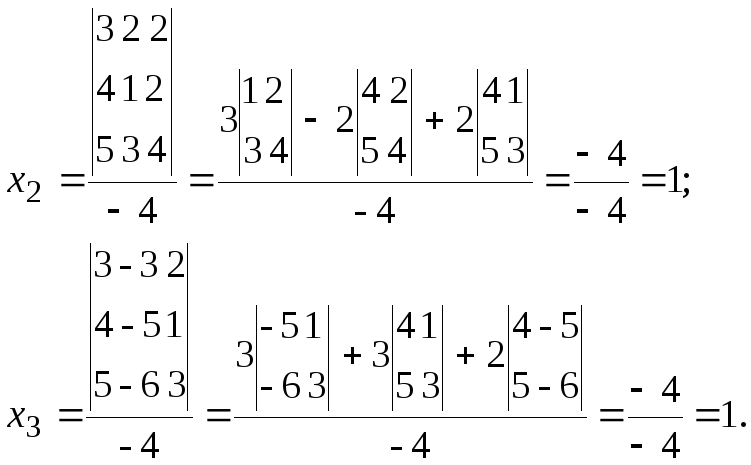
Ответ: х₁ = х = 1; х₂ = у = 1; х₃ = z = 1.