2.2. Приведение квадратной матрицы к диагональной форме

Собственные векторы линейного отображенияf, принадлежащие к различным собственным значениям этого отображения, будучи линейно независимыми, могут образовать базис пространства К размерности n. Это возможно, например, если отображение f имеет n различных собственных значений; допустим, что это имеет место; обозначим их через __ . . .,_n. Все они служат простыми нулями характеристического многочлена.

Пусть – собственные векторы, принадлежащие соответственно собственным значениям, образуют базис пространстваК. В принципе может случиться, что линейное отображение имеет меньше чем n собственных значений, но все же имеет базис из собственных векторов.

Пусть есть произвольный вектор изК, а  – соответствующий вектор в Сⁿ. Имеем Отсюда следует, что соответствующим вектором вСⁿ будет вектор ; стало быть, он получается изпри помощи диагональной матрицы



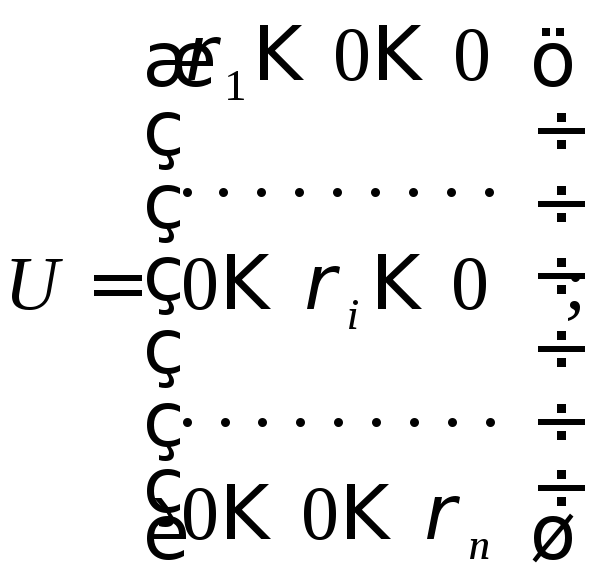
Таким образом, если в качестве базиса в К берутся собственные векторы , то отображение пространстваСⁿ в Сⁿ, соответствующее отображению f, задается диагональной матрицей U. Если же – произвольный базис в К, то

дляj =1,2, . . ., n и матрица перехода

.

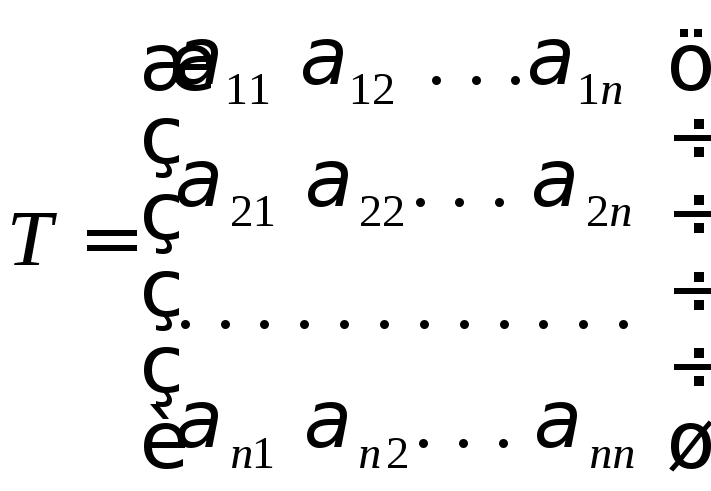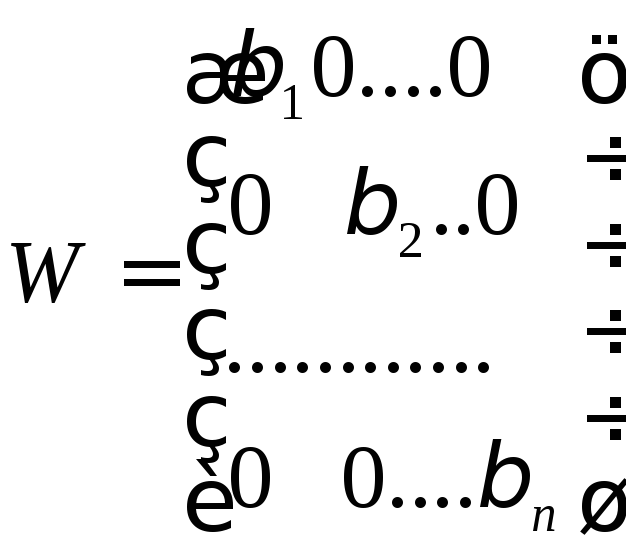Пусть А – матрица, представляющая отображение f , когда в качестве базиса в К взяты ; тогдаU = T^–1AT. Следовательно, существует такая обратимая матрица Т, что матрица, преобразованная из А посредством Т, будет диагональной матрицей U. Матрица U не единственная, ибо можно изменять порядок векторов ; однако, если существует диагональная матрица, преобразованная изА, то ,

т.е. (книга 2, гл.3, §4), (–1)ⁿ(  __)(_n)=( –1)ⁿ(–_)__n), стало быть, числа _ _ ,...,_n являются, с точностью до порядка следования, собственными значениями, а W есть одна из матриц вида U.

Заметим, что векторное подпространство собственных векторов, принадлежащих одному собственному значению, имеет размерность, равную единице. Действительно, если и – два собственных вектора, принадлежащих собственному значению _, то оба они принадлежат векторному подпространству, являющемуся дополнением (n – 1)-мерного векторного пространства, порожденного векторами , а значит, векторному подпространству размерности единица. Следовательно,,(при этом   ).

Если не все собственные значения различны, то не всегда можно найти диагональную матрицу, представляющую линейное отображение. Однако и в этом случае можно найти матрицу, выявляющую собственные значения и имеющую форму, удобную для вычислений. Для рассмотрения этого случая отсылаем читателя к специальной литературе.

Для вещественного пространства Rⁿ комплексные корни характеристического уравнения не могут быть собственными значениями, так как для них не имеет смысла равенство , поскольку координаты вектораи элементы матрицыА принадлежат полю R действительных чисел. Поэтому линейное отображение Rⁿ в Rⁿ, заданное матрицей А над полем R действительных чисел, для которой характеристическое уравнение имеет только комплексно сопряженные корни (т.е. ни одного вещественного корня) собственных значений не имеет (степень такого характеристического многочлена должна быть четной). Однако, если линейное отображение Rⁿ в Rⁿ задано симметрической матрицей А, то все корни характеристического уравнения такой матрицы действительны; все принадлежащие им собственные векторы могут быть выбраны действительными. В этом случае собственные векторы матрицы А образуют базис, и в этом базисе матрица линейного отображения имеет диагональный вид. Рассмотрим это на примере приведения к диагональному виду симметрической действительной матрицы А, определяющей квадратичную форму на Rⁿ.