§6. Неоднородная система линейных уравнений

Если в системе линейных уравнений (7.1) хотя бы один из свободных членов в_i отличен от нуля, то такая система называется неоднородной.

Пусть задана неоднородная система линейных уравнений, которую в векторной форме можно представить в виде

, i = 1,2,...,к, (7.13)

Рассмотрим соответствующую однородную систему

i = 1,2,...,к. (7.14)

Пусть вектор является решением неоднородной системы (7.13), а векторявляется решением однородной системы (7.14). Тогда, легко видеть, что вектортакже является решением неоднородной системы (7.13). Действительно

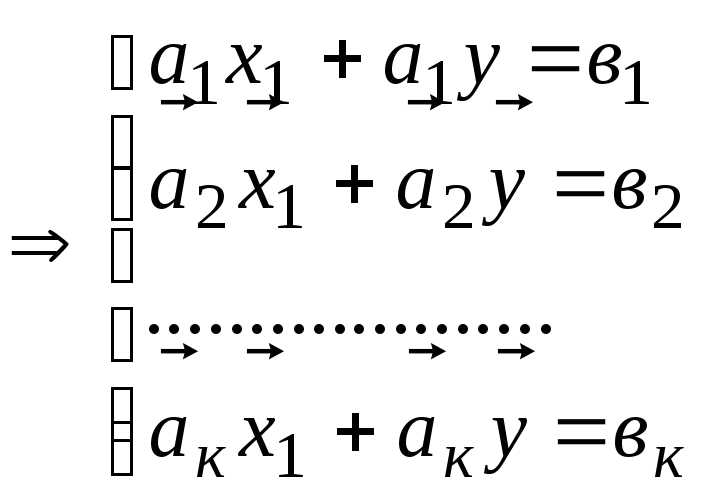
Теперь, используя формулу (7.12) общего решения однородного уравнения, имеем

а потому

(7.15)

где любые числа изR, а – фундаментальные решения однородной системы.

Таким образом, решение неоднородной системы есть совокупность ее частного решения и общего решения соответствующей однородной системы.

Решение (7.15) называется общим решением неоднородной системы линейных уравнений. Из (7.15) следует, что совместная неоднородная система линейных уравнений имеет единственное решение, если ранг r(A) основной матрицы А совпадает с числом n неизвестных системы (система Крамера), если же r(A)  n, то система имеет бесчисленное множество решений и эта совокупность решений эквивалентна подпространству решений соответствующей однородной системы уравнений размерности n – r.

Примеры.

1. Пусть дана неоднородная система уравнений, в которой число уравнений к = 3, а число неизвестных n = 4.

х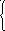₁ – х₂ + х₃ –2х₄ = 1,

х₁ – х₂ + 2х₃ – х₄ = 2,

5х₁ – 5х₂ + 8х₃ – 7х₄ = 3.

Определим ранги основной матрицы А и расширенной А^* данной системы. Поскольку А и А^* не нулевые матрицы и к = 3  n, поэтому 1  r (A), r^*(А^*)  3. Рассмотрим миноры второго порядка матриц А и А^* :

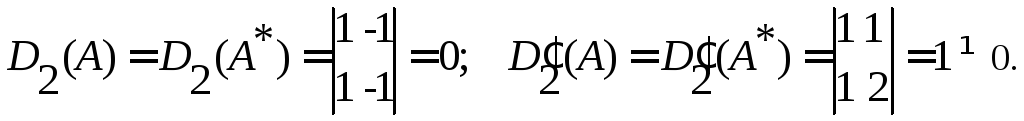
Таким образом, среди миноров второго порядка матриц А и А^* есть минор отличный от нуля, поэтому 2  r(A), r^*(A^*)  3. Теперь рассмотрим миноры третьего порядка

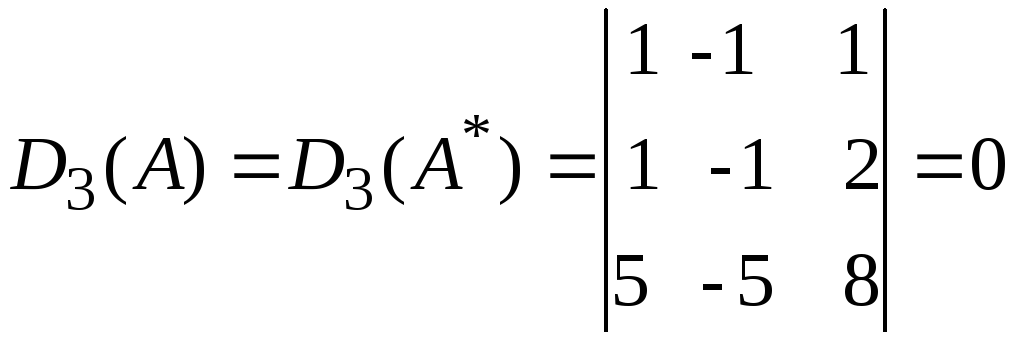, так как первый и второй столбец пропорциональны. Аналогично и для минора .

.

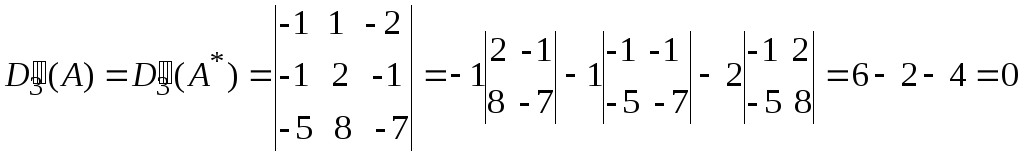И так все миноры третьего порядка основной матрицы А равны нулю, следовательно, r(A) = 2. Для расширенной матрицы А^* еще имеются миноры третьего порядка

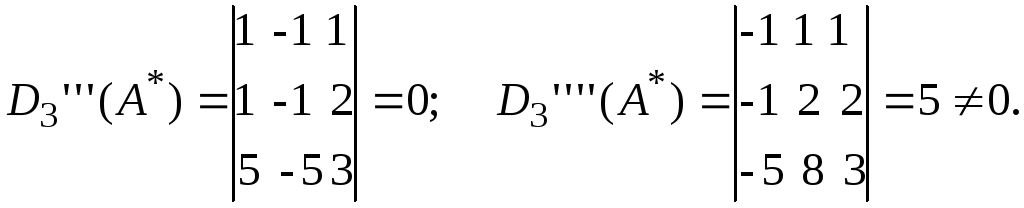
Следовательно, среди миноров третьего порядка расширенной матрицы А^* есть минор отличный от нуля, поэтому r^*(A^*) = 3. Это означает, что r(A)  r^*(A^*) и тогда, на основании теоремы Корнекера – Капелли, делаем вывод, что данная система несовместна.

2. Решить систему уравнений

3х₁ + 2х₂ + х₃ + х₄ = 1,

3х₁ + 2х₂ – х₃ – 2х₄ = 2.

Для данной системы и поэтому 1 r(A), r^*(A^*)  2. Рассмотрим для матриц  A и  A^* миноры второго порядка

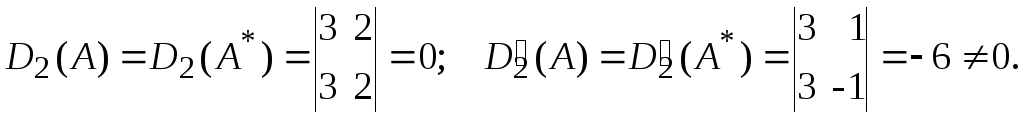Таким образом, r(A) = r^*(A^*) = 2, и, следовательно, система совместна. В качестве базовых выберем любые две переменные, для которых минор второго порядка, составленный из коэффициентов у этих переменных не равен нулю. Такими переменными могут быть, например,

х₃ и х₄, так как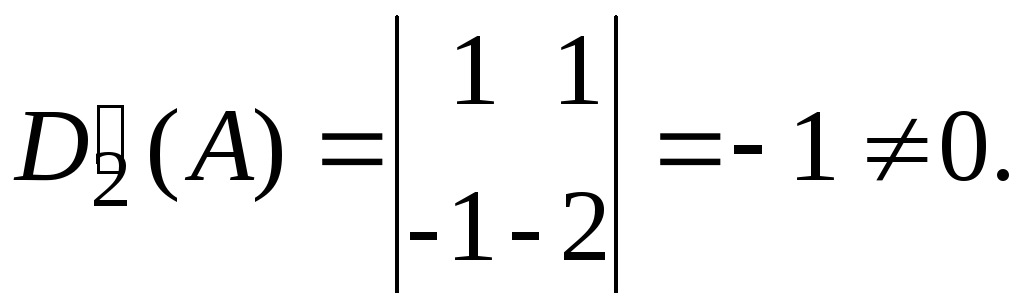Тогда имеем

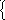х₃ + х₄ = 1 – 3х₁ – 2х₂,

– х₃ – 2х₄ = 2 – 3х₁ – 2х₂.

Определим частное решение неоднородной системы. Для этого положимх₁ = х₂ = 0.

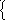х₃ + х₄ = 1,

– х₃ – 2х₄ = 2.

Решение этой системы: х₃ = 4, х₄ = – 3, следовательно, = (0,0,4, –3).

Теперь определим общее решение соответствующего однородного уравнения

х₃ + х₄ = – 3х₁ – 2х₂,

–х₃ – 2х₄ = – 3х₁ – 2х₂.

Положим: х₁ = 1, х₂ = 0

х₃ + х₄ = –3,

–х₃ – 2х₄ = –3.

Решение этой системы х₃ = –9, х₄ = 6.

Таким образом

Теперь положим х₁ = 0, х₂ = 1

х₃ + х₄ = –2,

–х₃ – 2х₄ = –2.

Решение: х₃ = – 6, х₄ = 4, и тогда

После того как определены частное решение , неоднородного уравнения и фундаментальные решенияисоответствующего однородного уравнения, записываем общее решение неоднородного уравнения.

где любые числа изR.