3.2. Смешанное произведение трех свободных векторов

Определение. Если вектор умножить скалярно на вектор, то полученное число называетсясмешанным произведением трех векторов и. Обозначается.

Нетрудно показать, что абсолютное значение смешанного произведения трех векторов равно объему V_p параллелепипеда, построенного на этих векторах, т.е.=V_p . Действительно, – площадьS параллелограмма, построенного на векторах , а– высотаh параллелепипеда, основанием которого есть параллелограмм площадью S, так как и. Следовательно,=V_p –объем параллелепипеда.

Выразим смешанное произведение (и объемV_p параллелепипеда) через координаты векторов. С учетом (6.2), а также, что и получаем

=·

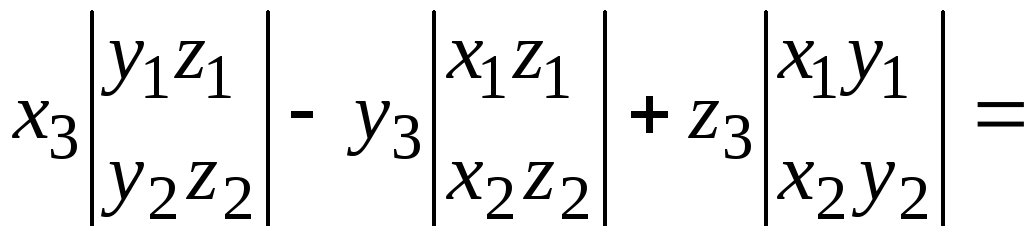
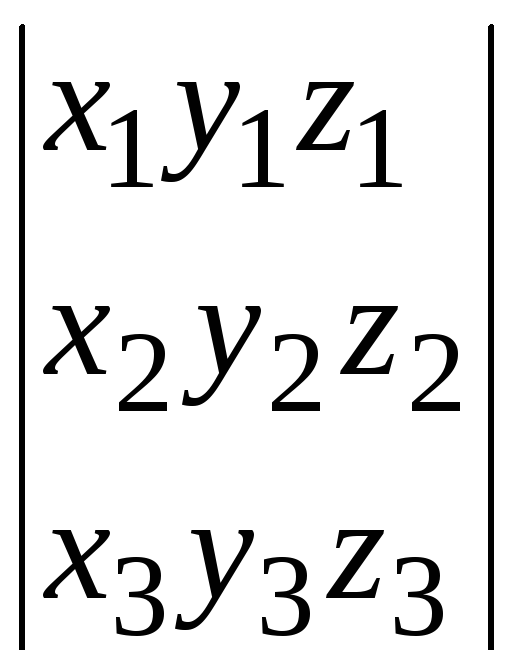= и V_p =

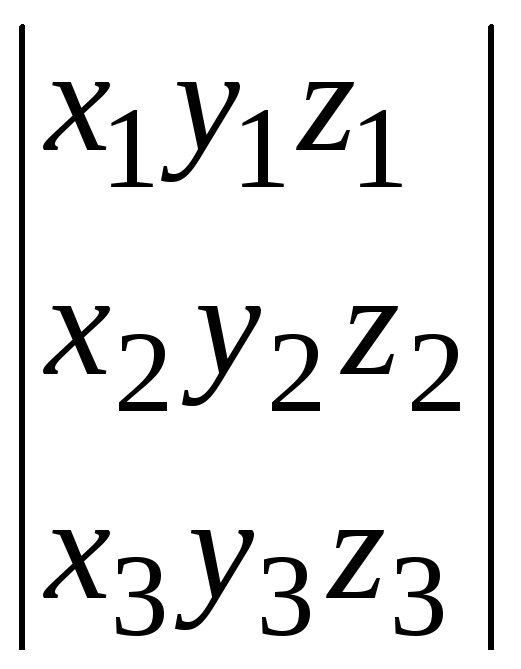
Таким образом, абсолютное значение определителя третьего порядка равно объему параллелепипеда, построенного на трех векторах, координаты которых в единичном ортонормированном базисе являются вектор-строками соответствующей матрицы и, соответственно, элементами строк определителя. В принципе, координаты векторов можно располагать и по столбцам матрицы (определителя), так как значение определителя при транспонировании матрицы не изменяется. Отсюда можно сделать следующеезаключение.

Для того чтобы три вектора были компланарны, необходимо и достаточно, чтобы определитель матрицы, заданной координатами этих векторов, в ортонормированном базисе был равен нулю.

Понятие параллелепипеда и определителя как его объема, распространяется на векторное пространство Rⁿ, размерность которого n > 3. Аналогичное образование из n векторов пространства Rⁿ и множества точек этого пространства, заключенных в границах этих векторов, рассматриваемых как объем, ограниченных этими векторами, называется параллелотопом.

Пусть параллелотоп образован n векторами , разложение которых по каноническому базисупространстваRⁿ имеет вид тогда объемтакого параллелотопа равен абсолютному значению определителяD(А), где А – квадратная матрица, у которой являются вектор-столбцами (вектор-строками), т.е.

.

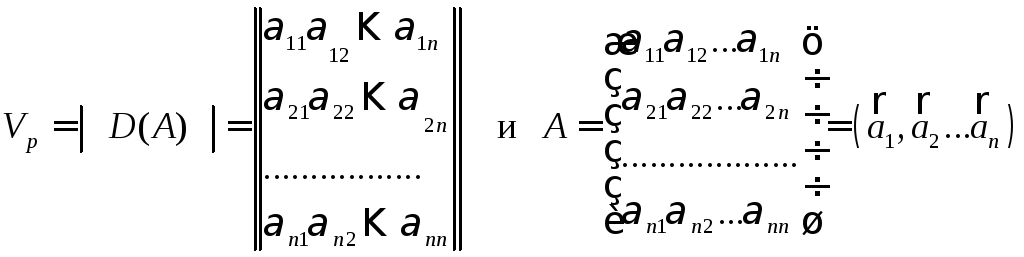§4. Применение определителей для нахождения ранга матриц

Рассмотрим матрицу А над полем Р размером mn и представим ее как систему из n вектор-столбцов в пространстве P^m.

Элементы матрицы а_ij – числа из Р. Для того, чтобы выяснить ранг r данной системы векторов или матрицы А, заданной координатами этих векторов, необходимо определить возможное наибольшее число линейно независимых векторов, которые можно выбрать из этой системы, или, другими словами, число базисных векторов этой системы.

Прежде рассмотрим частный случай, когда m = n. Покажем, что для такой квадратной матрицы порядка n справедлива следующая теорема.

Теорема 1. Для того чтобы n векторов из Рⁿ были линейно независимы, необходимо и достаточно, чтобы определитель квадратной матрицы А, составленный из координат этих векторов D(A) = D() .

Доказательство. Необходимость. Пусть линейно независимы, то матрицаА – обратима (книга 2, гл.5, §5, п.5.1), и значит, существует обратная ей матрица А^-1, такая, что А·А^-1 = Е, где Е – единичная матрица. Тогда воспользовавшись свойством перемножения определителей, получим: D(АА^-1) = = D(А)·D(А^-1) = D(Е) = 1, и, стало быть, D(А) ·D(А^-1) = 1, отсюда D(А)  0.

Достаточность. Утверждение, что если D(A)  , то система векторов линейно независима, эквивалентно утверждению, что если D(A) = 0, то система векторов линейно зависима. Докажем последнее. Так как D(A) = 0, то либо одна из строк или один из столбцов определителя равны нулю, либо две строки (столбца) определителя равны или пропорциональны, и, наконец, одна из строк (столбцов) определителя является линейной комбинацией других строк (столбцов) определителя. Для системы векторов это означает, что в системе существует либо нуль-вектор, либо два равных или пропорциональных вектора, либо вектор, являющийся линейной комбинацией других векторов системы. Во всех этих трех случаях, как следует из теорем о линейно зависимых и линейно независимых векторах, система векторовбудет линейно зависима, что и требовалось доказать.

Таким образом, из вышеприведенной теоремы следует, что если определитель D(A) квадратной матрицы A порядка n не равен нулю, то ранг матрицы А равен n: r(A) = n. Если же D(A) = 0, то r(A)  n.

Теперь мы обобщим полученный результат с тем, чтобы указать процесс, позволяющий находить точное значение ранга r(A) при помощи определителей для матрицы А любого размера. Этот процесс основан на теореме, для которой мы приведем только формулировку, а доказательство опустим. Но прежде чем дать формулировку теоремы, введем понятие основного и окаймляющих его миноров для матрицы А.

Определение 1. Минором порядка h матрицы А называется определитель из h строк и h столбцов, который получен в результате исключения строк и столбцов этой матрицы так, чтобы осталось только h строк и h столбцов, или другими словами, минор – это определитель квадратной матрицы составленный из элементов расположенных на пересечении h различных строк и h различных столбцов исходной матрицы.

Ясно, что наивысший порядок минора матрицы размером mn равен минимальному числу из m или n, h_max = min (m, n).

Определение 2. Если h  min (m, n), то к матрице порядка h можно присоединить еще i строк и i столбцов исходной матрицы, где i=1,2,...,min(m, n) – h и получать миноры более высших h + i порядков. Такие миноры называются окаймляющими для основного минора h.

Определение 3. Если в качестве основного минора матрицы

,

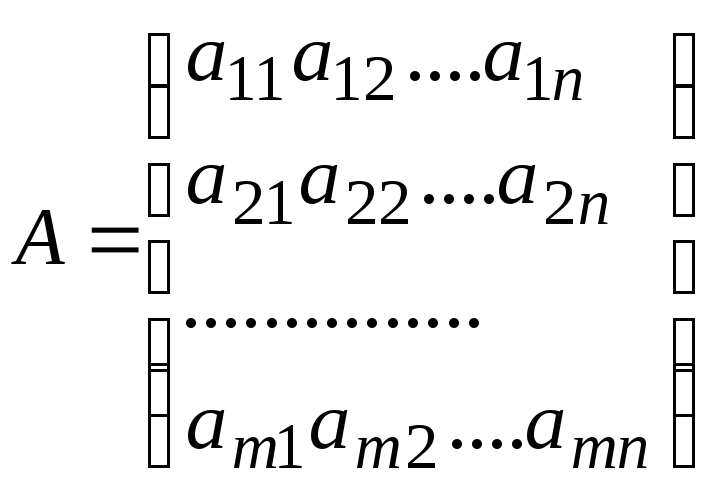выбрать минор 1-го порядка, расположенный в верхнем левом углу а₁₁, то все окаймляющие его миноры высших порядков, получаемые присоединением соседних строк и столбцов, называются главными минорами матрицы А.

где S = min (m, n).

Справедлива следующая теорема.

Теорема 2. Если в матрице А существует минор r-го порядка не равный нулю, а все миноры (r + 1)-го порядка, окаймляющие этот минор, равны нулю, то r есть ранг матрицы А: r = r(A). Минор порядка r, отличный от нуля называется базисным.

Замечание. Если все миноры (r + 1)-го порядка равны нулю, то и все миноры более высоких порядков также равны нулю.

С учетом этой теоремы процесс определения ранга матрицы сводится к следующему. В матрице необходимо выбрать в качестве основного минор любого порядка, отличный от нуля. Затем нужно вычислить окаймляющие его миноры более высоких порядков. Тогда наивысший порядок окаймляющего минора, отличного от нуля, и будет являться рангом рассматриваемой матрицы.

Пример. Определить ранг матрицы . Выберем в качестве основного, минор 1-го порядка расположенный в верхнем левом углу |1| . Окаймляющий его минор второго порядка а окаймляющие миноры третьего порядка

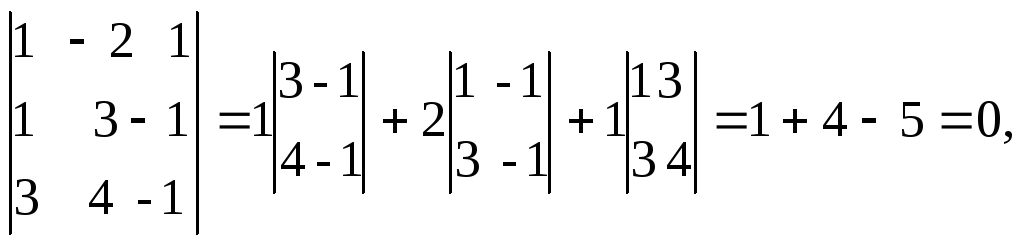
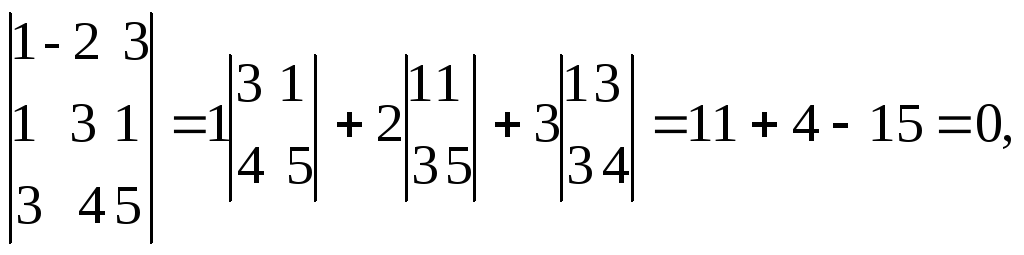
Следовательно, ранг матрицы А: r(A) = 2.

Замечание. Если в качестве основного минора выбрать другой минор отличный от нуля, но расположенный в другом месте матрицы, результат был бы тот же.