
- •Линейная алгебра глава 1 законы композиции
- •§1. Внутренние законы композиции
- •1.2. Основные алгебраические образования: группы, кольца, поля
- •§2. Внешние законы композиции
- •§3. Изоморфизм
- •Глава 2 комплексные числа
- •§1. Поле с комплексных чисел
- •§2. Комплексно сопряженные числа
- •§3. Модуль комплексного числа. Деление двух комплексных чисел
- •§4. Геометрическая интерпретация комплексных чисел
- •§5. Тригонометрическая форма комплексного числа. Формула муавра. Извлечение корня
- •§6. Комплексные функции
- •Комплексные функции одного действительного переменного
- •Показательная функция zеz с комплексным показателем и ее свойства
- •Формулы Эйлера. Показательная форма комплексного числа
- •Глава 3 многочлены
- •§1. Кольцо многочленов
- •§2. Деление многочленов по убывающим степеням
- •§3. Взаимно простые и неприводимые многочлены. Теорема и алгоритм евклида
- •§4. Нули (корни) многочлена. Кратность нуля. Разложение многочлена в произведение неприводимых многочленов над полем с и r
- •Упражнения
- •Глава 4 векторные пространства
- •§1. Векторное пространство многочленов над полем p коэффициентов
- •§2. Векторные пространства р n над полем р
- •§3. Векторы в геометрическом пространстве
- •3.1. Типы векторов в геометрическом пространстве
- •Из подобия треугольников авс и ав'с' следует (как в случае , так и в случае ), что.
- •3.3. Задание свободных векторов при помощи декартовой системы координат и соответствие их с векторами из векторного пространства r3
- •3.4. Скалярное произведение двух свободных векторов
- •Упражнения
- •§4. Векторное подпространство
- •4.1. Подпространство, порожденное линейной комбинацией векторов
- •4.2. Линейная зависимость и независимость векторов
- •4.3. Теоремы о линейно зависимых и линейно независимых векторах
- •4.4. База и ранг системы векторов. Базис и размерность векторного подпространства, порожденного системой векторов
- •4.5. Базис и размерность подпространства, порожденного системой
- •§5. Базис и размерность векторного пространства
- •5.1. Построение базиса
- •5.2. Основные свойства базиса
- •5.3. Базис и размерность пространства свободных векторов
- •§6. Изоморфизм между n – мерными векторными пространствами к и р n над полем р
- •§8. Линейные отображения векторных пространств
- •8.1. Ранг линейного отображения
- •8.2. Координатная запись линейных отображений
- •Упражнения
- •Глава 5 матрицы
- •§1. Ранг матрицы. Элементарные преобразования матриц
- •§2. Алгебраичесие операции над матрицами.
- •Пусть даны матрицы
- •§3. Изоморфизм между векторным пространством
- •§4. Скалярное произведение двух векторов из пространства Rn
- •§5. Квадратные матрицы
- •5.1. Обратная матрица
- •5.2. Транспонированная квадратная матрица.
- •Упражнения
- •Глава 6 определители
- •§1. Определение и свойства определителя, вытекающие из определения
- •§2. Разложение определителя по элементам столбца (строки). Теорема о чужих дополнениях
- •§3. Геометрическое представление определителя
- •3.1. Векторное произведение двух свободных векторов
- •3.2. Смешанное произведение трех свободных векторов
- •§4. Применение определителей для нахождения ранга матриц
- •§5. Построение обратной матрицы
- •Упражнения
- •Глава 7 системы линейных уравнений
- •§1. Определения. Совместные и несовместные системы
- •§2. Метод гаусса
- •§3. Матричная и векторная формы записи линейных
- •3. Матрицу-столбец свободных членов размер матрицыk 1.
- •§4. Система крамера
- •§5. Однородная система линейных уравнений
- •§6. Неоднородная система линейных уравнений
- •Упражнения
- •Глава 8 приведение матриц
- •§1. Матрица перехода от одного базиса к другому
- •1.1. Матрица перехода, связанная с преобразованием
- •1.2. Ортогональные матрицы перехода
- •§2. Изменение матрицы линейного отображения при замене базисов
- •2.1. Собственные значения, собственные векторы
- •2.2. Приведение квадратной матрицы к диагональной форме
- •§3. Вещественные линейные и квадратичные формы
- •3.1. Приведение квадратичной формы к каноническому виду
- •3.2. Определенная квадратичная форма. Критерий Сильвестра
- •Упражнения
Упражнения
1. Решить методом Гаусса и с помощью определителей систему уравнений
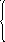 2х1
+ х2
+ 3х3
+ 4х4
= 11,
2х1
+ х2
+ 3х3
+ 4х4
= 11,
7х1 + 3х2 + 6х3 + 8х4 = 24,
3х1 + 2х2 + 4х3 + 5х4 = 14,
х1 + х2 + 3х3 + 4х4 = 10.
2. Найти базис и размерность подпространства, образуемого совокупностью решений однородной системы уравнений:
а
 )
3х1
+ 5х2
– х3
+ 2х4
= 0, б) х1
+ 4х2
– 3х3
+ 6х4
= 0,
)
3х1
+ 5х2
– х3
+ 2х4
= 0, б) х1
+ 4х2
– 3х3
+ 6х4
= 0,
2х1 + 4х2 – х3 + 3х4 = 0, 2х1 + 5х2 + х3 + 2х4 = 0,
х1 + 3х2 – х3 + 4х4 = 0; х1 + 7х2 – 10х3 + 20х4 = 0.
3. Совместна ли система уравнений? Если совместна, то решить ее:
а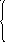
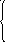 )х1
+ х2
+ х3
= 3, б) х1
– 2х2
– 3х3
= –3,
)х1
+ х2
+ х3
= 3, б) х1
– 2х2
– 3х3
= –3,
х1 + х2 – 3х3 = –1, х1 + 3х2 – 5х3 = 0,
2х1 + х2 – 2х3 = 1, –х1 + 4х2 + х3 = 3,
х1 + 2х2 – 3х3 = 1; 3х1 + х2 – 13х3 = – 6;
в
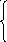 )
2х1
+ х2
– х3
– х4
+ х5
= 1, г) 2х1
– х2
+ х3
– 5х4
= 4,
)
2х1
+ х2
– х3
– х4
+ х5
= 1, г) 2х1
– х2
+ х3
– 5х4
= 4,
х1 – х2 + х3 + х4 – 2х5 = 0, 2х1 + 3х2 – 3х3 + х4 = 2,
3х1 + 3х2 – 3х3 – 3х4 + 4х5 = 2, 8х1 – х2 + х3 – х4 = 1,
4х1 + 5х2 – 5х3 – 5х4 + 7х5 = 3; 4х1 – 3х2 + 3х3 + 3х4 = 2;
д )х1
+ 2х2
+ х3
– х4
+ х5
= –1,
)х1
+ 2х2
+ х3
– х4
+ х5
= –1,
2х1 + 5х2 + 6х3 – 5х4 + х5 = 0,
х1 – 2х2 + х3 – х4 – х5 = 3,
х1 + 3х2 +2х3 – 2х4 + х5 = –1,
х1 – 4х2 + х3 + х4 – х5 = 3.
Найти с помощью обратной матрицы решение системы
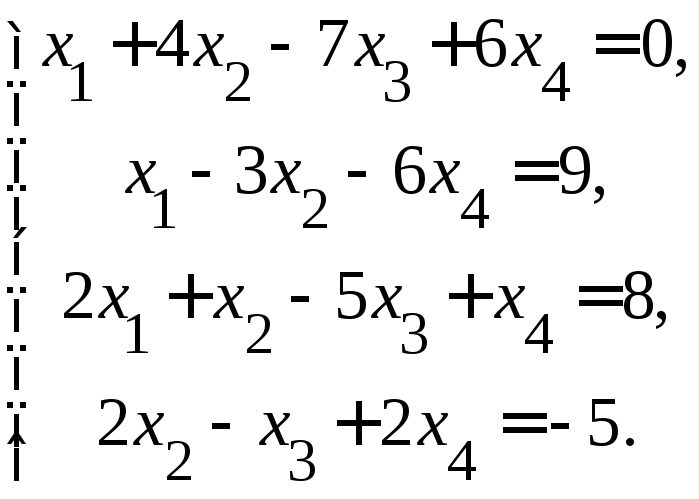
Глава 8 приведение матриц
Пусть К есть векторное пространство конечной размерности n над полем Р. И пусть f есть линейное отображение пространства К в К. При помощи обычного изоморфизма пространств К и Pn приходим к линейному отображению Pn в Pn. Это отображение определяет квадратную матрицу из n строк и n столбцов, зависящую от выбранного в K базиса. Попытаемся найти в K такой конкретный базис, относительно которого связанная с f матрица имела бы наиболее простую форму.
§1. Матрица перехода от одного базиса к другому
Пусть
![]() – первоначальный базис пространстваК,
а
– первоначальный базис пространстваК,
а
![]() – его новый базис. Выразим векторы
– его новый базис. Выразим векторы![]() через векторы
через векторы![]() ,
образующие первый базис. Имеем
,
образующие первый базис. Имеем![]() ,j = 1,
2, ..., n.
Координаты
,j = 1,
2, ..., n.
Координаты
![]() векторов
векторов![]() в базисе
в базисе![]() можно записать в виде матрицы:
можно записать в виде матрицы:
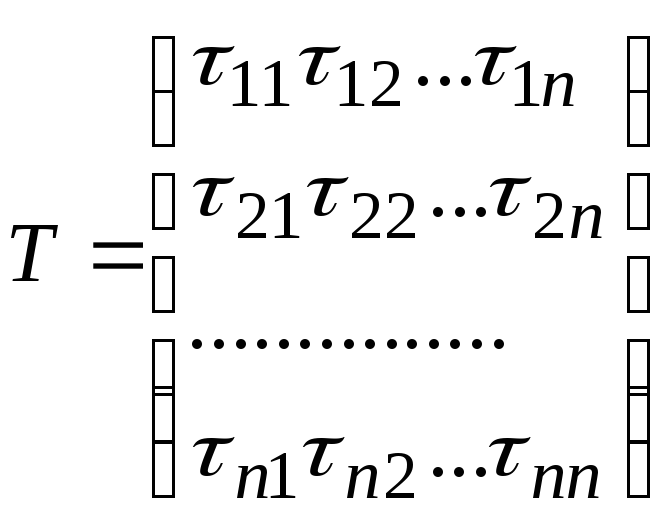 ,
,
здесь
столбцы матрицы – это координаты
векторов
![]() по базису
по базису![]() .
.
Определение. Матрицу Т, вектор-столбцы которой составлены из координат векторов нового базиса, выраженных через первоначальный базис, называют матрицей перехода от одного базиса к другому.
Матрица перехода Т обладает следующими свойствами:
1.
Поскольку
![]() и
и![]() – базисы одного и того же пространстваК,
то число их одинаково, а разложение по
базису единственно. Поэтому матрица Т
всегда квадратная и определяется
однозначно.
– базисы одного и того же пространстваК,
то число их одинаково, а разложение по
базису единственно. Поэтому матрица Т
всегда квадратная и определяется
однозначно.
2.
Вектор-столбцы матрицы Т
линейно независимы (это вектора базиса).
Таким образом, ранг r(T)
матрицы перехода T
равен n;
это означает, что определитель D(T)
и матрица T
всегда имеет обратную T–1,
которая будет матрицей перехода от
![]() к
к![]() .
.
Матрица перехода Т представляет взаимно однозначное отображение
![]() пространства
Pn
на себя.
Действительно, пусть
пространства
Pn
на себя.
Действительно, пусть
![]() – произвольный элемент изК.
Имеем
– произвольный элемент изК.
Имеем
![]()
выразив
![]() иТ,
получим
иТ,
получим
![]()
Векторы
![]() и
и![]() принадлежат пространствуPn,
и при этом
принадлежат пространствуPn,
и при этом
![]() .
Разложение по базисам единственно и
обратимо (существует обратная матрицаT–1),
следовательно
.
Разложение по базисам единственно и
обратимо (существует обратная матрицаT–1),
следовательно
![]() – взаимно однозначное отображение.
– взаимно однозначное отображение.
В качестве наглядной иллюстрации матрицы перехода рассмотрим ее для геометрического пространства, в котором матрица перехода связана с преобразованием системы координат и определяет линейное отображение R3 на R3.
