§2. Разложение определителя по элементам столбца (строки). Теорема о чужих дополнениях

Определение 1. Дополнительным минором некоторого элемента а_ij квадратной матрицы А порядка n, называется определитель D_ij матрицы порядка n – 1, которая получается из данной матрицы А вычеркиванием i-ой строки и j-го столбца (пересекающихся на этом элементе).

Пример. 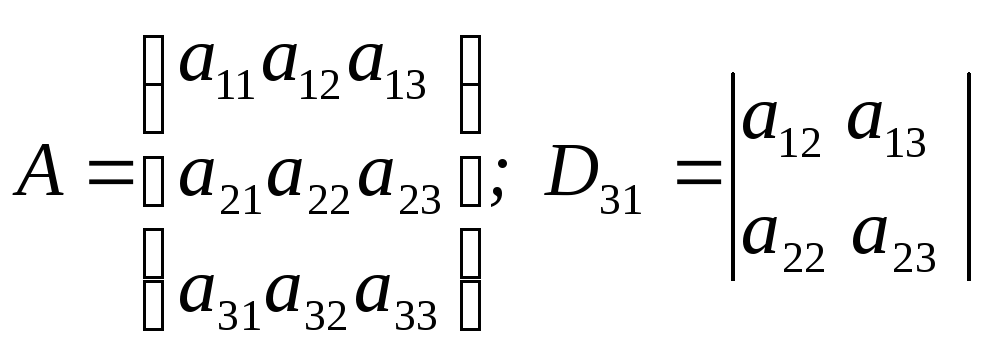– дополнительный минор элементаа₃₁.

Определение 2. Алгебраическим дополнением А_ij элемента а_ij называется его дополнительный минор D_ij умноженный на (–1)^i+j

А_ij = (–1)^i+j· D_ij

Справедливо следующее утверждение, которое мы примем без доказательства: если элементы некоторой строки (столбца) умножить на их алгебраические дополнения и эти произведения сложить, то получится величина определителя.

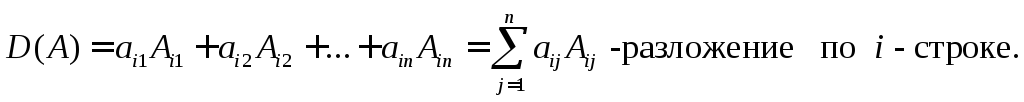
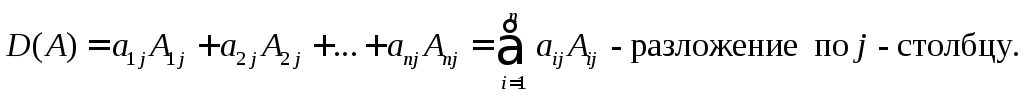
Данные разложения позволяют вычисление определителя порядка n свести к вычислению n определителей порядка n – 1. Кроме этих формул часто бывает, полезна и следующая теорема.

Теорема (о чужих дополнениях). Если элементы некоторой строки (столбца) умножить на алгебраические дополнения соответствующих элементов другой строки (столбца) и эти произведения сложить, то сумма будет равна нулю.

a_ij , где j = 1,2,...,n – элементы i-ой строки, а А_кj, где j = 1,2,...,n алгебраические дополнения элементов к-ой строки.

Доказательство. Рассмотрим определитель матрицы В, которая получается из матрицы А заменой элементов к-ой строки на элементы i-ой строки. Поскольку это определитель с двумя равными строками, то он равен нулю

Заметим, что в_кj = а_ij, а В_кj = А_кj, тогда , что и требовалось доказать.

Пример. .

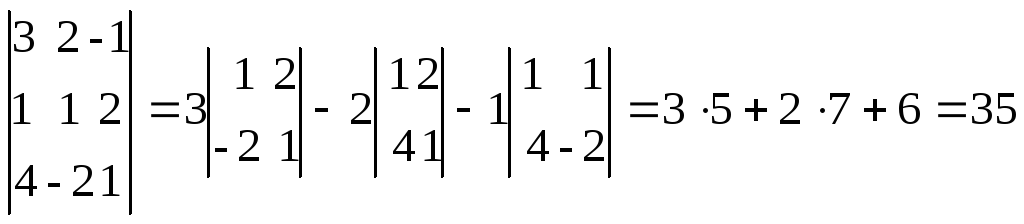Теперь дадим геометрическую интерпретацию определителю.

§3. Геометрическое представление определителя

Рассмотрим упорядоченную тройку некомпланарных свободных векторов и поставим им в соответствие упорядоченную тройку направленных отрезковисходящих из одной точки в ориентированном пространстве. На этих направленных отрезках, как на сторонах, построим параллелепипед (рис.2.6).

Имеется бесконечное множество ориентированных параллелепипедов, каждому из которых ставится в соответствие та же упорядоченная тройка векторов. Эти параллелепипеды получаются переносами любого из них и имеют, поэтому один и тот же объемV_p. Если вектора компланарны, то объем такого вырожденного параллелепипеда принимается равным нулю.

у

Z

С

В

D А

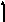
х

Рис. 2.6

Определим объем V_p параллелепипеда, построенного на векторах , в координатах. Для этого выберем в пространстве ортонормированный базиссвязав с ним систему координатx, y, z (рис.2.6). И пусть относительно этого базиса три вектора заданы своими координатами:

.

Введем две операции над свободными векторами.

3.1. Векторное произведение двух свободных векторов

Определение. Векторным произведением двух векторов называется вектортакой, что а)– угол между векторами, б)в) если, то векторы,образуют правую тройку. Векторное произведение обозначается

Согласно условию а) тогда и только тогда, когда векторыколлинеарны. Поэтому для множества векторов пространстваR¹ векторное произведение будет состоять только из одного нулевого вектора. Если же , точисленно равен площади параллелограмма, построенного на векторах, приведенных к общему началу (рис.2.7). Следует отметить, что в отличие от скалярного произведенияявляющегося отображением в R, векторное произведение, как и сложение, представляет внутренний закон композиции для пространства свободных векторов R³.

Основные свойства векторного произведения сводятся к следующим:

1. – не коммутативно;

2.

3. – дистрибутивно относительно сложения;

4. Нейтрального элемента не существует.



Рис. 2.7

Рассмотрим, как векторное произведение представляется в координатной форме.

Раскрывая скобки и учитывая, что

а получаем

Отсюда 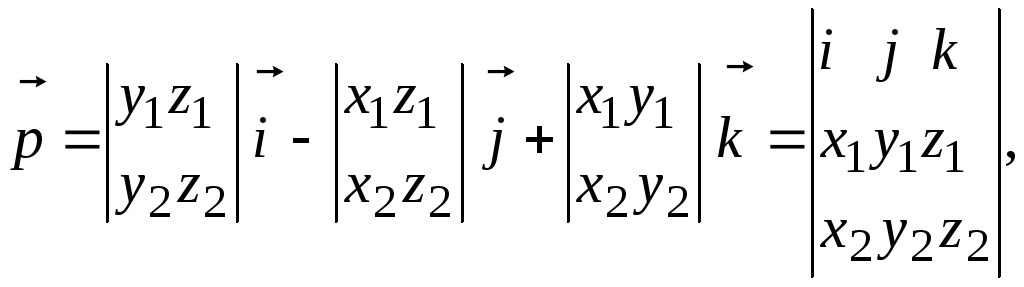(6.2)

Здесь , координаты вектора.