1.6.6. Биномиальный закон распределения

Если вероятность наступления какого-либо случайного события в каждом испытании равна р, то вероятность того, что при n испытаниях это событие осуществится m раз, определяется т.н. формулой Бернулли

, (1.123)

где

– (1.124)

число сочетаний из n по m;

. (1.125)

Закон распределения случайной величины, которая может принимать (n+1) значение (0, 1, 2, … , n), называется биномиальным законом распределения.

Для биномиального закона распределения математическое ожидание M(X) = np, дисперсия D = npq.

Пример 1.22. Из генеральной совокупности наугад было отобрано четыре пробы. Вероятность того, что каждая из проб окажется «пустой» равна 0,05.

Определить вероятность того, что:

1) все пробы будут содержать полезное ископаемое;

2) одна из проб окажется «пустой»;

3) две пробы будут «пустыми»;

4) три пробы окажутся «пустыми»;

5) все пробы окажутся «пустыми».

Представить закон распределения в табличной форме.

Решение.

Поскольку события (отбор проб наугад) являются независимыми, вероятности этих событий равны друг другу, то можно применить биномиальный закон распределения и найти искомые вероятности по формуле Бернулли.

По условию задачи n = 4, р = 0,05, q = 1 – p = 0,95.

Контроль: .

Небольшое отступление от единицы объясняется округлением результатов.

Представим полученное биномиальное распределение в табличной форме.

Таблица 1.25

Биномиальный закон распределения (для примера 1.32)

х	0	1	2	3	4
р	0,81451	0,17148	0,01354	0,00047	0,00001

1.6.7. Распределение Пуассона

Распределение Пуассона используется в тех случаях, когда вероятность наступления какого-либо события является малой величиной. Нормальный закон распределения не является эффективным при значениях вероятности, близкой к нулю или близкой к единице.

Закон Пуассона применим как для маловероятных событий, так и для событий, протекающих с большой, весьма близкой к единице вероятностью. Но в последнем случае закон Пуассона применяют по отношению к противоположным событиям, вероятность которых – малая величина, т.е. для событий, вероятность которых определяется выражением (1.125).

Закон Пуассона выражается формулой

, (1.126)

где (значение n задано, постоянное число; k принимает только положительные целочисленные значения; k ≤ n).

Если требуется вычислить вероятность попадания числа k в интервал от а₁ до а₂, то необходимо вычислить сумму

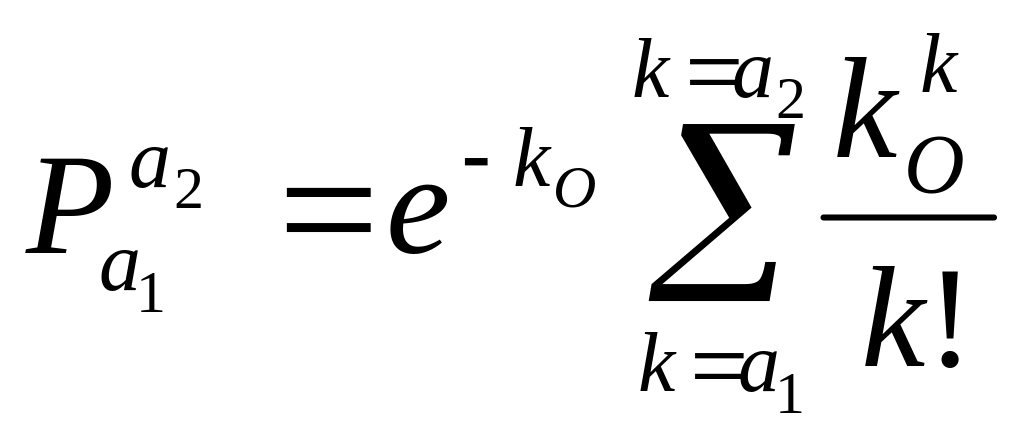. (1.127)

При а₁ = 0 а₂ = а, тогда

. (1.128)

Математическое ожидание и дисперсия для распределения Пуассона M(X) = D = np. Стандартное отклонение .

Пример. 1.23. На автоматическую сейсмостанцию, установленную в горной выработке, за один час поступает 15 сигналов. Найти вероятность того, что в данную минуту станция зарегистрирует: один сигнал; два сигнала; три сигнала.

Решение.

В среднем за одну минуту станция регистрирует k_O = 15 : 60 = 0,25 сигнала. Необходимо найти Р – вероятность поступлении в минуту одного сигнала, двух сигналов, трех сигналов.

По формуле Пуассона находим:

; ; .

Как видно из результатов расчета – вероятность изменяется практически на порядок при последовательном увеличении числа принимаемых сигналов в минуту.

Использование: если, например, при вероятности 0,00203 станция зарегистрировала три, а то и четыре сигнала в минуту, то это говорит об опасности ведения горных работ в данной выработке. Да и увеличение частоты прихода сигналов до одного в минуту также говорит о неблагоприятной обстановке в горной выработке, поскольку вероятность такого события сравнительно малая, чуть меньше 20%.