2.2.3. Оценка эмпирического значения дисперсии

Из теории математической статистики известно, что стандарт дисперсии, если случайная величина распределена по нормальному закону, определяется по приближенной формуле:

, (2.9)

где D = σ² вычисляется с использованием формул (2.5) или (2.6) в зависимости от объема выборки.

При n < 20 используют случайную величину

, (2.10)

которая имеет χ²-распределение.

Преобразуем выражение (2.10) для D':

. (2.11)

В этом случае для построения доверительного интервала пользуются таблицей приложения 4.

Последовательность действий при построении доверительного интервала для дисперсии при n < 20:

- вычисляют значение уровня значимости α = (1 – β), где β – доверительная вероятность;

- из таблицы приложения --- выбирают значения χ₁² и χ₂², соответствующие вероятностям Р₁ = α/2 и Р₂ = 1 - α/2 и числу степеней свободы ν = (n – 1);

- вычисляют доверительные границы

и . (2.12)

Пример 2.3. Для доверительной вероятности 0,95 найти доверительный интервал для дисперсии D = 0,32 и стандарта σ = 0,57, полученных при обработке данных выборки объемом n = 14.

Для сопоставления использовать: а) нормальный закон распределения; б) χ²-распределение.

Решение.

Для нормального закона распределения для доверительной вероятности 0,95 (уровня значимости 0,05) и числа степеней свободы ν = 13 по таблице приложения 10 находим t = 2,16.

Значение стандарта дисперсии .

Отсюда следует, что доверительные границы для дисперсии , доверительные границы для стандарта .

Для χ²-распределения вычисляем вероятности Р₁ = 0,05:2 = 0,025 и Р₂ = 1 – 0,025 = =0,975.

По таблице приложения 4 для числа степеней свободы ν = 13 и полученных значений вероятностей 0,025 и 0,975 интерполированием находим: χ₁² = 24,98 и χ₂² = 4,95.

По формуле (2.12) вычисляем:

, ;

, .

Какие можно сделать выводы?

Во-первых, получены довольно существенные различия при использовании нормального закона распределения и при использовании χ²-распределения.

Во-вторых, доверительные интервалы во втором случае получились несимметричными в силу несимметричности χ²-распределения:

;

2.2.4. Сравнение средних двух или нескольких выборок

Часто приходится решать задачу сравнения средних нескольких, в частности, двух выборочных совокупностей. При этом решается вопрос о том, значимо или незначимо расхождение между полученными средними значениями (точечными оценками) при заданном уровне доверительной вероятности. Если расхождения значимы, то это говорит о неслучайных влияниях или условия проведения эксперимента либо о том, что исследуемые выборки могут принадлежать разням генеральным совокупностям. Если расхождения случайные, то принимают гипотезу о равенстве средних.

Указанная задача может быть решена как в случае известной дисперсии генеральной совокупности, так и в случае, когда дисперсия неизвестна или определено только приближенное ее значение.

Предположим, что у нас имеется несколько выборок большого объема N_i с известным математическим ожиданием X_i и стандартом Σ_i . Каждая из больших выборок подчиняется нормальному закону распределения. Из каждой из указанных больших выборок отобраны выборки объемами n_i << N_i . Для каждой из полученных выборок определнны средние х_oi и дисперсии D_i (стандарты σ_i).

Предположим, что дисперсии генеральных совокупностей известны.

В этом случае для двух, например, любых выборок разности подчиняются нормальному закону распределения с математическим ожиданием

M(d) = k (2.13)

и дисперсией

. (2.14)

Нормированная разность

(2.15)

также подчиняется нормальному закону распределения с математическим ожиданием, равным нулю и дисперсией D(z) = 1.

Задаваясь вероятностью (где β – доверительная вероятность) по таблице приложения 11 находят статистику Z, а также значение z , для которых выполняется условие

, (2.16)

соответствующее принятию гипотезы о равенстве средних.

Пример 2.4. Выполнить попарное сравнение средних трех выборок (первую со второй и первую с третьей), представленных в табл. 2.2, по уровню доверительной вероятности 0,95.

Дисперсии генеральных совокупностей, из которых были отобраны выборки, соответственно равны σ₁² = 21, σ₂² = 15, σ₃² = 19.

Таблица 2.2

К примеру 2.4 (исходные данные)

№№	ni	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	хoi
1	17	131	127	125	120	133	130	128	127	136	132	129	132	119	121	136	125	133	128,5
2	14	132	126	134	128	129	135	124	122	129	125	127	124	122	122				127,1
3	12	131	136	129	123	135	130	132	131	134	129	128	137						131,3

Решение.

Результаты расчетов приведены в табл. 2.3.

Таблица 2.3

К примеру 2.4 (результаты расчетов)

z-тест для двух выборок	Выборка 1	Выборка 2	Выборка 3
Средние (xoi)	128,5	127,1	131,3
Дисперсия (σi^2)	21	15	19
Дисперсия разностей (D(d))		2,31	2,82
Объем выборки (ni)	17	14	12
Гипотетическая разность средних		k1-2 = 0	k1-3 = 0
Значение параметра z		0,92	1,67
Вероятность условия (2.16)		0,179	0,048
Критическое значение параметра z (zкр)		1,65	1,65

Вычисляем по формуле (2.14) дисперсии разностей:

; .

Вычисляем значение параметра z:

; .

По таблице приложения 11 интерполированием для z_1-2 = 0,92 и z_1-3 = 1,67 находим соответствующие вероятности Р_1-2 = 0,179 и Р_1-3 = 0,048.

Критическое значение z_кр = 1,65 находим по той же таблице по уровню значимости 0,05.

Выводы.

1. Поскольку z_1-2 < z_кр, то можно принять гипотезу о равенстве средних 1-й и 2-й выборок.

2. Для второй пары выборок (1-й и 3-й) значение z_1-3 получилось немного больше критического значения. В этом случае с некоторым допущением и может быть принята гипотеза о равенстве средних 1-й и 3-й выборок, но целесообразно предварительно отвергнуть данную гипотезу и провести исследование данных выборок на их подобие другими способами.

В том случае, когда дисперсии генеральных совокупностей неизвестны, то в качестве выборочной оценки принимают оценку (2.14), т.е.

, (2.17)

значение статистики t (статистики Стьюдента) определяют по формуле (2.15)

(2.18)

с вычислением числа степеней свободы по формуле

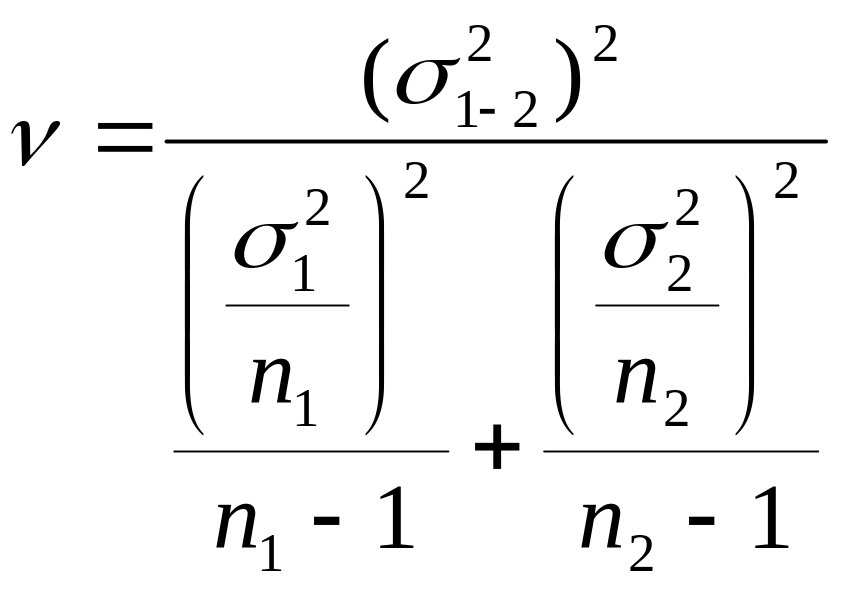. (2.19)

Число степеней свободы округляют до ближайшего целого числа.

Значения дисперсий в формуле (2.17) вычисляют по фактическим данным выборочных совокупностей.

Для вычислений используется таблица приложения 10.

Пример 2.5. Для выборок, приведенных в табл. 2.2 (пример 2.4), выполнить сравнение средних для доверительной вероятности 0,95, если дисперсии генеральных совокупностей неизвестны. Выполнить сравнение средних попарно выборок 1 и 2 и выборок 1 и 3, используя t-тест.

Решение.

Результаты вычислений представлены в табл. 2.4.

Таблица 2.4

К примеру 2.5

t-тест для двух выборок	Выборка 1	Выборка 2	Выборка 3
Средние (xoi)	128,5	127,1	131,3
Объем выборки (ni)	17	14	12
Дисперсия (σi^2)	27,1	18,8	15,3
Дисперсия разностей (D(d))		2,94	2,87
Стандарты разностей σ(d)		1,71	1,69
Гипотетическая разность средних		k1-2 = 0	k1-3 = 0
Значение параметра t		0,82	1,66
Число степеней свободы ν		29	27
Критическое значение параметра t (tкр)		2,054	2,052

По формуле (2.5) находим приближенные значения стандартов и соответствующих дисперсий: σ₁² = 27,1 ; σ₂² = 18,8 ; σ₃² = 15,3 .

По формуле (2.17) находим значения дисперсий разностей для сравниваемых пар:

, ; , .

Вычисляем число степеней свободы для каждой из пар выборок по формуле (2.19):

; .

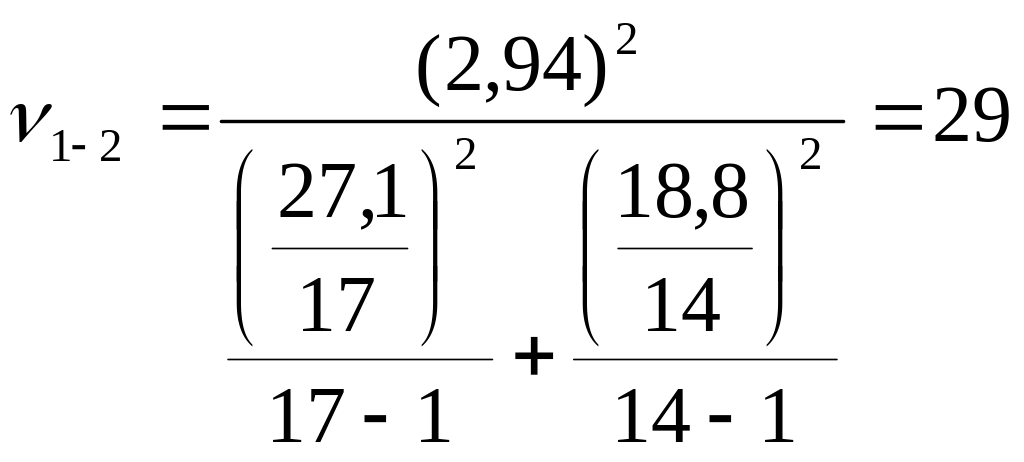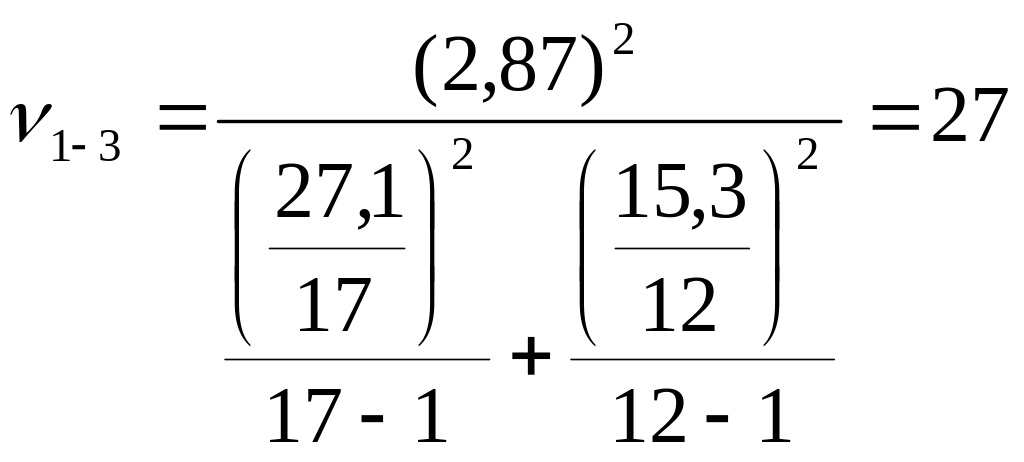По таблице приложения 10 для уровня значимости 0,05 и полученным значениям степеней свободы интерполированием получаем критические значения параметра t: t_1-2 = 2,054; t_1-3 = 2,052.

Вывод. Поскольку значение параметра t для обеих пар выборок не превышают критического значения, то принимаем гипотезу о равенстве средних выборок 1 и 2 и выборок 1 и 3.