3.2.2. Средние квадратические погрешности функций измеренных величин

В п. 3.2.1 рассмотрены средние квадратические погрешности непосредственно измеренных величин. Чаще всего сами непосредственно измеренные величины используются в различных формулах, результатом вычисления по которым являются косвенные величины. Например, площадь прямоугольника, как косвенная величина, может быть определена как произведение сторон прямоугольника, полученных при измерениях непосредственно. Оценку точности площади в этом случае необходимо производить с учетом погрешностей в измерениях его сторон.

Предположим, что имеется некоторая функция F аргументов х₁ , х₂ , … , х_n:

F = f (x₁, х₂, …, х_n) . (3.12)

Величины х_i известны из непосредственных измерений, а также известны и их средние квадратические погрешности m₁ , m₂ , … , m_n . В этом случае средняя квадратическая погрешность функции определяется по следующей формуле:

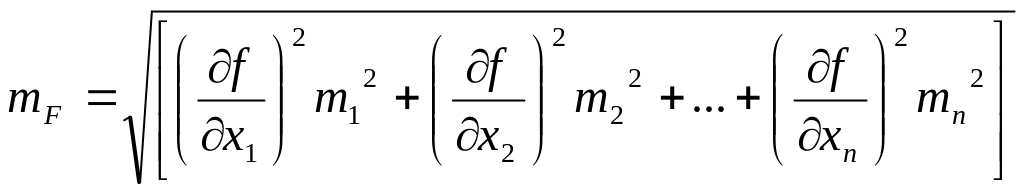, (3.13)

где _–– частная производная функции по аргументу х_i .

Правила определения средних квадратических погрешностей функций следующие.

1. Выполнить последовательно дифференцирование функции отдельно по каждому из аргументов, считая остальные аргументы постоянными числами (коэффициентами).

2. Полученные выражения умножить на средние квадратические погрешности аргументов, по которым производилось дифференцирование функции и возвести полученные выражения каждое отдельно в квадрат.

3. Записать полученные выражения в виде суммы под знаком квадратного корня.

Рассмотрим несколько примеров определения средних квадратических погрешностей функций.

Пример 3.1. Средняя квадратическая погрешность среднего арифметического.

Очевидно, что значение среднего арифметического является функцией суммы измеренных величин х_i . Представим это выражение в виде

х_о = (х₁ + х₂ + … + х_n ) / n . (3.14)

Поскольку 1/n является постоянным коэффициентом, то при почленном дифференцировании и после умножения на m_i и возведения в квадрат пролучим:

, (3.15)

или

. (3.16)

Полагая измерения равноточными, т.е. m₁ = m₂ = ... = m_n = m, выражение (3.16) преобразуем к виду

. (3.17)

То есть средняя квадратическая погрешность среднего арифметического в корень из числа измерений меньше средней квадратической погрешности одного измерения.

С учетом (3.10)

. (3.18)

Очевидно, что, если при увеличении числа измерений значение средней квадратической погрешности одного измерения стремится к предельному значению, отличному от нуля, то значение средней квадратической погрешности среднего арифметического стремится при увеличении числа измерений к нулю, а само среднее арифметическое – к истинному значению.

Пример 3.2. Оценка точности определения объема пирамиды.

Объем пирамиды, основанием которой является прямоугольник, определен по формуле

, (3.19)

где h – высота пирамиды, а и b – стороны основания.

Требуется найти среднюю квадратическую погрешность определения объема пирамиды, вычисленного по формуле (3.19), если известно, что h = 12,34 м, а = 23,46 м, b = 39,63 м и их средние квадратические погрешности равны соответственно m_h = 0,07м, m_a = 0,02 м, m_b = 0,04 м.

Выполняем последовательное дифференцирование по аргументам h, a и b:

• по аргументу h: ;

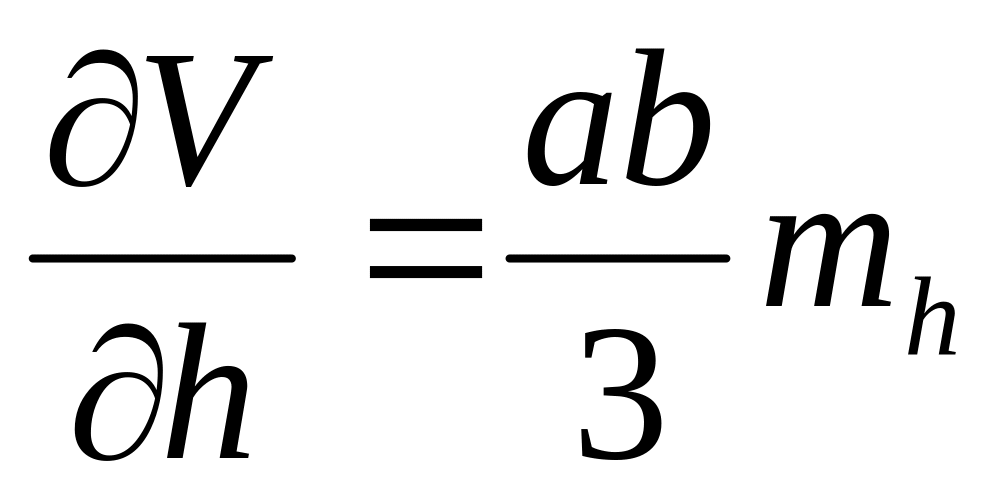• по аргументу а: ;

• по аргументу b: .

Возводим в квадрат полученные части и записываем в виде суммы в подкоренном выражении:

(3.20)

Формулу (3.19) можно преобразовать к следующему виду. Разделим правую и левую части соответственно на ( h a b) и V, получим

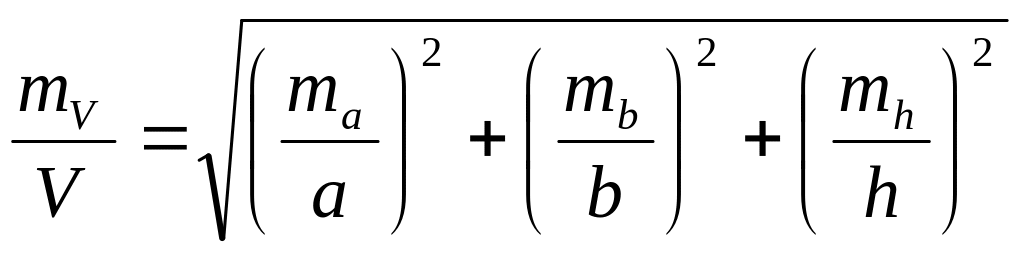(3.21)

или

. (3.22)

где δ - относительные средние квадратические погрешности аргументов и функции.

Выполним вычисления по формуле (3.20).

Значение V = (23,46 ∙ 39,63 ∙12,34) : 3 = 1274,75 м³.∙

Относительная средняя квадратическая погрешность определения объема равна δ_V = 7,42 /1274,75 = 0,00582 = .

Выполним проверку значения δ_V по формуле (3.22).

Относительные средние квадратические погрешности аргументов равны:

δ_h = 0,07 : 12,34 = 0,00567, δ_a = 0,02 : 23,46 = 0,00085, δ_b = 0,04 : 39,63 = 0,00101.

После подстановки в формулу (3.22) получим δ_V = 0,00582, что совпадает с предыдущим результатом.

Пример 3.3. Тригонометрические функции.

Сторона а треугольника определена по теореме синусов по значению стороны b и двум углам треугольника А и В:

Известно: b = 140,12 м (δ_b = 1 : 2000; m_b = 140,12 : 2000 = 0,07 м), А = 73^о18,8' (m_А = 0,4'), В = 63^о 05,6' (m_В = 0,3').

Необходимо определить среднюю квадратическую погрешность стороны а.

Вычисление стороны а производится по формуле

. (3.23)

Запишем члены подкоренного выражения для средней квадратической погрешности параметра а:

• для аргумента b: (m_b sin A / sin B )²;

• для аргумента А: (b m_A cos A /r' sin B )²;

где r' = 3438¢ (число минут в радиане; для выражения угловой меры средней квадратической погрешности угла в радианную меру);

• для аргумента В: (b m_B sin A cos B / r sin² B)².

Следовательно,

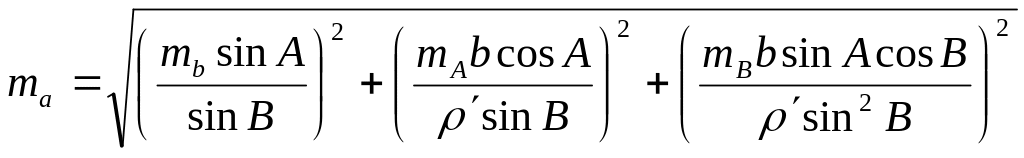. (3.24)

После подстановки значений аргументов получим: m_а= 0,096 м.

Как показывают данные расчетов, большее влияние на погрешность стороны а оказывает первый в записи член, определяемый погрешностью аргумента b. Двумя другими членами общего выражения для погрешности стороны а можно пренебречь. Однако следует иметь в виду и то, что малое влияние второго и третьего членов подкоренного выражения обусловлено сравнительно малой погрешностью измерения углов по сравнению с погрешностью измерения стороны b. Следовательно, в рассмотренном случае углы можно измерять с большей погрешностью, чем это указано в условии задачи.

Значение стороны а, вычисленное по формуле (3.23), равно 189,81 м.

Относительная погрешность определения стороны а будет равна

δ_а = m_a / а = 0,096 / 189,81 = 1 / 1977,

т.е. практически она равна относительной погрешности измерения стороны b.