2.5. Регрессионный анализ
Первоначально понятие регрессия было использовано в биологии для описания процессов изменения биологических объектов. Затем оно было применено К.Паскалем в математической статистике, используя общий его смысл – упрощение.
Регрессионный анализ – это метод моделирования измеряемых данных и метод исследования их свойств. Парметры модели подбираются так, что модель наилучшим образом описывает закономерные связи между переменными.
В математической статистике регрессия характеризует зависимость математического ожидания случайной величины от одной или нескольких случайных величин (свободных переменных). При этом, в основном, математическое ожидание не является, например, математическим ожиданием всей выборочной совокупности, а в качестве него могут выступать и выступают средние значения параметра в классах вариационного ряда.
Известно, что между различными измеряемыми параметрами существуют такие связи, как корреляционная, функциональная и стохастическая.
Корреляционная связь или корреляционная зависимость характеризуется, как это было установлено в п. 2.4, теснотой связи. Кроме этого корреляционная зависимость предусматривает и установление формы связи.
Если каждому значению одной переменной ставится вполне определенное значение другой переменной, то такая их взаимосвязь называется функциональной зависимостью.
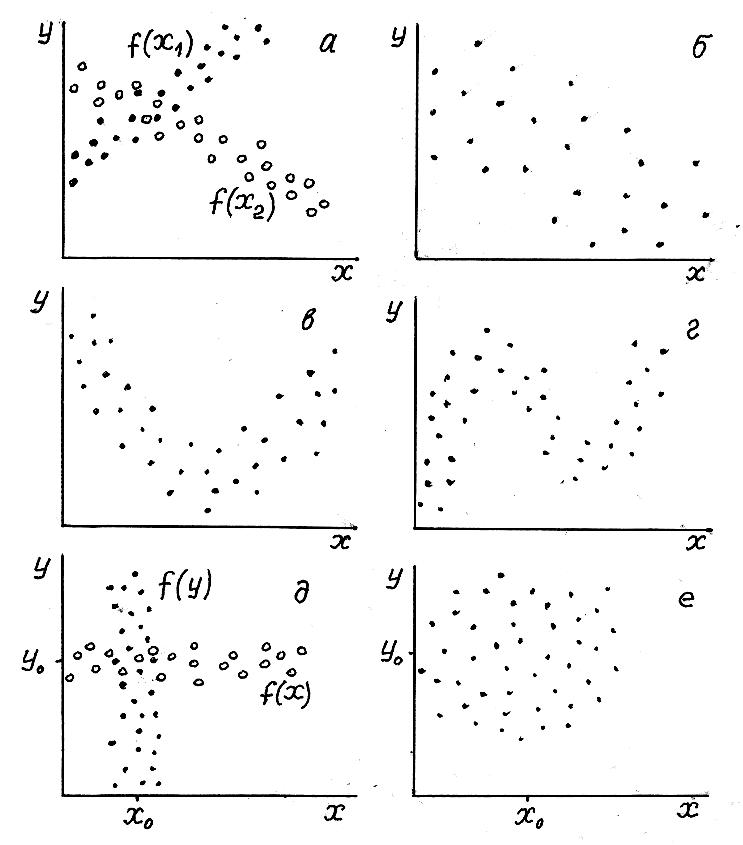
Рис. 2.1. Связи между случайными величинами
а – сравнительно четкая линейная зависимость; б – слабая линейная зависимость;
в – нелинейная зависимость сравнительно простого вида;
г – нелинейная зависимость сложного вида; д – связь между случайными величинами отсутствует; е – связь между случайными величинами не определяется
К достаточно сложной связи относится стохастическая связь, при которой случайная величина реагирует на изменение другой случайной величины изменением своего закона распределения. Это вид причинной зависимости, которая проявляется не в каждом отдельном случае, а в среднем, при большом числе измерений. Эта связь отличается приближенностью и неопределенностью. Стохастические связи невозможно свести к функциональной зависимости.
При исследовании вариационных рядов, случайных величин используют т.н. линейную регрессию, нелинейную регрессию и множественную регрессию.
Линейная регрессия определяет линейную зависимость между случайными величинами, определяемую формулой (1.77). Нелинейная регрессия может быть представлена, в частности зависимостями, представляемыми выражениями (1.82), (1.89), (1.96) и др.
На рис. 2.1 представлены некоторые виды связей между случайными величинами, представленные в виде т.н. «роев».
На рис. 2.1а показана сравнительно четкая зависимость между случайными величинами х и у. Положительный коэффициент корреляции для функции f(x1) и отрицательный – для функции f(x2).
Линейная зависимость прослеживается и на рис. 2.1б (отрицательный коэффициент корреляции), но эта зависимость выражена сравнительно слабее, чем рассмотренная выше.
Нелинейные зависимости представлены на рис. 2.1в и 2.1г. На рис. 2.1в возможно предположение о зависимости параболического вида, на рис. 2.1г нелинейная зависимость сложная, выявление такой связи представляет уже некоторые трудности.
На рис. 2.1д показаны два вида возможной связи (принято определять, что связь такого вида между случайными величинами является не закономерной). Первая – при любых значениях случайной величины х случайная величина у равна своему математическому ожиданию (постоянной величине). В этом случае график зависимости параллелен оси Ох. Вторая закономерность – обратная: для одного и того же постоянного значения случайной величины (изменяющейся в весьма малых пределах) вторая случайная величина может принимать любые значения (в пределах вероятного диапазона ее изменения). В этом случае график параллелен оси Оу.
На рис. 2.1е связь меджу случайными величинами не устанавливается: для любого изменения случайной величины в вероятных пределах ее существования вторая случайная величина может принимать любые значения в вероятных пределах ее существования.