5 Тарау интегралдар

§5.1 Комплекс сандар

Комплекс сандар деп теңдік түсінігі мен арифметикалық амалдар төмендегі 1)-4) ережелермен берілген

түріндегі өрнектерді айтады. Мұндағы х,у-нақты сандар, ал олар z санның сәйкес нақты және жорамал бөліктері деп аталады да x = Rez, y = Jmz арқылы белгіленеді, комплекс сандар теңдігі және арифметикалық амалдар келесі ережелер арқылы енгізіледі:

1) мен 3) –тен і²=-1 теңдігі шығады, і-жорамал бірлік сан.

2) мен 3) теңдіктерден комплекс сандарды қосу және көбейту амалдары нақты сандарды қосу және көбейту амалдардың барлық қасиеттеріне ие, сонымен бipгe комплекс сандарға жасалатын амалдар (і²=-1 ескеріп) алгебрадағы өрнектерге жасалатын амалдар сияқты орындалатынын көреміз.

z = х - iy саны z = х + iy санына түйіндес деп аталады.

-нақты саны z -комплекс санының модулі деп аталады.

теңдігінің орындалатынын көру қиын емес.

Әрбір z = x + iy комплекс санын хОу жазықтығының М(х,у) нүктесімен (-векторымен) бейнелеуге болады ( 26-сурет).

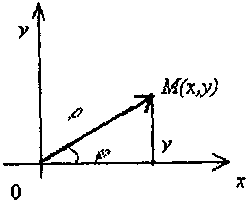
26-сурет

Егер жазықтықта (р,)поляр координаталарын енгізсек, онда

Бұдан

теңдігі шығады. Мұндағы p=|z|, q>- векторы мен Ох өсінің оң бағыты арасындағы бұрыш (радиан өлшемінде).

Бұл бұрыш

символымен белгіленіп z комплекс санының аргументі деп аталады.

Көп мәнді, дәлірек айтқанда, z-әpбip мәніне Argz-тің шексіз көп мәндерді сәйкес келетін функция. Осыған орай = argz, - < argz -аргументтің бас мәні деп те атайды.

z = 0 үшін |0| = 0, ал argO- мағынасы жоқ. argz үшін (z0) келесі теңдіктер орындалады:

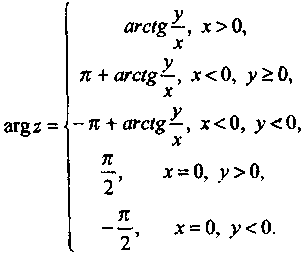
Екі z₁ және z₂ комплекс сандарының теңдігін келесі түрде тұжырымдауға болады: z₁ = z₂ болуы үшін олардың модульдері тең, ал аргументтері тең немесе олардың айырымы 2-ға еселі шамаға тең болуы қажет және жеткілікті. Сонымен,

Анықтама бойынша

функциясы 2-периодты функция:

болғандықтан ) өзгергенде нүктесі радиусі 1-ге тең, центрі z = 0 болатын шеңберді сызады.

теңдіктерінің орындалатынын көруге болады (тексеріңіз).

Кез келген z = х + iy комплекс айнымалысы үшін e^z функциясын келесі тееңдікпен анықтайды:

Бұдан (3)-ті ескеріп

аламыз. Ал (2), (З)-тен

шығады. Мұндағы р = \z\, ал

бұрышы 2k, k = О,1, ... дейінгі дәлдікпен анықталады.

(2) мен (6) - z комплекс санының сәйкес тригонометриялық және көрсеткіштік түрлері деп аталады, ал z = х+іу -өзін комплекс санның алгебралық түрі деп атайды.

§5.2. n - ші дәрежелі көпмүшеліктер

1.п - ші дәрежелі нақты көпмүшеліктер.

Егер

көпмүшелігінің a_k коэффициенттері тек нақты сандар болса, онда оны нақты n - ші дәрежелі көпмүшелік деп атайды. Өйткені, бұл жағдайда (l)-гі z = х нақты айнымалы болса, көпмүшелік нақты мәндерге ие болады. Әрине, комплекс айнымалы z үшін көпмүшелік комплекс мәндер қабылдайды.

Теорема. Егер z₀ = комплекс саны Q_n нақты көпмүшеліктің түбірі болса, онда оған түйіндес z₀=комплекс саны да осы көпмүшеліктің түбipi болады.

Ескерту. Егер z₀ =Q_n -нақты көпмүшеліктің S-еселі түбірі болса, онда z₀ = саны да Q_n -нак,ты көпмүшеліктің S-еселі түбірі болады, сондықтан

немесе

теңдігі орындалады.

Егер

деп алсақ, онда (2) теңдікті келесі түрде жаза аламыз

с₁,...с_г нақты сандары Q_n көпмүшелігінің сәйкес і₁,...i_r, еселі түбірлері, ал комплекс сандары оның сәйкесj₁,--j_s еселі түбірлері болса (і₁,+... + i₂ + 2(j₁ +... + j_s) = n) онда бас коэффициенті а_n 0 тең n-ші дәрежелі Q_n нақты көпмүшелігін сызықтық және квадрат көбейткіштеріне келесі түрде жіктеуге болады.

Мұндағы квадрат көбейткіштердің әpбipeyi үшін

орындалады, яғни

2. Рационал функция және оны ең қарапайым бөлшектер қосындысына жіктеу. Екі алгебралық көпмүшеліктердің қатынасы

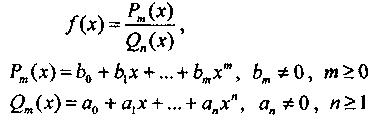
рационал функция немесе рационал бөлшек деп аталады.

Р_m және Q_n-нақты көпмүшеліктер және х-нақты айнымалы деп есептейміз.

(мұндағы а,р,q,А,В-нақты сандар; түріндегі бөлшектер ең қарапайым бөлшектер деп аталады.

Егер m>n болса, онда бөлу арқылы f(x) функциясын оның бүтін бөлігі мен дұрыс бөлшек деп аталатын

m ₁< n бөлшектің қосындысы түрінде жаза аламыз:

f(x) = көпмүшелік + m ₁< n.

Енді (5) бөлшекті дұрыс (m < n) деп алып, оны ең қарапайым (6) бөлшектердің қосындысына жіктеу меселесін қарастырайық.

Теорема. m < n бөлшегінің бөлімі (4) теңдік түрінде жіктелінсін:

Онда ол бөлшекті жалғыз түрде келесі қосындыға жіктеуге болады:

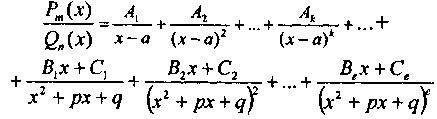
Мұндағы А₁,В₁,C₁-тұрақты сандар.

Қорытынды. № 49-50 лекциялардан кейін студенттер комплекс санмен танысып онымен амалдар жасай алады және күрделі рационал бөлшекті жай рационал бөлшектердің қосындысы ретінде жіктеуді үйренеді.

№ 51-52 лекциялар. Анықталмаған интеграл ұғымы оның қасиеттері және таблицалық интегралды пайдаланып интегралдарды есептеу жолдары қарастырылады.