§ 5.4. Интегралдау әдістері

1. Ауыстыру (айнымалыны алмастыру) әдісі.

Интегралдық есептеулерде айнымалы ауыстыру формуласы ерекше орын алады.

Теорема. (интегралдау формулаларының инварианттылығы). u= φ(х) кез келген дифференциалданатын функция болсын. Егер

онда

(1)

немесе

Егер x = φ(t) қандай да бip аралықта үзіліссіз дифференциалданатын функция болса, онда

(2)

(2) айнымалы ауыстыруын жасағанда, ψ(t) мен f(x) функцияларының анықталу аймақтары D_t мен D_x арасында өзара бip мәнді сәйкестік (оны D_t ↔ D_x деп бейнелейді) болатындай және x = ψ(t) функциясы D_x аймағындағы мәндерін түгел қабылдайтындай болуы тиіс.

2. Бөліктеп интегралдау. Егер и(х) және v(x) функциялары үзіліссіз дифференциалданатын функциялар болса, онда

(3)

немесе (басқа түрде)

(4)

Бұл формулалардағы С-тұрақтысын (бізге белгілі себептерге байланысты) жазбайды.

(3) немесе (4) формулаларын қолданып есептеу –бөліктеп интегралдау әдісі деп аталады.

Бұл әдісті формуланың оң жағындағы интеграл сол жағындағы берілген интегралға қарағанда қарапайымдау болған жағдайда қолданған жөн. Және де и үшін туындысы ықшамдау болатын көбейткішті алады.

Қорытынды. № 53-54 лекциялардан кейін анықталған интегралды алмастыру және бөліктеп интегралдау тәсілдерімен меңгеруді және есептер шығарып машықтанады.

№ 55-56 лекциялар. Рационал бөлшектерді, тригонометриялық өрнектер және иррационал өрнектерді интегралдау тәсілдері қарастырылады

§5.5. Рационал белшектерді интегралдау.

Келесі рационал бөлшекті немесе рационал функцияны

(1)

интегралдау жолдарын көрсетейік.

Мұндағы - нақты көпмүшеліктер, ал х-нақты айнымалы деп есептейміз.

Егер m≥n болса (бүл жағдайда (1)-бұрыс бөлшек деп аталады), онда алымын бөліміне «бұрыштап» бөлу арқылы келесі қосындыны аламыз

(2)

мұндағы (m-n) –ші, ал -m₁- ші дәрежелі көпмүшеліктер және де m₁< п.

Егер алымының дәрежесі бөлімінің дәрежесінен кіші болса, онда рационал бөлшек дұрыс бөлшек деп аталады.

Сонымен, (2)-дегі m₁< n -дұрыс бөлшек.

Көпмүшелікті интегралдау қиын емес, сондықтан рационал бөлшекті интегралдау қиындықтары дүрыс бөлшекті интегралдауда жатыр.

Дұрыс бөлшекті интегралдаудың негізгі тәсілі - дұрыс бөлшекті қарапайым бөлшектердің қосындысына жіктеу (§2.2. параграфты қараңыз).

Қарапайым бөлшектерді

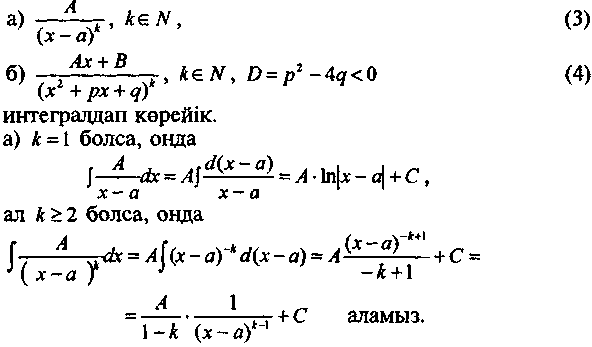
б) (4)-түрдегі қарапайым бөлшекті k = 1 үшін интегралдайық.

Сонымен, k = 1 болсын. Онда

§5.6. Кейбір иррационал өрнектерді интегралдау

Рационал емес элементар функциялардыц интегралдарын айнымалыны алмастыру арқылы рационал функцияның интегралына келтіруге болатын яғни, интегралды рационалдауға болатын жағдайларды қарастырайық.

R(х,у)- өз аргументтері х пен у-тің рационал функциясы болсын, ол R(х,у)-өрнегін алу үшін х пен у-ке тек арифметикалық амалдар қолданылады деген сөз.

I. Есептеу керек:

- мұндағы a,b,c,d - тұрақты сандар, m-натурал сан, ad-bc≠0. Интеграл астындағы функция сызықты бөлшек иррационалдық деп аталады.

Бұл интеграл айнымалы ауыстыруы арқылы рационалданады. Шынында да,

өрнектері рационал функциялар. Ал рационал функция­лардың рационал функциясы — рационал функция. ∆

П. Есептеу керек: мұндағы а,b,с – тұрақты сандар. Интеграл астындағы функция квадрат иррационалдық деп аталады.

Егер ах²+bх + с квадрат үшмүшелігінің x₁,x₂ – нақты түбірлері болса, онда ах² + bх + с = а(х – х₁)(х -х₂) және

аламыз, яғни I-түрдегі сызықты-бөлшек иррационалдыққа келеміз.

Сондықтан, D = b² - 4ас < 0 деп алайық: егер а > 0 болса, онда интегралды Эйлер ауыстыруы:

(Э.а)

арқылы рационалдауға болады. Өйткені, (Э.а)-нан

шығады. Бұны (Э.а)-оң жағына қойсақ

-рационал функция аламыз.

Ескертпе. Егер а<0, ал с> 0 (ах²+bх + с ≥ 0) болса, онда келесі ауыстыруды жасауға болады:

Ескертпе. - түріндегі интегралдарды басқа да ауыстырулар арқылы рационалдауға болады. Мысалы, бұларды сәйкес

тригонометриялық ауыстырулармен рационалдай аламыз.

Біз осыған дейін алгебралық (рационал және иррацио­нал) функциялардың интегралдарын қарастырып келдік. Енді алгебралық емес функциялардың, алдымен тригонометриялық функциялардың интегралдарын қарастырамыз.