§ 5.7. Тригонометриялык функцияларды интегралдау

(1)

түріндегі интегралды табайық. Бұл интеграл

(2)

ауыстыруы арқылы әрқашанда рационал функцияның инте­гралына келеді. Расында да,

(3)

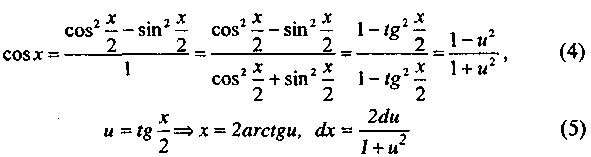
болады, яғни sinx, cosx, dx - рационал функциялар арқылы өрнектеледі. Ал рационал функциялардың рационал функциясы рационал функция болатыны белгілі.

Жоғарыда атап айтқанымыздай u ауыстыруы (1) түрдегі интегралды әрқашанда элементар функция арқылы өрнектей алатындықтан, оны универсал (әмбебап) ауыстыруы деп атайды. Бірақ универсал ауыстыруы «күшті» әдіс болу себебінен көп жағдайларда керекті түрлендірулерді қысқа және қарапайым етіп жасау мағынасында ең жақсы әдіс бола бермейді.

Егер, мысалы, sinx пен cosx R функциясының өрнегіне жұп дәрежелерімен кipiп тұрса, онда

u = tgx

ауыстыруы мақсатка тезірек жеткізеді.

∫R(tgx)dx туріндегі интегралда u = tgx ауыстыруы арқылы алынады.

Енді (1) турдегі интегралдардың дербес жағдайы болатын

интегралын есептеп көрейік.

а) Егер m немесе n санының ең болмағанда бipeyi тақ оң сан болса, онда тақ дәрежеден бірінші дәрежелі бip көбейткіш бөліп, қалған жұп дәрежені cos²x + sin²x = 1 формуласының жәрдемімен толықтауыш функция арқылы өрнектеп кестелік интегралға келуге болады.

б) Егер m мен n тepic емес бүтін жұп сандар болса, онда дәрежені төмендету формулалары қолданылады:

в) Егер m + n = -2k, kN,яғни m +nп теріс таңбалы бүтін жұп сан болса, онда u = tgx немесе u = ctgx ауыстыруын жасаған жөн.

түріндегі интегралдар келесі көбейтіндіні қосындыға түрлендіру формулалары арқылы кестелік интегралдарға келеді:

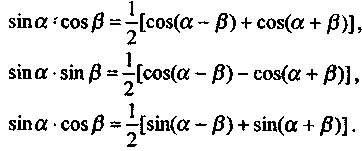
Қорытынды. № 55-56 лекциялардан кейін рационал бөлшектен, иррационал өрнектердің кейбіреуінен және тригонометриялық өрнектерден анықталмаған интеграл есептей алатын болады.

№ 57-58 лекциялар. Анықталған интеграл ұғымы, оның қасиеттері және оны есептеу тәсілдері.

§ 5.8. Анықталган интеграл ұғымына әкелетін есептер.

Анықталған интеграл анықтамасы, қасиеттері

1. Геометриялық және физикалық есептер. Анықталған

интеграл анықтамасы.

I есеп. [а,b] кесіндісінде (а мен b шектелген сандар) үзіліссіз f(x)>0 функция­сы

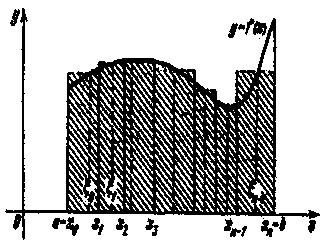
28-сурет

берілсін. y = f(x) қисығы, Ox өci және х = а мен х = b түзулерімен шенелген фигураның (28-сурет) S ауданын анықтау керек.

Аталған фигураны қисық сызықты трапеция деп те атайды.

I есепті шығару үшін келесі амалды орындаймыз: а) [а,b] кесінді кез келген

а = х₀ < х₁ < х₂ <... < х_n = b нүктелерімен п бөлікке бөлеміз:

және y = f(x) қисығының (х_j f(х_j)), j = 0,1,...,n-1 нүктелерінің f(x_j) ординаталарын тұрғызамыз;

б) әрбір бөлікше кесінділерден кез келген нүктесін

аламыз және осы нүкгелердегі функция мәндерін тауып келесі қосындыны құоамыз

Бұл - f(x) функциясының [а,b] кесіндідегі интегралдық қосындысы деп аталады. Оның әрбір

қосылғышы — табаны [x_J+l, x_J] және биіктігі тең тік төртбүрыш ауданына тең, ал S_n қосындысы қисықсызықты трапеция ауданын қандай да бip дәлдікпен жуықтайды:

Бұл жуық теңдік дәлірек болуы үшін барлық [x_J,x_J+l] j=0,l,...,n-l бөлікше кесінділерді мейлінше ұсақтай түсу керек екені түсінікті;

в) Ең үлкен бөлікше кесіндіні нөлге ұмтылдырамыз (әрине, мұнда барлық ∆х_j нөлге үмтылады).

Егер осыдан S_n-шамасы [а,b] кесіндісін бөлу тәсіліне және әрбір бөлікше кесінділерден алынған нүктелерін таңдау тәсілдеріне тәуелсіз S анықталған шегіне ұмтылса, онда S шамасы қисықсызықты трапеция ауданы деп аталады. Сонымен,

(1)

II есеп. х-өсіндегі [а,b] кесіндіде жатқан сызықтық, біртексіз стержень (желі) берілсін. Оның массасының үлестіру тығыздығы ρ(х) –үзіліссіз функция болсын. Осы стерженнің массасын анықтау керек.

а) Стерженді кез келген a=x₀<x₁<...,<x_n=b нүктелерімен п бөлікке бөліктейміз:

б) Әрбір [x_J,x_J+l] бөліктен кез келген нүктесін аламыз:

және келесі интегралдық қосындыны құраймыз

[x_J,x_J+l] –аралығында ρ(х) функциясының өзгеруі шамалы ғана болатындықтан, стерженнің [x_J,x_J+l] кесіндісіне сәйкес келетін бөлігінің массасы жуықтап тең болғандықтан М_n қосынды бүкіл стерженнің массасын жуықтайды;

в) Стерженнің массасының дел мәнән ең үлкен бөлікше кесіндіні нөлге ұмтылдыра отырып М_n нтегралдық қосындысының шегіне өту арқылы аламыз

(2)

Осы сияқты f күшінің әсерінен дененің түзу сызықпен [а,b] аралығында қозғалысының А жұмысын анықтауға болады:

Тағы да басқа көптеген физикалық есептерді осы сияқты шешуге болады.

Бұл есептер бізді [а,b] кесіндісіне берілген, тегі әр түрлі функцияларға жасалатын бip ғана математикалық амалға алып келеді. Бұл амал — функцияны кесіндіде интегралдау деп, ал оның нәтижесі — функцияның кесіндідегі анықталған интегралы деп аталады.

Аныктама. [а,b] кесіндісінде y=f(x) функциясы берілсін.

а) [а,b] кесіндісін кез келген

нүктелерімен [x_J,x_J+l] j=0,l,...,n-l бөліктерге бөлеміз (оны R бөліктеуі деп атайық);

б) Әpбip [x_J,x_J+l] бөліктен кез келген нүктелерін алып f функциясының R –бөліктеуіне сәйкес интегралдық қосындысы деп аталатын

қосындыны құрамыз;

в) mах ∆х_j→0 ұмтылдырып интегралдың қосындының шегін аламыз

Егер бұл шек бар болса, онда ол f функциясының [а,b] кесіндісіндегі анықталған интегралы деп аталады да келесі түрде белгіленеді

(3)

а мен b сандары анықталған интегралдың, сәйкес, төменгі және жоғары шегі деп аталады.

Анықтамада айтылған [а,b] кесіндісін бөліктеу тәсілі де, нүктесін алу тәсілі де шексіз көп.f функциясының интегралдық қосындысының шегі бар болса, ол осы тәсілдерге тәуелсіз. Басқаша айтқанда, кез келген R-бөліктеу мен - нүктелері үшін алынған шек бip ғана санға тең. Бұл жағдай, әрине,f функциясының сипатына байланысты. Мысалы, f [а,b] – кесіндісіне үзіліссіз болса, онда оның интегралдық қосындысының шегі бар.

Бұл анықтама үзіліссіз функциялар үшін француз математигі Коши және жалпы жағдай үшін неміс математигі Б.Ф. Риман (1826-1866) еңгізген.

(3) шек — Риман интегралы, ал ол шек бар болатын f(x) функциясы Риман мағынасында интегралданатын функция деп аталады.

(1), (2) және (3) теңдіктерден келесі қорытынды жасауға болады:

1) y = f(x)≥0 қисығы Ох - өci және х = а мен х = b түзулерімен шектелген жазық фигура ауданы S f(x)-функция­сының [а, b] кесіндісіндегі анықталған интегралына тең

2) Ох ес1нде орналаскан, үлестіру тығыздығы ρ(х) тең [а,b] біртексіз стерженнің М массасы осы ρ(х) функция­сының [а,b] кесіндісіндегі анықталған интегралына тең

Анықталған интегралды оның анықтамасы арқылы есептеу қиын жұмыс. Сондықтан анықталған интегралды есептеудің басқа тәсілін табу қажет болды. Бұл бағытта ағылшын физигі И.Ньютон (1643-1723) және неміс математигі Г.В.Лейбниц (1646-1716) шешуді жұмыс атқарды. Олар математикалық анализдің маңызды түсініктері - интеграл мен туындыны байланыстыратын теореманы делелдеді. Оның түйіні мынау: егер f(x) [а,b] -де үзіліссіз функция, ал F(x) оның осы кесіндідегі қандай да бip алғашқы функциясы (F'(x) = f(x)) болса, онда (Ньютон-Лейбниц формуласы)

Жоғарыда ескерткеніміздей, егер [а,b] кесіндісіне үзіліссіз функцияның интегралданатын функция болатынын белгілі деп алсақ, онда (4) формуланы оп-оңай дәлелдеуге болады.

Ескертпе. [а,b] - кесіндісінде үзіліссіз немесе монотонды функцияның осы кесіндіде интегралданатын функция болаты­нын дәлелдеуге болады.

Теорема, [а,b] - кесіндісінде шенелмеген функция осы кесіндіде интегралданбайды.

Бірақ функцияның [а,b] кесіндісінде шенелген болуы оның осы кесіндіде интегралдануы үшін жеткіліксіз.