§4.4. Күрделі және айқындалмаған функцияларды дифференциалдау

Күрделі функция туындысы. Толық туынды

(1)

теңдеудегі u мен v тәуелсіз х пен у айнымалыларының функциялары болсын:

(2)

Бұл жағдайда z тәуелсіз х және у айнымалыларының күрделі функциясы болады.

Егер z-тi тікелей х,у арқылы өрнектесек

(3)

аламыз.

F(u,v), φ (х,у), ψ(х,у) функцияларының барлық аргументтері бойынша дербес туындылары үзіліссіз болсын.

(3) - тендеуді пайдаланбай, тек (1) мен (2) тендеулерінен және есептейік.

у-мәнін өзгертпей сақтай отырып, х –аргументіне ∆х-өсімшесін берейік. Онда, (3) бойынша Ф ∆_xФ дербес өсімше, ал u мен v ∆_xv және ∆_xv өсімшелерін алады. Сондықтан, өз кезегінде z = F(u,v) функциясы ∆F(u,v) өсімшесіне ие болады (§2 -ні қараңыз):

∆F(u,v) өсімшесі (З)-теңдік бойынша ∆_xФ тең екенін көрсетеміз. Соңғы теңдіктің барлық мүшелерін ∆_x-ке бөлеміз:

Егер ∆_x→0 ұмтылса, онда

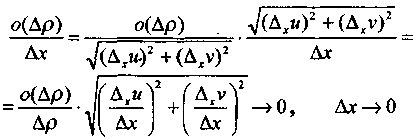
өйткені ∆_x→0 ұмтылса u мен v үзіліссіз болғандықтан,

демек ал

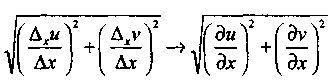
Сондықтан (4) - теңдіктен, ∆_x→0 ұмтылдыра отырып

(5)

аламыз.

х аргументінің мәнін өзгертпей у айнымалысына ∆у өсімшесін берген болсақ, онда дәл жоғарыдағыдай пайымдаулар арқылы

(5')

алған болар едік.

(5) пен (5') формулалар – тәуелсіз аргументтерінің және «аралық» айнымалылардың саны екіден көп функцияларға да осылар сияқты жалпыланады.

Мысалы, аргументтері u,v,...,w болатын z функциясы беріліп ол аргументтер тәуелсіз x,y,...,t айнымалыларының функциялары болсын. Онда

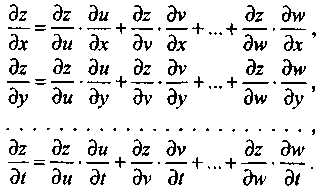
Дербес жағдайда u,v,...,w аргументтері тәуелсіз бip айнымалы х-тің функциялары болса, онда ic жүзінде z тек осы бip х –тің айнымалысының функциясы болады, сондықтан да, туындысын табу туралы сұрак, қоюға болады.

Бұл туынды жоғарыдағы теңдіктердің біріншісі бойынша есептеледі және оны толық туынды деп атайды:

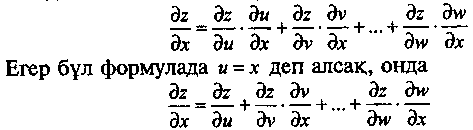(6)

аламыз.

2. Айқындалмай берілген функциялардың туындысы. х –тің қандай да бip y-функциясы

(7)

теңдеуімен айқындалмай берілсін.

Теорема. Координаталары (7) теңдеуді қанағаттандыратын (х,у) нуктесі G аймағында жатсын.

Егер G аймағында F(x,y), F'_x(x,y), F'_y(x,y) функциялары үзіліссіз, ал F'_y(x,y)≠0 болса, онда х-тің у функциясының туындысы бар және ол

түріндегі теңдеуді қарастырайық.

Егер қандай да бip аймақтың әрбір х пен у сандар жұбына (9) теңдеуді қанағаттандыратын z-тің бip немесе бірнеше мәндері сәйкес келсе, онда бұл теңдеу х және у айнымалыларының бip немесе бірнеше z функциясын айқындамай анықтайды.

(9) тендеумен айқындалмай анықталған z функциясының жэнедербес туындыларын табайық.ізделінгендеу тұрақты болып саналады. Сондықтан, (8) формуланы қолданамыз, тек тәуелсіз айнымалы х, ал

функция z болып саналады.

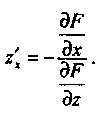
Дәл осылай,

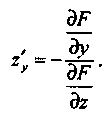
Соны кез келген айнымалы айқындалмаған функциясы үшін де олардың дербес туындылары осылайша анықталады.

§4.5. Бағыт бойынша туынды. Градиент және оның қасиеттері.

Жанама жазыктық және нормаль (тіктем)

1. Бағыт бойынша туынды. D аймағында үзіліссіз және барлық дербес туындылары да үзіліссіз болатын u=f(x,y,z) үш айнымалы функция берілсін. M(x,y,z)Dжәне бағыттаушы косинустары cos α, cosβ, cosγ болатын S векторын қарастырайық (25-сурет).

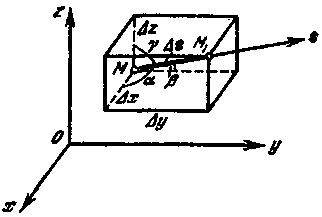
25-сурет

векторында, оның басынан ∆S қашықтықта М1 (х+∆х, у+∆у,z+∆z) нүктесін белгілейміз. Онда

болады да u(x,y,z) функция­сының толық өсімшесін

(1)

түрінде жаза аламыз. Мұнда ε₁, ε₂,ε₃ шамалары ΔS→0 (ұмтылса) нөлге ұмтылады. (1)-нің барлық мүшелерін ΔS -ке бөлейік

(2)

мұнда

болатыны көpiнiп тұр. Сондықтан, (2)-ні келесі түрде жаза аламыз

ΔS→0 ұмтылғандағы қатынасының шегі u = u(x,y,z) функциясының (x,y,z) нүктесіндегі вектор бағыты бойынша туындысы деп аталады да арқылы белгіленеді. (З)-теңдікпен ΔS→0 ұмтылдыра отырып шекке өтсек

(4)

аламыз. Дербес туындьлар, бағыт бойынша туындының дербес жағдайлары. Мысалы,

α = 0, β = γ = π/2, яғни = (1,0,0) болса, онда

аламыз.

2. Градиент. u = f(x,y,z) функциясыныц (x,y,z) нуктесіндегі градиенті деп арқылы белгілінетін

(5)

түріндегі векторды айтады.

(4) формуладан бірлік вектор бағыты бойынша туынды

(6)

яғни, екі вектордың скаляр көбейтіндісі екенін көреміз, олай болса ол градиенттің векторына проекциясы:

Сондықтан, кез келген векторы ушін келесі теңсіздік орындалады

(7)

Егер болса, онда (7)қатыстың теңдік белгісі, тек векторына бағыттас жалгыз = (cosα, cosβ, cosγ) векторы үшін ғана орындалады, ал одан басқа векторлар үшін қатаң теңсіздік орындалады.

Бұл айтылғандардан, u функциясының (x,y,z) нүктедегі градиентін келесі екі қасиетке ие вектор ретінде анықтауға болатынын көреміз:

1) ол вектордың ұзындығы (x,y,z) нуктедегі бағыт бойынша туындының ең үлкен шамасына тең;

2) ол вектордың бағыты туындысы ең үлкен болатын вектормен бағыттас.

3. Жанама жазықтық және нормаль (тіктем). S беті

теңдеуімен айқын емес түрде берілсін. нүктесінің қандай бip маңайындаF функциясының бip мезгілде нөлге тең емес, үзіліссіз дербес туындылары бар және F(P₀) = F(x₀,y₀,z₀) = 0 болсын. Онда

болады. Ал біз айқын болуы ушін F'z(P₀) ≠ 0 деп алайық. Енді (§1.4. (10) және (11) қараңыз)

мәндерін S бетінің нүктедегі жанама жазықтығының

теңдеуіне қойып, оны түрлендірсек

(8)

аламыз. Бұл S: F(x,y,z) = 0 бетінің P₀=(x₀,y₀,z₀) нүктедегі жанама жазықтығының теңдеуі. Ал S-бетінің нүктедегі нормалінің (тіктеменің) теңдеуі

(9)

түріне ие болады.

Біз векторыS бетінің нормалі (тіктемі) бойынша бағытталатынын көрдік.