§ 3.4. Бip айнымалы функцияның дифференициалдық ecenтелyi

1. Туынды

нүктесінде және оның қандайда бip маңайында

анықталған функция болсын. – нүктесі деп аргумент өсімшесі ал оған сәйкес келетін функция өсімшеci

арқылы белгіленетін еді.

Анықтама. Егер шегi

бар болса, онда бұл сан y = f(x) функциясының х₀ -нүктесіндегі туындысы деп аталады да т.с.с. таңбаларының бірімен белгіленеді.Сонымен, немесе т.с.с. (1)

Егер (1) - шек немесе болса, онда функциясының - нүктедгі туындысы шексіздікке тең.

Егер (1) - теңдіктегі шектер немесе жағдайында қарастырылса, онда шек (егер ол бар болса) f функциясының х₀ нүктесіндегі оң жақ туындысы, ал немесе жағдайында қарастырылса, онда сол жақ туындысы деп аталады да олар, сәйкес, арқылы белгіленеді.

Функцияның нүктесінде туындысы бар болуы үшін:

1) 2)шарттарының орындалуы қажетті және жеткілікті. Онда (2)

Ескерту, Функция нүктеде үзіліссіз болса да, оның бip жақты туындылары болмауы мүмкін.

Ал бұған кері тұжырым үшін олай емес: х нүктесінде туындысы бар функция осы х - нүктесінде үзіліссіз болады. Бұл кері тұжырым біржақты туындылар жағдайында да орындалады.

Салдар. Егер х₀ нүктесі функциясының үзіліс нүктесі болса, онда осы нүктеде f- тің шенелген туындысы болмайды.

2. Туындының механикалық және геометриялық мағынасы

Лездік жылдамдық нүктенің түзудегі қозғалысының заңдылығын өрнектейтін функция болсын: S- нүктенің t-(уақыт) кезіндегі О нүктеден арақашытығы. t - уақыт кезіндегі лездік жылдамдық

Туындының геометриялық мағанасы.

26-сурет 27-сурет

(а,b) аралығында үзіліссіз y=f(x) функциясы берілсін. Оның Г - графигін A = (x,f(x)) нүктесін белгілеп (26 — 27 суреттер) осы нүктедегі қисыққа жүргізілген жанаманы анықтайық. Ол үшін Г -қисығынан басқа нүктесін аламыз (26 - суретте ал 27 - суретте жағдайы көрсетілген). А мен В нүктелері арқылы өтетін, х - тің өсу жағына қарай бағытталған S түзуін қиюшы деп атаймыз. Оныңх - өсінің бағытымен арасындағы бұрышын деп белгілейік және

Егер болса, онда және В нүктесі Г қисығы бойымен А - нүктесіне ұмтылады. Осыдан бұрышы қандайда бip мәніне

ұмтылса, онда шегi бар және ол f функциясының х нүктесіндегі (ақырлы) туындысына тең. Kepiciнше, erep (ақырлы) туындысы бар болса, онда

Анықтама. Г - қисығының A = (x,f(x)) нүктесіндегі жанамасы деп және нүктелері арқылы өтетін (х -тің өсу жағына қарай бағытталған) s - қиюшының - ғы ұмтылатын Т - түзуін айтады.

Аналитикалық геометриядан (х₀,у₀) нүктесі арқылы өтетін бұрыштық коэффициенті | тең түзу теңдеуі түрінде жазылатыны белгілі. Олай болса, y = f(x) қисығының нүктесіндегі жанама тендеуі

түрінде, ал нүктедегі нормаль теңдеуі түрінде жазылады.

Қорытынды. № 33-34 лекциялардан кейін студенттер туынды ұгымыын біліп, оның механикалық, геометриялық мағынасын түсінеді. Әрі элементар функциялардың туындысын табу жолын меңгереді.

№ 35-36 лекциялар. Туынды табу ережелері. Бір айнымалылы функцияның дифференциалы, қасиеттері, қолданылуы.

3. Дифференциалдау ережелері

х нүктесінде шектеулі туындысы бар функция дифференциалданатын функция деп аталады.

1-теорема. Erep u(x),v(x) х-нүктесінде дифференциалданатын функциялар болса, онда осы нүктеде олардың қосындысы, көбейтіндісі және бөліндісі дифференциалданады және

1)

3)

2 - теорема, (күрделі функцияны дифференциалдау ережесі)

функциясы нүктесінде дифференциалданатын және ал функциясынүктесіндедифференциалданатын болсын. Онда у - f[u(x)] күрделі функция нүктесінде дифференциадданады және оның туындысы

(4)

4.Kepiфункция туындысы

функциясының анықталу аймағыDмәндер аймағыЕ болсын.

Анықтама. Егер әрбір үшін g[f(x)] = х және әрбір үшін шарттары орындалса, онда анықталу аймағы Е және мәндер аймағы D болатын х = g(y) функциясы у = f(x) функциясына кepi функция деп аталады.

OXY координаталар жүйесінде y = f(x) пен x = g(y) функцияларының графиктері бipey ғана. Ал

у = f(x) пен у = g(x) функцияларыныц графиктері у-х өстерімен қарағанда симметриялы болады.

Теорема. Erep y = f(x) қанадайда бip I аралығында үзіліссіз болса, онда, оның кері функциясы болуы үшінfфункциясыIаралығында монотонды өспелі немесе кемімелі болуы қажетті және жеткілікті.

Теорема. y = f(x) [a,b] аралығында үзіліссіз, өспелі және қандайда бip нүктеде нөлге тең емес ақырлыf'(x) туындысы бар функция болсын. Ондаf- ке кері функциясында осы х нүктеде туындысы бар және ол үшін

немесетеңдігі орындалады. Енді туынды формулаларын жинақтайық. Heгізгi элементар функциялардың туындыларының кестесі.

5. Параметрмен берілген функция және оның туындысы

у-тің х-ке тәуелділігі t параметрі арқылы өрнектелсін:

у - тіңх - бойынша туындысынх пену - тіңt - бойыншатуьшдылары арқылы табайық.

Теорема. Егер және бар жәнеболса, ондаx - нүктесінде дифференциалданады және (5)

6. Функция дифференциалы

Анықтама. Егер f функциясының х - нүктесіндегі -өсімшесін

(6)

түрінде жазылатын болса,онда берілген f(x) функциясы х - нүктесінде дифференциалданады деп атайды (А- х - ке тәуелді).

Теорема. f х - нүктесінде дифференсалданатын функция болу үшін х- нүктесінде функцияның ақырлы туындысының болуы қажетті және жеткілікті.

(6) — теңдіктегі бірінші қосылғыш - ке пропорционал және оған сызықты тәуелді, ал екінші қосылғыш - ке салыстырғанда жоғары peттi шексіз аз яғни болса) - да екінші қосылғыш бірінші қосылғышқа қарағанда жылдамырақ нөлге ұмтылады. Осыған байланысты шамасын ұмтылғанда) функция өсімшесінің бас мүшесі дейді және ол функцияның дифференсалы деп аталады да dy арқылы белгіленеді.

Сонымен, dy = df(x) = (7)

Егер x-нүктесінде дифферсалданатын функциялар болатын болса, онда тұрақты сан ;

Егер x- нүктесінде, ал у = f(u) функциясы u нүктесінде дифференциалданса, онда y = f[u(x)] күрделі функциясы яғни y-f(u) үшін df = f'(u)du теңдігі u тәуелсіз айнымалы болса да, немесе функциясы болса да орындалады екен. Бұл ереже дифференциал түрінің инварианттылығы деп аталады.

теңдігінен немесе

жуық теңдігін жазуға болады, және оны жуықтап есептеулерre қолданылады .

Қорытынды. № 35-36 лекциялардан кейін студенттер туындыны есептеу ережесін меңгереді, дифференциал ұгымыын біліп, оның көмегімен жуықтап есептеу тәсілін меңгереді.

№ 37-38 лекциялар. Жоғарғы ретті туындылар мен дифференциалдар және олардың қасиеттері.Дифференциалданатын функциялар жайлы теорема.

7. Жоғарғы peттi туындылар мен дифференциалдар

Жоғарғы реттік туындыларf функцияның (а, b) аралығында туындысы бар болса, f'(x) белгілі бip функция болады. Онда бірінші туынды дейді. Өз кезіндегі бірінші туындының да (а, b) аралығында туындысы болуы мүмкін. Бұл жағдайда оны f функциясың екінші туындысы немесе екінші peттi туындысы дейді де немесе арқылы белгілейді .

Жалпы, f- тің ретті туындысының брінші peттi туындысы f функцияның n – ші ретті туындысы деп атайды да

немеседеп белгілейді.

Мысалдар:1.

2.шынында да,

3.

п - рет дифференциалданатын u(х) және v(x) функцияларыныц қосындысы мен көбейтіндісі үшін келесі дифференциалдау ережесі орындалады:

1.

2. Лейбеиц формуласы:

Мұнда Бұл теңдіктерді математикалық индукция әдісін пайдаланып дәлелдеуге болады.

Жоғарғы рет дифференциал. (а,b) аралығында n -рет дифференциалданатын функция, х –тәуелсіз айнымалы(яғни dx x -ке тәуелсіз кез келген сан) болсын. Онда f функциясының х нүктесідегі dy = f\x)dx бірінші дифференциалынан алынған дифференциал f функциясының екінші дифференциалы деп аталады да арқылы белгіленеді. Ол

тең. y=f{x) функциясының n - peттi дифференциалы деп f функциясыньң (n-1) - ретті дифференциалының дифференциалын айтады және оны келесі түрде белгілейді.

. n —ші ретті дифференциал үшін

(8)

теңдігі орындалады. n —ші ретті дифференциалдар үшін келесі ережелер орындалады:

1.

2)

8. Дифференциалданатын функциялар туралы теоремалар

Анықтама. Егер

теңсіздігі орындалатындай с - нүктесінің маңайы табылса, онда f функциясы х=с нүктесінде локальді максимумге (сәйкес, минимумге) ие болады дейді.

Локальді (төңіректік) максимум немесе минимум локальді экстремум деп аталады. 28 -суретте[а,b] -де үзіліссіз функция бейнеленген. меннүктелері - f -тің локальді минимум нуктелері, алмен -локальді максимум нуктелері;аменb локальді экстремум нүктелері бола алмайды (өйткені, fбұл нүктелердің толық маңайында анықталмаған), алайда,b -локалды

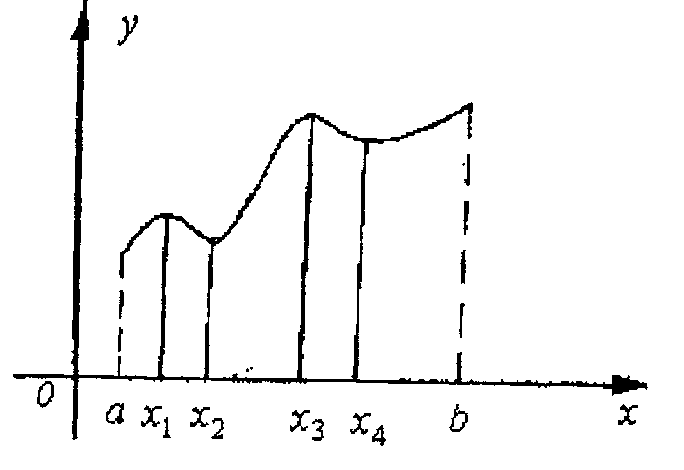
28-сурет

біржақты максимум, а -локальді біржақты минимум нүктелері деп айтуға болады.

1 -теорема (Ферма). Егер fфункциясыныңс —нүктесінде туындысы бар және ол осы нүктеде локальді экстремумға ие болса, онда

2 -теорема (Ролль). Егеру= f(x) [a,b] —де узіліссіз,(а, b}-да Дифференциалданатын функция жәнеболса, ондатеңдігі орындалатындай нүктесі табылады.

3 -теорема (Коши). Егерf(x)пенg(x)функциялары[a,b] — де үзіліссіз(a,b) -да дифференциалданатын және болса, онда

теңдігі орындалатындай нүктесі табылады.

4 - теорема (Лагранж). f(x) [а, b] — де үзіліссіз және (а, b) — да - дифференциалданатын функция болсын. Онда

(10) теңдігі орындалатын нүктесі табылады.

5 - теорема, [а, b] — кесіндісінде үзіліссіз және (а, b) — да туындысы теріс емес (оң) болатын функция [а, b] — де кемімейді (өседі).

6 - теорема. Егер функцияның (а, b) —ғы туындысы нольге тең болса, онда ол(а, b) — да тұрақты, яғни

Анықтама. Егер нүктесінің қандайда бip | маңайының әpбip х#х₀ нүктесі үшін

.

теңсіздігі орындалса, онда х₀ — нүктесінде y = f(x) функциясы өceді (кемиді) дейді.

7 - теорема. Егер онда y = f(x) функциясы - нүктесінде өседі (кемиді).

Қорытынды. № 37-38 лекциялардан кейін студенттер жоғарғы ретті туындылар мен дифференциалдарды табу ережелерін меңгеріп олады есептей алады.

№ 39-40 лекциялар. Туындылар мен дифференциалдардың қолданылуы. Лопиталь ережесі мен Тейлор қатары.

9. Лопиталь ережесі

Лопиталь ережесі және т.б. анықталмаған өрнектердің шегін функциялардың туындыларының қатынасының шегі арқылы есептеуге әкеледі.

Теорема (Лопиталь ережесі). f(x) пен g(x) х = а нүктесінің маңайында (а-нүктесі алыньш тасталуы да мүмкін) анықталған, | дифференциалданатын және ( немесе), a- нүктесінің маңайында шарттары орындалатын. функциялар болсын. Онда, егер - шегі бар болса, онда шегі де бар және = теңдігі орындалады.

Егер өрнегі де-түріндегі анықталмағандық болып функциялары теорема шартын қанағаттандырса, онда ==

Бұл теңдіктерді, егер үшінші шек (бар) болса, онда екінші және бірінші шектерде (бар) болады деп түсінуі керек. түріндегі анықталмағандықтар алгебралық түрлендірулер арқылы - немесе — анықталмағандығына келтіріледі.

а) анықталмағандығын

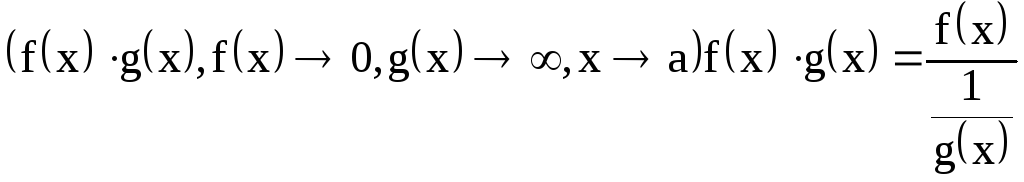түрлендіруі ал 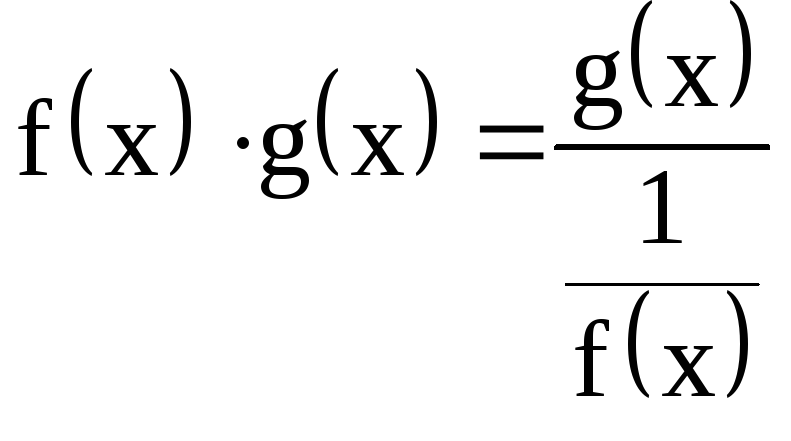- түрлендіруі — түріне әкеледі.

б) анықталмағандықтарын түрледірулер арқылы түріне (а - жағдайына) келпруге болады.

в) анықталмағандығын - түріне келтіруге болады:

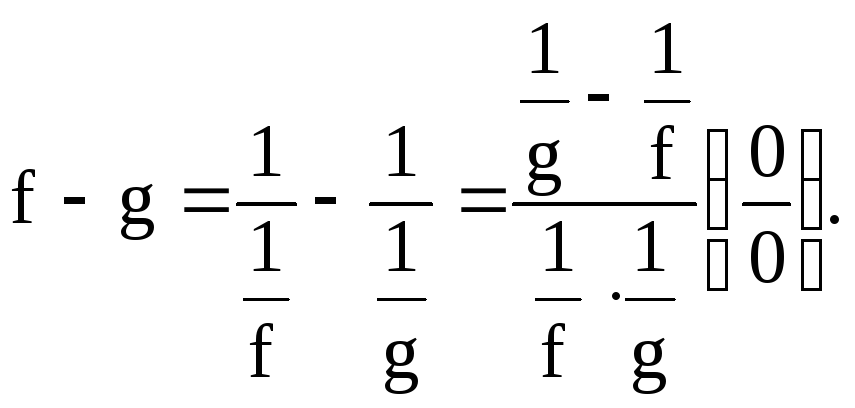
10. Тейлор формуласы

Көпмүшелікке арналған Тейлор формуласы. Берілген

(13)

көпмүшелігін х-х₀ биномы (х₀ - қандайда бip сан) бойынша жіктеу керек болсын. Бұл есепті шешудің әдістерінің бipi төмендегідей.

(14)арқылы ізделінген жіктелуді белгілеп А₀,А,,...,Аn- коффициенттерін табайық. (14) — те х = х₀ деп алсақ А₀=Р(х₀) аламыз. дифференциалдасақ

шығады да, бұдан х=х₀ деп алсақ табамыз. Екінші peт дифференциалдаудан соң

-шығады да, бұдандеп алсақ Осы процесті қайталай берсек келесі жалпы формула шығатынын көру қиын емес (оны математикалық индукция әдісімен дәлелдеуге болады).

Бұл коэффициенттерді (13)-ке қойып көпмүшелкке арналған Тейлор формуласын аламыз: \

нсмесе қысқаша

Функцияларға арналған Тейлор формуласы.

1 - теорема. Егер f функциясы х₀ нүктесінің қандайда бip маңайында n — рет үзіліссіз дифференциалданса, онда үшін келесі теңдік орындалады:

(14)

(14) - теңдікті Пеано мағынасындағы қалдық мүшесі бар Тейлор формуласы деп атайды.

Дербес жағдайда х₀ =0 болса, онда (14) - тендік келесі түрге ие болады:

(15)

(15) - теңдік Пеано түріндегі (мағынасындағы) қалдық мүшесі бар Маклорен формуласы деп аталады.

Егер маңайында функцияның үзіліссіз туындысы бар болса, онда қалдық мүшені дәлірек жазуға болады.

2 - теорема. Егер — нүктесінің маңайында f функциясының (n + l)-i үзіліссіз туындысы бар болса, онда кез келген үшін

(16)

теңдігі орындалатындай нүктесі табылады.

(16) - теңдік Лагранж түріндегі қалдық мүшесі бар Тейлор формуласы деп аталады. (16) - теңдікте болса, онда Лагранж түріндегі қалдығы бар Маклорен формуласын жазуға болады:

(17)

(мұндағы х оң немесе тepic болуы мүмкін).

Ескерту. Тейлор формуласының қалдық мүшесінің басқа да түрлері бар екені белгілі. Мысалы, Коши түріндегі қалдық мүше

түрінде жазылады.

Қорытынды. № 39-40 лекциялардан кейін студенттер туындыны пайдаланып Лопиталь ережесімен анықталмағандықтарды шеше алады және Тейлор қатарына функцияны жіктей отырып оның жуық мәнін таба алады.

№ 41-42 лекциялар. Туынды көмегімен функцияның өсу, кему аралықтарын табу. Функция экстремумдарын табу. Функцияны экстремумға зеттеу.