§4.7. Көп айнымалы функциялардың экстремумдері

Экстремумнің қажетті, жеткілікті шарттары

Анықтама. Егер (х₀, у₀) нүктесі үшін

теңсіздігі орындалатындай U(x₀,y₀) маңайы табылса, онда z = f(x,y) функциясы (х₀,у₀) нүктесінде локальдік (төңіректік) максимумге (минимумге) ие болады дейді.

(х₀,у₀) - нүктесін локальдік максимум (минимум) нүктесі, ал функцияның ол нүктеге сәйкес мәнін – функцияның максимум (минимум) мәні деп атайды. Локальдік максимум мен минимум мәндері жалпы атаумен - локальдік экстремум деп аталады. Экстремум анықтамасынан (х₀,у₀) нүктесінің жеткілікті шағын (аз) маңайында функция өсімшесі: ∆f= f(x,y)-f(х₀,у₀) таңбасын өзгертпейтінін көреміз:

локальдік максимум (max) үшін ∆f 0;

локальдік минимум (min) үшін ∆ f ≥ 0.

Енді, алдымен, экстремумнің қажетті шартын дифференциалданатын функциялар үшін қарастырамыз.

Теорема (экстремумнің кажетті шарты). Егер дифференциалданатын z = f(x,y) функциясының P₀(х₀,у₀) нүктесінде экстремумі бар болса, онда оның осы нүктедегі дербес туындылары нөлге тең:

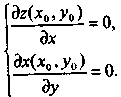
Салдар. Егер P₀(х₀,у₀) нүктесінде дифференциалданатын z = f(x,y) функциясы осы P₀ нүктеде экстремумге ие болса, онда

1-Ескерту. f функциясының P₀(х₀,у₀) нүктесінде экстремумі болуы үшін (1) - шарт жеткілікті бола алмайды.

Егер f функциясының үзіліссіз дербес туындылары үшін P₀(х₀,у₀) нүктесінде 1- шарт орындалса, онда Р₀ - f(x,y) функциясының стационар нүктесі деп аталады.

z = f(x,y) бетінің Р₀(х₀,у₀) - стационар нүктесіндегі жанама жазықтығының, теңдеуі

Z = Z₀

түрінде жазылады. Өйткені, бұл нүктеде (1) шарт орындалады да, жанама жазықтық теңдеуінің, яғни

теңдеуінің оң жағы нөлге тең болады.

Дифференциалданатын z = f(x,y) функциясының Р₀(х₀,у₀) нүктедегі экстремумнің жеткілікті шартының геометриялық, мағынасы - функция графигінің осы нүктедегі жанама жазықтығының x,y – тәуелсіз айнымалылар жазықтығына параллель болатынын көрсетеді.

2-ескерту. Берілген нүктелерде үзіліссіз функцияның дифференциалы жоқ болса да ол нүктелер экстремум нүктелері болуы мүмкін.

f функциясының стационар нүктелері мен оның дифференциалданбайтын нүктелерін - критикалық (күндікті) нүктелер деп жалпы түрде атайды.

Экстремумнің жеткілікті шартын жалпы жағдайда келесі түрде тұжырымдауға болады.

Р₀(х₀,у₀) нүктесі z = f(x,y) функциясының стационар нүктесі, ал функция Р₀ нүктесінің қандайда бір маңайында екі рет дифференциалданып Р₀ нүктесіндегі барлық екінші ретті дербес туындылары үзіліссіз болсын. Онда:

1) егер екінші ретті дифференциал x, y өсімшелерінің функциясы ретінде, бір мезгілде нөлге тең емес х,у-тің барлық мәндер жиынтығында тұрақты таңба сақтаса, ондаz = f(x,y) Р₀-нүктесінде экстремумге ие болады, атап айтқанда, d²z(Р₀, x,y)<0 болса - максимум,

d²z(Р₀, x,y)>0 болса — минимум

қабылдайды;

2) егер d²z(Р₀, x,y)x,y -тің таңба айнымалы функциясы болса, ондаР₀ -нүктесінде функция экстремум қабылдамайды;

3) егер d²z(Р₀, x,y)0 немесе d²z(Р₀, x,y)0 болып, екінші дифференциал нөлге тең болатынх,у мәндер жиынтығы (х,у-бір мезгілде нөлге тең емес) бар болса, онда қосымша зерттеу қажет болады.

2. Функцияның ең үлкен және ең кіші мәндері. Егер f(P) функциясы шектелген тұйық аймақта: үзіліссіз дифференциалданса, онда f функциясы өзінің ең үлкен және ең кіші мәндерін стационар нүктелерде немесе аймақтың Г шекарасындағы нүктелерде қабылдайды.

3. Шартты экстремум. Практикада тәуелсіз айнымалылардың емес, қандай да бір қосымша шарттар арқылы байланысқан (мысалы, қандай да бір берілген теңдеулерді қанағаттандыратын) көп айнымалылар функциясының максимумы мен минимумын табуға арналған есептер жиі кездеседі.

х пен у айнымалылары

тендеуімен байланысқан (оны байланыс теңдеуі деп атайды)

функцияның максимумі мен минимумін табу керек болсын.

Егер (2)-теңдеуді у-ке қатысты шеше алсақ, (мысалы, y = (x)),онда оны (3)-гі y-орнына қойып

бip айнымалы функциясын алар едік. Бұл функцияның экстремум қабылдайтын х-нүктесін тауып, байланыс теңдеуінен осы х-нүктеге сәйкес келетін y-мәнін анықтап есептің шешімін аламыз. Алайда қойылған eceпті, (2)-байланыс теңдеуін y-ке (немесе х-ке) қатысты іздемей-ақ шешуге болады.

(З)-тен табамыз (y-ті х-тің функциясы деп аламыз):

Экстремум нүктелері үшін

теңдігі орындалу тиіс. (3)- байланыс теңдеуінен

аламыз. (5)-теңдікті қазірше белгісіз коэффициентіне көбейтіп, нәтижесін (4)-ке мүшелеп қосамыз:

немесе

(6)-теңдік барлық, экстремум нүктелерінде орындалады. Енді -санын (анықтық. үшін критикалық нүктелердеболсын)

теңдігі орындалатындай етіп таңдап алсақ онда (6)-тен

шығады. Сонымен, экстремум нүктелерінде х,у,- белгісіздері бар келесі үш теңдеу қанағаттандырылады:

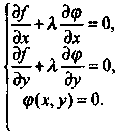
(7)-ден х,у жене табамыз. Мұнда-белгісізі тек көмекші роль атқарады, бұдан кейін оның бізге қажеті болмайды.

(7)-дің сол жағы-

функциясының х,у, айнымалылары бойынша дербес туындылары екенін байқаймыз

(8)-түрдегі функция Лагранж функциясы, -Лагранж көбейткіші, ал шартты экстремум есебіне қолданылған әдіс -Лагранж көбейткіштерінің әдісі деп аталады.

(7)-теңдеулер-шартты экстремумнің қажетті шарты ғана болатынына назар аудару керек, яғни (7)-ді қанағаттандыратын х,у (жене ) мәндерінде шартты экстре­мум болмауы да мүмкін. Табылған(х, у) -стационар нүктесінде шартты экстремум бар немесе жоқ, екенін білу үшін Лагранж функциясының екінші дифференциалының таңбасын зерттеу қолайлы. Бірақ dy дифференциалы dx-ке тәуелді болатыны есте тұруы керек.

Қорытынды. № 47-48 лекциялардан кейін студенттер көп айнымалылы функцияның шартты және шартсыз экстремумдарын табуды үйреніп оның практикалық маңызын білетін болады

№ 49-50 лекциялар. Комплекс сандар оның қасиеттері және оған қолданылатын амалдар. Рационал бөлшектер.

5 ТАРАУ

ИНТЕГРАЛДАР