2. Анықталған интегралдардың касиеттері
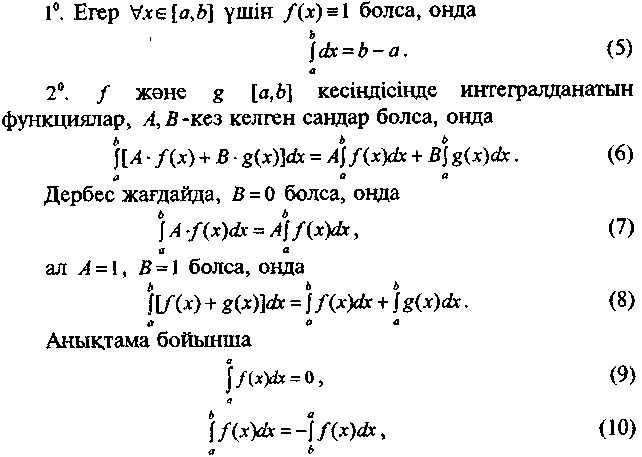
деп аламыз.
3°. Анықталған интегралдың аддитивтік (қосымдылық) қасиеттері. Егер кез келген а,b,с сандары ушін әpбip [a,b], [а,с] жэне [с, b] кесінділерінде интегралданатын функция болса, онда келесі теңдік орындалады
(11)
4°. Eгep f пен g [a,b] кесіндісінде интегралданатын функциялар болса және
x
[a,b],
f(x)≤g(x)
тецшздт орындалса, онда
(12)
5°. Егер f пен | f | [а, b] кесіндісінде интегралданатын функциялар болса, онда
(13)
§5.9. Интегралдан оның жоғары шегі арқылы туынды алу
f функциясының интегралдық қосындысы
түрінде жазылатындықтан, интегралдау айнымалысын кез келген әріппен көрсетуге болады:
Біз төменде интегралдау айнымалысын, оқырманға түсінікті болу үшін, ыңғайлы әріппен алмастырып отыратын боламыз.
f
[а,b]
кесіндісінде
интегралданатын функция болсын. Онда
ол кез келген х
[а,b]нүктсі
үшін [а,х]
кесіндісінде
де интегралданады (дәлелдеусіз
қабылдаймыз). Мысалы, [а,b]
кесіндісінде
үзіліссіз немесе монотонды функция
[а,х]
[а,b]кесіндісінде
де, сәйкес, үзіліссіз немесе монотонды,
демек, интегралданады.
Әpбip
x
[a,b]санына
анықталған
-
мәні
сәйкес
келеді, яғни
(1)
- интегралдың жоғары шегіне тәуелді функция.
1-теорема. Егер f [а,b] кесіндісіне интегралданатын функция болса, онда
функциясы
кез келген x
[a,b]нүктесінде
үзіліссіз болады.
2-теорема.
Егер
f
[а,b]
кесіндісіне
интегралданатын және x
[a,b]нүктсінде
үзіліссіз функция болса, онда осы х
нүктесінде
F'(x)
- туындысы
бар және
(2)
теңдігі орындалады.
Басқаша
айтқанда, [а,b]
кесіндісінде үзіліссіз f(x)
функциясының
осы кесіндіде алғашқы функциясы бар
болатыны
шығады және ол алғашқы функцияның бipi
ретінде
алуға болады:
(3)
§ 5.10. Ньютон-Лейбниц формуласы және оның анықталған
интегралдарды есептеуге қолданылуы
f [а,b] – кесіндісінде үзіліссіз функция, ал Ф(u) оның осы кесіндідегі қандай да бip алгашқы функциясы болса, онда
(1)
теңдігі орындалады. (1) — Ньютон-Лейбниц формуласы деп аталады.
1-теорема (айнымалыны алмастыру туралы). Егер φ(t) функциясы [c,d] кесіндісінде үзіліссіз дифференциалданатын және а=φ(с), b=φ(d) болып, сонымен бipгe f(x) [а,b] кесіндісінде үзіліссіз функция болса, онда келесі теңдік орындалады '
(2)
Келесі теңдіктерді анықталған интегралды есептеуде жиі пайдаланады:
1) Егер f жұп функция болса (f (-u)= f (u)), онда
(3)
2) Егер f тақ функция болса (f (-u)= -f (u)), онда
(4)
2-теорема. Егер и(х) пен v(x) [a,b] кесіндісінде үзіліссіз дифференциалданатын функциялар болса, онда келесі бөлікпен интегралдау формуласы орындалады:
(5)
3-теорема. (орта мән туралы), [a,b] кесіндісінде үзіліссіз f(x) функциясы үшін
(6)
§ 5.11. Меншіксіз интегралдар
1. Бірінші және екінші текті меншіксіз интегралдар. Біз осыған дейін анықталған интегралдар туралы айтқанда интегралдау аралығы шектелген және интеграл астындағы функция осы аралықта шенелген деп қабылдадық. Бірақ анықталған интеграл анықтамасын шексіз интегралдау аралығы үшін және шенелмеген функция жағдайына арнап зерттеу қажеттігі жиi кездеседі. Енді осы сұрақтарды қарастырайық.
I. а) f функциясы [а,+∞) аралығында берілсін;
б)
f
- кез келген ақырлы [а,b']
кесіндісінде
(мұндағы b'
(a,+∞)интегралданатын
болсын.
Егер
(1)
шегі болса, онда ол шек f функциясының [а,+∞) аралығындағы (бipінші текті) меншіксіз интегралы деп аталады да келесі түрде белгіленеді
II. а) f-шекті [а,b) аралығында берілген және b-нүктесінің маңайында шенелмеген функция;
б) f - кез келген [а,b'] кесіндісінде (а< b'< b) интегралданатын функция болсын.
Егер
(2)
шегі болса, онда ол шек f функциясының [а,b] кесіндісіндегі (екінші текті) меншіксіз интегралы деп атайды да оны
деп жазылады.
Егер f функциясы үшін I немесе II шарттың тек бipi ғана орындалса, онда
(3)
өрнегін жалғыз ерекшелігі b-нүктесінде болатын интеграл деп атайтын боламыз.
Осы сиякты жалғыз ерекшелігі а-нүктесінде болатын интегралды да анықтауға болады. Бұл жағдайда I және II шарттар келесі түрде тұжырымдалады:
I. а) f функциясы (-∞;а] аралығында берілген
б) f - кез келген ақырлы [а',b] кесіндісінде (-∞<а'<а) интегралданатын функция.
II. а) f – шекті (a,b] аралығында берілген және а-нүктесінің маңайында шенелмеген функция;
б) f - кез келген [а', b] кесіндісінде (а<а'< b) интегралданатын функция.
Егер меншіксіз интеграл астындағы функцияның алғашқы функциясы бeлгiciз болса, онда оның жинақтылығы туралы айту қиын. Ондай жағдайларда, кейде алғашқы функцияны керек етпейтін арнайы белгілерді пайдаланып, интеградың жинақты немесе жинақсыз болатындығын білуге болады. Енді осы сұрақтарға көшейік.
2. Меншіксіз интегралдардың жинактылық белгілері. Таңбасы тұрақ емес функция интегралын зерттеуге арналған келесі түciнікті енгізейік. Егер
(4)
интегралы жинақты болса, онда
(5)
интегралы абсолют жинақты болады дейді; Егер (5) - жинақты, ал (4) - жинақсыз интеграл болса, онда (5) - интеграл шартты жинақты деп айтады.
Ескертпе.
Егер
f(x)≥о,
х[а,)
болса онда (5) интегралдың
жинақтылығы мен жинақсыздылығынан
сәйкес
Tepic емес функциялардың меншіксіз интегралдарын жинақтылыққа зерттейміз.
1-теорема. Жалғыз ерекшілігі b- нүктесінде болатын
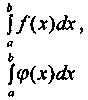
интегралдары үшін [а,b) аралығында
(8)
теңсіздіктері орындалсын. Онда
теңсіздігі орындалады және (7)-интегралдың жинақтылығынан (6)-интегралдың да жинактылығы, ал (6)-интегралдың жинақсыздылығынан (7)-интегралдың да жинақсыздығы шығады.
2-теорема. (6) және (7) интегралдардың ерекшелігі жалғыз b нүктесінде болсын. Егер интеграл астындағы функциялар оң және
(9)
болса, онда (6), (7) интегралдар бір мезгілде жинақты немесе бip мезгілде жинақсыз.
Қорытынды. № 57-58 лекциялардан кейін студент анықталған интегралды есептеу тәсілдерін меңгеріп оның қолданыстағы мағынасын білетін болады.
№ 59-60 лекциялар. Анықталған интегралдың көмегімен шығарылатын есептер қарастырылады. Оларды шешу жолдары көрсетіледі.