§4.3. Туындылар мен дифференциалдар

1. Дербес туындылар. f(х,у) функциясының Р(х,у) нүктесіндегі х бойынша дербес туындысы деп ∆_xz дербес өсімшесінің ∆х өсімшесіне қатынасының ∆х→0 (ұмтылғандағы) шегін (егер ол шек бар болса) айтады да

символдарыньң біреуімен белгілейді:

f(x,y) функциясының Р(х,у) нуктесіндегі у бойынша дербес туындысы да дәл осылай анықталады және ол

символдарыньң біреуімен белгілейді:

Бұл анықтамадан дербес туындьларды есептеу ережелері бip айнымалы функцияның туындьларын есептеу ережелерімен бірдей екенін көреміз. Әрине, бұл жағдайда дербес туынды айнымалылардың қайсысы бойынша ізделініп отырғаны есте тұру керек, ал қалған айнымалылар тұрақты сан ролін атқарады.

2. Толық дифференциал. ашык, жиындаz = f(x,y) функциясы берілсін және оның нүктесінде үзіліссіз дербес туындылары бар болсын. Бұдан(х,у) нүктесінің қандай да бip маңайында осы дербес туындылар бар болатыны (олар (x,у)-тен баска нүктелерде үзілісті болса да) шығады. (∆х, ∆у) өсімшесін

шартын қанағаттандыратындай, ал δ>0 санын (x+Δх, у+Δу) нуктесі жоғарыдағы көрсетілген маңайдан шығып кетпейтіндей жеткілікті аз етіп алып, осы (Δх,Δу) есімшеге сәйкес келетін f функциясының өсімшесін қарастырайық:

Мұнда бірінші квадрат жақшада тұрған өрнекті айнымалысы жалғыз х болатын функцияның (екінші аргумент тұрақты у+Δу мәнін сақтайды) екі мәнінің айырмасы, ал екінші квадрат жақшада тұрған өрнекті айнымалысы жалғыз у болатын функцияның (х-мәні тұрақты) екі мәнінің айырмасы eтіп қарастыруға болады. Бул айырмаларға Лагранждың орта мән туралы теоремасын қолданып

(1)

аламыз (мұндағы ). Дербес туындылар(х,у) нүктесінде үзіліссіз болғандықтан және ескерсек

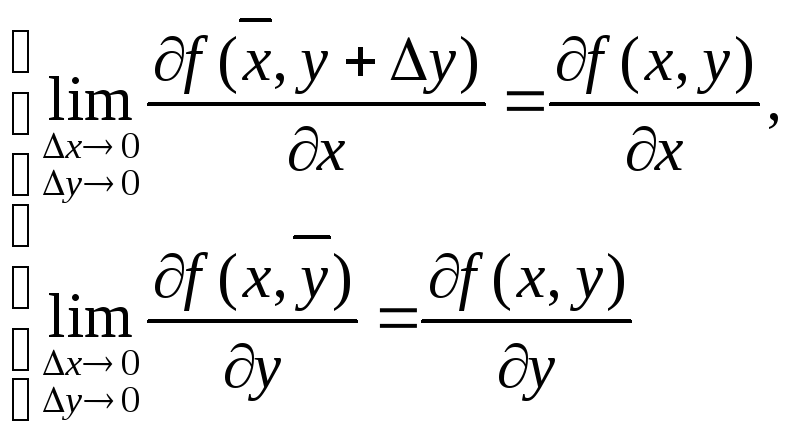
Бұл теңдіктерді

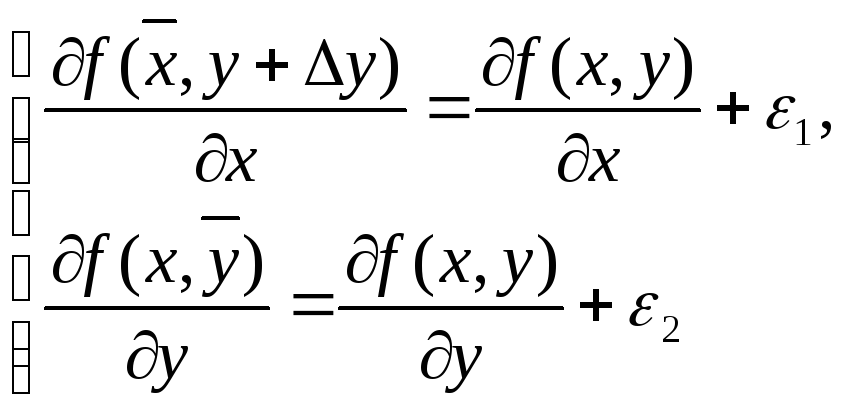(2)

түрінде жазуға болады. Мұнда ε₁ мен ε₂

(3)

ұмтылатын шамалар. (2)-ті (1)-ке қойсақ

(1′)

аламыз. Бұл теңдіктегі соңғы екі қосылғыштардың қосындысы шамасымен салыстырғанда жоғары peттi шексіз аз шама:

Шынында да, ∆х, ∆у ≤ ∆ρ болатындықтан ∆ρ→0 ұмтылса, онда ((3)-ті қараңыз)

Біз кeлeci маңызды теореманы дәлелдедік.

1-теорема. Егер z = f(x,y) функциясыныц (х,у) нүктесінде үзіліссіз дербес туындылары бар болса, онда оның осы нүктедегі жеткілікті аз (∆х,∆у)-ке сәйкес өсімшесін келесі формула түрінде жазуға болады

(4)

(4)-теңдіктегі дербес туындылар ∆х,∆у-ке тәуелді емес. Сондықтан теорема шартынан функция өciмшесін кeлeci формула түрінде жазуға болатыны шығады:

(5)

(мұндағы А мен В сандары ∆х,∆у -ге тәуелді емес).

Анықтама. Егер f функциясының (х,у) нүктедегі өсімшесін жеткілікті аз (∆х,∆у) үшін (5) теңдік түрінде жазуға болатын болса, онда f функциясы (х,у) нүктесінде дифференциалданады дейді.

(5) теңсіздіктегі А∆х + В∆у қосылғышы (∆х,∆у) бойынша сызықты функция. Ол ∆f өсімшесінің сызықты бас бөлігі деп аталады, ал қалған қосылғышы (∆х,∆у) өсімшелерімен күрделі тәуелділікте болады, бірақ ол қосылғыш ∆х пен ∆у-ке салыстырғанда нөлге жылдамырақ ұмтылады.

Егер f функциясы (х,у) нүктесінде дифференциалданса, яғни (5) теңдік орындалса, онда оның осы нүктеде

(6)

тендіктері орындалатындай дербес туындылары болады. Мысалы, (5) теңдіктегі ∆х = h, ∆у = 0 деп алсақ, онда (∆ρ = h→0)

∆z = ∆_xz = Ah + o(h), h→0

ол бұдан

аламыз.

Бұл айтылғандардан келесі теорема шығады.

2-теорема. f функциясы нүктеде дифференциалдануы үшін оның осы нүктеде дербес туындыларының болуы қажетті, ал оның осы нүктеде үзіліссіз дербес туындыларының болуы жеткілікті.

Бір айнымалы f функциясының х нүктесінде дифференциалдануы ушін оның осы нүктеде туындысы болуы қажетті және жеткілікті болатын еді.

Анықтама. Егер f функциясы (х,у) нуктеде дифференциалданса, онда оның өсімшесінің осы нүктедегі сызықты бас бөлігі f функциясының (толық) дифференциалы деп аталады, dz немесе df аркылы белгілінеді:

(6)

∆х, ∆у- тәуелсіз айнымалылар өсімшелерін х пен у тәуелсіз айнымалыларының дифференциалдары деп атайды да оларды dx жэне dy арқылы белгілейді. Онда толык, дифференциал келесі түрге ие болады:

(7)

3. Бетке жанама жазықтық. Толық дифференциалдың геометриялық көpiнici.

S бет S: z = f(x,y) функциясымен сипатталсын және бұл функцияның х, у жазықтығындағы қандай да бip аймақта үзіліссіз дербес туындылары болсын.

S бетінің M₀(x₀,y₀,z₀), z₀=f(x₀,y₀) нуктесіндегі жанама жазықтығы деп

(8)

теңдеуімен берілген жазықтықты айтады. Мұндағы, X,Y,Z - айнымалы (ағымдық) координаталар, ал -тің дербес туындыларының Р₀(х₀,у₀)- нүктедегі мәндері.

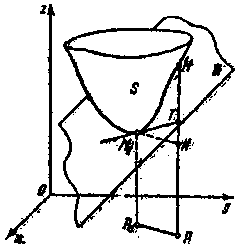
24-сурет

(8) жазыктықты П деп белгілеп, оньң қасиетін қарастырайық. х,у жазықтығында Р₀(х₀,у₀) нүктесіне жақын етіп Р(х,у) нүктесін алайык, (24-сурет). Р нүктесі арқылы өтетін z өсіне параллель түзу П жазықтығының Т нүктесіне, ал S бетінің М нүктесінде өтеді.

М - нүктесінің аппликатасы z = f(x,y), ал Т – нуктесінің аппликатасы

болғандықтан М мен Т нүктелерінің ара қашықтығы

(9)

тең. Р мен Р₀ нүктелерінің ара қашықтығы

Шарт бойынша f функциясының (х₀,у₀) нүктесінде үзіліссіз туындылары бар болғандықтын, f функциясы осы нүктеде дифференциалданады. Сондықтан, (9)-ің оң жағындағы өрнек (функция өciмшесі мен дифференциалының айырымы ретінде) ρ-ға салыстырғанда нөлге жылдамырақ ұмтылады:

|МТ| = о(ρ), ρ→0.

Сонымен, S бетінің M₀(x₀,y₀,z₀) нүктесіндегі жанама жазықтық келесі қасиетке ие болады екен: S бетінің кез келген (x,y, f(x,y)) нүктесінен z - өсінің бағыты бойынша П жазықтыққа дейінгі қашықтық Р(х,у); Р₀(х₀,у₀) нүктелерінің ара қашықтығына салыстырғанда ақырсыз аз шама.

(8) теңдіктің оң жағы f функциясының (х₀,у₀) нүктедегі (х – х₀, у – у₀) өсімшеге сәйкес дифференциалы

ал сол жағы - жанама П жазықтығының аппликатасының сәйкес өciмшесі.

Олай болса, f функциясының (х₀,у₀) нүктесіндегі (х-х₀,у-у₀)-ге сәйкес дифференциалының геометриялық мағынасы - z=f(x,y) бетіне (х₀,у₀) нүктеде жүргізілген жанама жазықтық нүктесінің аппликатасының осы (х– х₀, у - у₀) -ге сәйкес өciмшесі.

Беттің нормалі (тіктемі) деп жанама жазықтықтың бетке жанау нүктесінен өтетін осы жанама жазықтыққа перпендикуляр түзуді айтады.

Егер S беті z=f(x,y) функциясы арқылы берілсе, онда оның Р₀(х₀,у₀) нүктесіндегі тіктемінің, теңдеуі

арқылы жазылады.

Егер S беті F(x,y,z) = 0 теңдеуімен берілсе, онда оның M₀(x₀,y₀,z₀) нүктесіндегі жанама жазықтығының тендеуі

ал нормаль тендеуі

түрлерінде жазылады.

4. Толық дифферендиалдың жуықтап есептеулерге қолданылуы

Егер ∆x пен ∆y жеткілікті аз шама болса, онда функцияның толық өсімшесі мен толық дифференциалы арасында жуық теңдік жaзуға болады:

немесе

Бұдан х₀ + ∆x = х, у₀ + ∆у = у деп алып келесі жуық теңдікті жаза аламыз:

(10)

Біз (10) формуладан f(x, у) функциясын (х₀,у₀) нүктесінің маңайында сызықтық функциямен алмастыруға болатынын көреміз.

Геометриялык, тұрғыдан ол z=f(x,y) бетінің шағын бөлігі осы бөліктің M₀(x₀,y₀,z₀) нүктесінде жүргізілген жанама жазықтықтың сәйкес бөлігімен ауысқанын көрсетеді.

(10) формула f(x,y) функциясының мәндерін (егер х х₀-ге, ал у у₀-ге жақын алынса) белгілі f(x₀,y₀), f ′_x(x₀,y₀), f ′_y(x₀,y₀) мәндері бойынша жуықтап есептеуге мүмкіндік береді