
- •Академия управления при Президенте Республики Беларусь
- •Содержание
- •Тема 4. Функции 9
- •Тема 5. Дифференциальное исчисление функций одной переменной 34
- •Тема 6. Исследование функций 45
- •Тема 7. Пространство 66
- •Тема 8. Неопределенные интегралы 100
- •Тема 9. Определенные интегралы 114
- •Тема 10. Понятие кратного интеграла 132
- •Тема 11. Ряды 140
- •Тема 12. Дифференциальные уравнения 171
- •Тема 4. Функции Лекция 15. Функции
- •Основные понятия
- •Понятие числовой последовательности
- •Сходящиеся последовательности
- •Бесконечный предел
- •Замечательные пределы
- •Принцип сходимости
- •Предел функции. Теорема Гейне
- •Односторонние пределы
- •Пределы на бесконечности
- •Бесконечные пределы
- •Непрерывность функции
- •Непрерывность композиции
- •Точки разрыва
- •Контрольные вопросы к теме №4
- •Тема 5. Дифференциальное исчисление функций одной переменной Лекция 16. Дифференциальное исчисление функций одной переменной
- •Определение и смысл производной
- •Построение касательной к графику функции
- •Экономический смысл производной
- •Эластичность функции
- •Дифференцируемость функции
- •Правила дифференцирования
- •Производная сложной функции
- •Производная обратной функции
- •Дифференциал
- •Приближенные вычисления
- •Свойства дифференцируемых функций
- •Правила Лопиталя
- •Монотонность функции
- •Локальный экстремум
- •Исследование стационарных точек
- •Глобальный экстремум
- •Выпуклость и перегибы графика функции
- •Исследование функции и построение графика
- •Интерполяция и аппроксимация функций
- •Интерполяционный полином Лагранжа
- •Формула Тейлора
- •Основные разложения
- •Понятие об эмпирических формулах
- •Контрольные вопросы к теме №6
- •Тема 7. Пространство Лекция 18. Пространство
- •Точки, расстояние. Множества в
- •Последовательности в. Сходимость
- •Функции в. Предел. Теорема Гейне
- •Непрерывность функции в
- •Непрерывность на множестве
- •Теоремы о непрерывности
- •Дифференцируемость функций в. Частные производные
- •Дифференциал функции нескольких переменных
- •Необходимые условия дифференцируемости. Достаточные условия
- •Дифференцирование функции, заданной неявно и композиции функций
- •Полные дифференциалы и частные производные высших порядков. Признак полного дифференциала
- •Формула Тейлора
- •Локальный экстремум функции нескольких переменных. Необходимое и достаточное условия. Исследование стационарных точек
- •Условный экстремум функций нескольких переменных. Глобальный экстремум
- •Метод наименьших квадратов
- •Контрольные вопросы к теме №7
- •Свойства неопределенного интеграла
- •Замена переменных
- •Интегрирование по частям
- •Интегрирование рациональных функций. Метод рационализации
- •Вычисление
- •Вычисление
- •Вычисление
- •Вычисление
- •Контрольные вопросы к теме №8
- •Тема 9. Определенные интегралы Лекция 20. Определенные интегралы
- •Интегральные суммы
- •Необходимое и достаточное условие интегрируемости
- •Равномерно непрерывные функции
- •Интегрируемость непрерывных, разрывных и монотонных функций
- •Основные свойства определенного интеграла
- •Оценки интегралов. Формулы среднего значения
- •Основные правила интегрирования
- •Приложения определенного интеграла Площадь плоской фигуры
- •. Объемы тел вращения
- •Несобственные интегралы
- •Интегрирование неограниченных функций
- •Интегрирование по бесконечному промежутку
- •Приближенное вычисление определенных интегралов
- •Формула прямоугольников
- •Формула трапеций
- •Контрольные вопросы к теме №9
- •Тема 10. Понятие кратного интеграла Лекция 21. Понятие кратного интеграла
- •Интегрирование функций многих переменных
- •Свойствакратного интеграла
- •Контрольные вопросы к теме №10
- •Тема 11. Ряды Лекция 22. Ряды
- •Основные понятия
- •Положительные ряды
- •Знакочередующиеся ряды
- •Абсолютная сходимость
- •Функциональные ряды
- •Степенной ряд
- •Ряды Фурье
- •Ряды Фурье четных и нечетных функций
- •Понятие о рядах Фурье непериодических функций
- •Контрольные вопросы к теме №11
- •Тема 12. Дифференциальные уравнения Лекция 23. Дифференциальные уравнения
- •Основные понятия
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения семейства кривых
- •Геометрическое истолкование дифференциального уравнения
- •Задача Коши
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные дифференциальные уравнения
- •Метод Эйлера приближенного решения дифференциальных уравнений
- •Дифференциальные уравнения второго порядка
- •Задача Коши
- •Интегрируемые типы дифференциальных уравнений второго порядка
- •Случаи понижения порядка
- •Общие свойства решений линейных однородных дифференциальных уравнений второго порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
- •Линейные дифференциальные уравнения-го порядка
- •Контрольные вопросы к теме №12
- •Вопросы к экзамену
- •Литература
- •Высшая математика
- •220007, Г. Минск, ул. Московская, 17.
Монотонность функции
Функция
![]() называетсявозрастающейна промежутке
называетсявозрастающейна промежутке![]() ,
если
,
если![]() для любых точек
для любых точек![]() и
и![]() из промежутка
из промежутка![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству![]() .
Функция называетсяубывающейна
.
Функция называетсяубывающейна![]() ,
если из условия
,
если из условия![]() следует
следует![]() .
.
Теорема.Если функция
![]() непрерывна на отрезке
непрерывна на отрезке![]() ,
дифференцируема на интервале
,
дифференцируема на интервале![]() ,
то для того, чтобы
,
то для того, чтобы![]() была возрастающей (убывающей) необходимо
и достаточно, чтобы
была возрастающей (убывающей) необходимо
и достаточно, чтобы![]()
![]() в каждой внутренней точке интервала
в каждой внутренней точке интервала![]() .
.
Дифференцируемая
функция является возрастающей на
промежутке
![]() тогда и только тогда, когда
тогда и только тогда, когда![]() .
.
Пример.Найти промежутки возрастания и убывания
функции
![]() .
.
Вычислим:
![]() :
:![]() .
.
Точки
 делят числовую прямую
делят числовую прямую![]() на три интервала:
на три интервала: .
.
Производная
![]() положительна на интервалах
положительна на интервалах .
Следовательно, функция
.
Следовательно, функция![]() возрастает на каждом из этих интервалов.
На интервале
возрастает на каждом из этих интервалов.
На интервале производная
производная![]() неположительна, значит,
неположительна, значит,![]() убывает на этом интервале.
убывает на этом интервале.
Локальный экстремум
Точка
![]() называется точкойлокального
максимумафункции
называется точкойлокального
максимумафункции![]() ,
если существует интервал
,
если существует интервал![]() ,
содержащий точку
,
содержащий точку![]() такой что
такой что![]() .
.
Точка
![]() называется точкойлокального минимумафункции
называется точкойлокального минимумафункции![]() ,
если существует интервал
,
если существует интервал![]() ,
содержащий точку
,
содержащий точку![]() такой что
такой что![]() .
.
Точки локального минимума и локального максимума называются точками локального экстремума.
Необходимым
условием локального экстремума
дифференцируемой функции является
выполнение равенства
![]() .
Поэтому точки, в которых дифференцируемая
функция может иметь локальный экстремум,
находят, решая уравнение:
.
Поэтому точки, в которых дифференцируемая
функция может иметь локальный экстремум,
находят, решая уравнение:![]() .
.
Решения этого уравнения называют стационарными точками.
Исследование стационарных точек
I
правило.Если при возрастании![]() при переходе через стационарную точку
при переходе через стационарную точку![]() производная
производная![]() меняет знак с+на‑, то
меняет знак с+на‑, то![]() ‑ точка локального максимума. Если
‑ точка локального максимума. Если![]() меняет знак с‑на+, то
меняет знак с‑на+, то![]() ‑ точка локального минимума функции
‑ точка локального минимума функции![]() .
Если
.
Если![]() не меняет знак в точке
не меняет знак в точке![]() ,
то экстремума нет.
,
то экстремума нет.
II
правило.Если вторая производная![]() в стационарной точке
в стационарной точке![]() положительная, то
положительная, то![]() ‑ точка локального минимума функции
‑ точка локального минимума функции![]() .
Если вторая производная
.
Если вторая производная![]() в стационарной точке
в стационарной точке![]() отрицательная, то
отрицательная, то![]() ‑ точка локального максимума функции
‑ точка локального максимума функции![]() .
.
Точками локального экстремума функции могут быть такие точки, в которых производная не существует или обращается в бесконечность. Исследовать такие точки можно по Iправилу. Экстремум в такой точке называетсяострым экстремумом.
Пример.Найти экстремум функции
![]() .
.
 .
.
Функция
имеет стационарную точку
![]() (в этой точке производная равна нулю).
В точке
(в этой точке производная равна нулю).
В точке![]() производная обращается в бесконечность.
производная обращается в бесконечность.
Поскольку
![]() при
при![]() и
и![]() при
при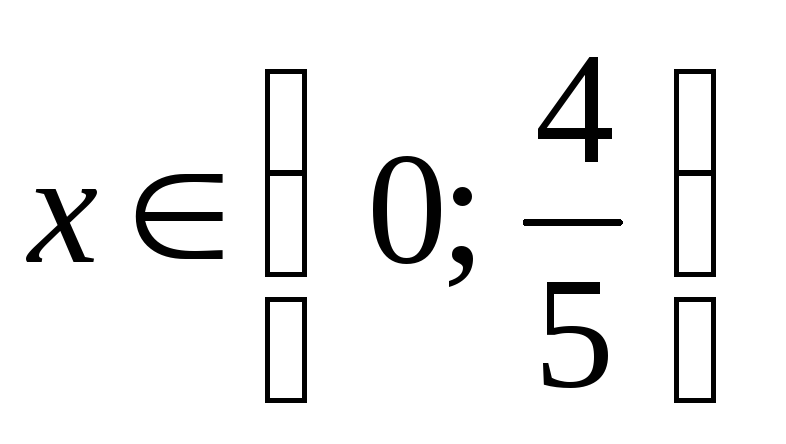 ,
то функция имеет в точке
,
то функция имеет в точке![]() локальный минимум
локальный минимум![]() .
Это будет острый минимум.
.
Это будет острый минимум.
При
переходе через стационарную точку
![]() производная меняет знак с‑на+, значит, функция имеет локальный
максимум
производная меняет знак с‑на+, значит, функция имеет локальный
максимум .
.
Глобальный экстремум
Непрерывная
на отрезке
![]() функция
функция![]() принимает свое наибольшее значение
принимает свое наибольшее значение![]() и свое наименьшее значение
и свое наименьшее значение![]() в точках этого отрезка. Эти значения
могут достигаться либо в стационарных
точках отрезка, либо в точках
недифференцируемости функции, либо в
граничных точках отрезка. Поэтому для
нахождения значений
в точках этого отрезка. Эти значения
могут достигаться либо в стационарных
точках отрезка, либо в точках
недифференцируемости функции, либо в
граничных точках отрезка. Поэтому для
нахождения значений![]() и
и![]() поступают следующим образом.
поступают следующим образом.
Находят стационарные точки
 функции;
функции;Находят точки
 ,
в которых производная
,
в которых производная не существует или обращается в
бесконечность;
не существует или обращается в
бесконечность;Вычисляют значения:
![]() ‑и выбирают
среди этих чисел наибольшее и наименьшее.
‑и выбирают
среди этих чисел наибольшее и наименьшее.
Это
и будут
![]() и
и![]() ‑ глобальные экстремальные значения.
‑ глобальные экстремальные значения.
Пример.Найти наибольшее и наименьшее значения
функции
![]() на отрезке
на отрезке![]() .
.
![]() ;
;
![]() .
.
Вычисляем
![]() .
Получаем числа
.
Получаем числа![]() .
Следовательно,
.
Следовательно,![]() ,
,![]() .
.
Выпуклость и перегибы графика функции
Графиком
функции![]() ,
заданной на множестве
,
заданной на множестве![]() ,
называют множество точек плоскости с
координатами
,
называют множество точек плоскости с
координатами![]() .
График называютвыпуклым внизна промежутке
.
График называютвыпуклым внизна промежутке![]() ,
если касательная к графику в любой точке
этого промежутка расположена ниже
графика. Если касательная расположена
выше графика, то график называютвыпуклым
вверх. Точка, в которой график меняет
направление выпуклости, называетсяточкой перегиба.
,
если касательная к графику в любой точке
этого промежутка расположена ниже
графика. Если касательная расположена
выше графика, то график называютвыпуклым
вверх. Точка, в которой график меняет
направление выпуклости, называетсяточкой перегиба.
Если
на промежутке
![]() вторая производная
вторая производная![]() положительна, то график является выпуклым
вниз на этом промежутке. Если
положительна, то график является выпуклым
вниз на этом промежутке. Если![]() на промежутке
на промежутке![]() ,
то график является выпуклым вверх на
промежутке
,
то график является выпуклым вверх на
промежутке![]() .
.
Точка
![]() может быть точкой перегиба только в том
случае, когда
может быть точкой перегиба только в том
случае, когда![]() ,
либо
,
либо![]() не существует – необходимое условие
перегиба. Однако равенство нулю или не
существование второй производной в
точке
не существует – необходимое условие
перегиба. Однако равенство нулю или не
существование второй производной в
точке![]() не означает еще, что в точке
не означает еще, что в точке![]() будет перегиб графика. Поэтому нужно
дополнительно исследовать такие точки.
будет перегиб графика. Поэтому нужно
дополнительно исследовать такие точки.
I
правило.Если![]() равна нулю или не существует и
равна нулю или не существует и![]() при переводе через точку
при переводе через точку![]() меняет
знак, то
меняет
знак, то![]() ‑ точка перегиба графика функции
‑ точка перегиба графика функции![]() .
.
II
правило.Если![]() и
и![]() ,
то
,
то![]() является точкой перегиба графика функции
является точкой перегиба графика функции![]() .
.
Пример.Найти промежутки выпуклости и точки
перегиба графика функции
![]() .
.
Вычислим
вторую производную
![]() .
.
![]() ;
;
![]() .
.
Точки
![]() и
и![]() разбивают числовую прямую на три
промежутка:
разбивают числовую прямую на три
промежутка:![]() .
На промежутках
.
На промежутках![]()
![]() вторая производная положительна,
на промежутке
вторая производная положительна,
на промежутке![]() ‑ отрицательна. Следовательно, график
функции является выпуклым вниз на
‑ отрицательна. Следовательно, график
функции является выпуклым вниз на![]() и выпуклым вверх на
и выпуклым вверх на![]() .
.
В
точках
![]() вторая производная равна нулю. Вычислим
вторая производная равна нулю. Вычислим![]() :
:![]() .
Поскольку
.
Поскольку![]() и
и![]() ,
то в точке
,
то в точке![]() ,и в точке
,и в точке![]() график функции имеет перегиб.
график функции имеет перегиб.
