
- •Академия управления при Президенте Республики Беларусь
- •Содержание
- •Тема 4. Функции 9
- •Тема 5. Дифференциальное исчисление функций одной переменной 34
- •Тема 6. Исследование функций 45
- •Тема 7. Пространство 66
- •Тема 8. Неопределенные интегралы 100
- •Тема 9. Определенные интегралы 114
- •Тема 10. Понятие кратного интеграла 132
- •Тема 11. Ряды 140
- •Тема 12. Дифференциальные уравнения 171
- •Тема 4. Функции Лекция 15. Функции
- •Основные понятия
- •Понятие числовой последовательности
- •Сходящиеся последовательности
- •Бесконечный предел
- •Замечательные пределы
- •Принцип сходимости
- •Предел функции. Теорема Гейне
- •Односторонние пределы
- •Пределы на бесконечности
- •Бесконечные пределы
- •Непрерывность функции
- •Непрерывность композиции
- •Точки разрыва
- •Контрольные вопросы к теме №4
- •Тема 5. Дифференциальное исчисление функций одной переменной Лекция 16. Дифференциальное исчисление функций одной переменной
- •Определение и смысл производной
- •Построение касательной к графику функции
- •Экономический смысл производной
- •Эластичность функции
- •Дифференцируемость функции
- •Правила дифференцирования
- •Производная сложной функции
- •Производная обратной функции
- •Дифференциал
- •Приближенные вычисления
- •Свойства дифференцируемых функций
- •Правила Лопиталя
- •Монотонность функции
- •Локальный экстремум
- •Исследование стационарных точек
- •Глобальный экстремум
- •Выпуклость и перегибы графика функции
- •Исследование функции и построение графика
- •Интерполяция и аппроксимация функций
- •Интерполяционный полином Лагранжа
- •Формула Тейлора
- •Основные разложения
- •Понятие об эмпирических формулах
- •Контрольные вопросы к теме №6
- •Тема 7. Пространство Лекция 18. Пространство
- •Точки, расстояние. Множества в
- •Последовательности в. Сходимость
- •Функции в. Предел. Теорема Гейне
- •Непрерывность функции в
- •Непрерывность на множестве
- •Теоремы о непрерывности
- •Дифференцируемость функций в. Частные производные
- •Дифференциал функции нескольких переменных
- •Необходимые условия дифференцируемости. Достаточные условия
- •Дифференцирование функции, заданной неявно и композиции функций
- •Полные дифференциалы и частные производные высших порядков. Признак полного дифференциала
- •Формула Тейлора
- •Локальный экстремум функции нескольких переменных. Необходимое и достаточное условия. Исследование стационарных точек
- •Условный экстремум функций нескольких переменных. Глобальный экстремум
- •Метод наименьших квадратов
- •Контрольные вопросы к теме №7
- •Свойства неопределенного интеграла
- •Замена переменных
- •Интегрирование по частям
- •Интегрирование рациональных функций. Метод рационализации
- •Вычисление
- •Вычисление
- •Вычисление
- •Вычисление
- •Контрольные вопросы к теме №8
- •Тема 9. Определенные интегралы Лекция 20. Определенные интегралы
- •Интегральные суммы
- •Необходимое и достаточное условие интегрируемости
- •Равномерно непрерывные функции
- •Интегрируемость непрерывных, разрывных и монотонных функций
- •Основные свойства определенного интеграла
- •Оценки интегралов. Формулы среднего значения
- •Основные правила интегрирования
- •Приложения определенного интеграла Площадь плоской фигуры
- •. Объемы тел вращения
- •Несобственные интегралы
- •Интегрирование неограниченных функций
- •Интегрирование по бесконечному промежутку
- •Приближенное вычисление определенных интегралов
- •Формула прямоугольников
- •Формула трапеций
- •Контрольные вопросы к теме №9
- •Тема 10. Понятие кратного интеграла Лекция 21. Понятие кратного интеграла
- •Интегрирование функций многих переменных
- •Свойствакратного интеграла
- •Контрольные вопросы к теме №10
- •Тема 11. Ряды Лекция 22. Ряды
- •Основные понятия
- •Положительные ряды
- •Знакочередующиеся ряды
- •Абсолютная сходимость
- •Функциональные ряды
- •Степенной ряд
- •Ряды Фурье
- •Ряды Фурье четных и нечетных функций
- •Понятие о рядах Фурье непериодических функций
- •Контрольные вопросы к теме №11
- •Тема 12. Дифференциальные уравнения Лекция 23. Дифференциальные уравнения
- •Основные понятия
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения семейства кривых
- •Геометрическое истолкование дифференциального уравнения
- •Задача Коши
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные дифференциальные уравнения
- •Метод Эйлера приближенного решения дифференциальных уравнений
- •Дифференциальные уравнения второго порядка
- •Задача Коши
- •Интегрируемые типы дифференциальных уравнений второго порядка
- •Случаи понижения порядка
- •Общие свойства решений линейных однородных дифференциальных уравнений второго порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
- •Линейные дифференциальные уравнения-го порядка
- •Контрольные вопросы к теме №12
- •Вопросы к экзамену
- •Литература
- •Высшая математика
- •220007, Г. Минск, ул. Московская, 17.
Дифференциальные уравнения первого порядка
Дифференциальным уравнением первого порядканазывается уравнение вида:
|
|
(2) |
где
![]() ‑ аргумент;
‑ аргумент;![]() ‑ неизвестная функция.
‑ неизвестная функция.
Наиболее
простым является дифференциальное
уравнение, разрешенное относительно
![]() :
:![]() .
.
Иногда уравнение первого порядка записывается в форме:
![]() .
.
Функция
![]() называется решением уравнения (1), если
она обращает его в тождество, т.е.
называется решением уравнения (1), если
она обращает его в тождество, т.е.![]() .
.
Решение,
заданное неявно, т.е. в виде
![]() ,
называетсяинтеграломдифференциального уравнения.
,
называетсяинтеграломдифференциального уравнения.
Пример.Показать, что уравнение
![]() ,
определяющее
,
определяющее![]() ,
как неявную функцию от
,
как неявную функцию от![]() ,
есть интеграл дифференциального
уравнения
,
есть интеграл дифференциального
уравнения![]() .
.
Дифференцируя
данное уравнение, найдем
![]() :
:
![]() .
.
Подставив
![]() в дифференциальное уравнение, получим
тождество:
в дифференциальное уравнение, получим
тождество:
![]() .
.
Дифференциальные уравнения семейства кривых
Однопараметрическим
семейством кривыхназывается
совокупность линий, определяемая
уравнением![]() .
Фиксируя значение параметра
.
Фиксируя значение параметра![]() ,
получают конкретную линию данного
семейства. Например, уравнение
,
получают конкретную линию данного
семейства. Например, уравнение![]() определяет собой семейство парабол с
вершиной в начале координат, симметричных
относительно оси
определяет собой семейство парабол с
вершиной в начале координат, симметричных
относительно оси![]() .
Придавая параметру
.
Придавая параметру![]() значения, получают параболы
значения, получают параболы![]() .
.
Дифференцируя
уравнение семейства линий по
![]() (считая
(считая![]() функцией от
функцией от![]() ):
):![]() и исключая параметр
и исключая параметр![]() ,
приходят к дифференциальному уравнению
вида
,
приходят к дифференциальному уравнению
вида![]() ,
которому удовлетворяет любая линия
данного семейства.
,
которому удовлетворяет любая линия
данного семейства.
Пример.Из семейства окружностей
![]() выделить ту, которая проходит через
точку
выделить ту, которая проходит через
точку![]() .
Составить дифференциальное уравнение
данного семейства окружностей.
.
Составить дифференциальное уравнение
данного семейства окружностей.
Чтобы
выделить нужную окружность, необходимо
найти соответствующее ей значение
параметра
![]() .
Так как искомая окружность проходит
через точку
.
Так как искомая окружность проходит
через точку![]() ,
то координаты этой точки удовлетворяют
уравнению окружности. Подставляя
,
то координаты этой точки удовлетворяют
уравнению окружности. Подставляя![]() ,
получим
,
получим![]() .
Искомое уравнение имеет вид:
.
Искомое уравнение имеет вид:![]() .
.
Чтобы
составить дифференциальное уравнение
семейства окружностей
![]() ,
продифференцируем его по
,
продифференцируем его по![]() :
:![]() или
или![]() .
.
Геометрическое истолкование дифференциального уравнения
Пусть
![]() является решением дифференциального
уравнения
является решением дифференциального
уравнения![]() .
График функции
.
График функции![]() называетсяинтегральной кривойуравнения. Само дифференциальное
уравнение устанавливает зависимость
между координатами точки
называетсяинтегральной кривойуравнения. Само дифференциальное
уравнение устанавливает зависимость
между координатами точки![]() и угловым коэффициентом касательной
и угловым коэффициентом касательной![]() к интегральной кривой в той же точке.
к интегральной кривой в той же точке.
Если
через
![]() обозначить угол между касательной и
интегральной кривой в точке
обозначить угол между касательной и
интегральной кривой в точке![]() и положительным направлением оси
и положительным направлением оси![]() ,
то
,
то![]() ,
а
,
а![]() ,
следовательно,
,
следовательно,![]() .
Это означает, что направление касательных
к интегральным кривым задается самим
дифференциальным уравнением.
.
Это означает, что направление касательных
к интегральным кривым задается самим
дифференциальным уравнением.
Геометрически
уравнение
![]() равносильно заданию в области определения
функции
равносильно заданию в области определения
функции![]() поля направлений, а интегрирование
этого уравнения равносильно проведению
таких линий, которые в каждой своей
точке касаются направления поля,
заданного в этой точке.
поля направлений, а интегрирование
этого уравнения равносильно проведению
таких линий, которые в каждой своей
точке касаются направления поля,
заданного в этой точке.
Изучая
поле направлений, определяемое данным
дифференциальным уравнением, получают
некоторое представление об интегральных
кривых этого уравнения, а иногда и сами
интегральные кривые. Линия, вдоль которой
направление поля, определяемого
уравнением
![]() одно и то же, называетсяизоклиной.
Уравнение изоклины получается из
уравнения
одно и то же, называетсяизоклиной.
Уравнение изоклины получается из
уравнения![]() ,
если положить
,
если положить![]() ,
т.е.
,
т.е.![]() .
.
Пример.Изоклинами уравнения
![]() является семейство окружностей.
является семейство окружностей.
Задача Коши
Задача
Кошидля дифференциального уравнения
первого порядка состоит в том, чтобы
найти решение, которое при заданном
значении аргумента![]() принимает заданное значение
принимает заданное значение![]() ,
т.е. удовлетворяет начальному условию
,
т.е. удовлетворяет начальному условию![]() .
.
Геометрически
задача Коши формулируется следующим
образом: среди всех интегральных
кривых данного дифференциального
уравнения выделить ту, которая проходит
через заданную точку
![]() .Решение задачи Коши называютчастным
решением дифференциального уравнения.
.Решение задачи Коши называютчастным
решением дифференциального уравнения.
Пример.Найти:
семейство кривых, для которых угловой коэффициент касательной равен ординате точки касания;
кривую этого семейства, проходящую через точку
 .
.
Решение.
Дифференциальное
уравнение искомого семейства
![]() или
или![]() .
.
Проинтегрировав
обе части равенства, получим:
![]() ,
откуда
,
откуда![]() ‑ уравнение семейства кривых,
обладающих заданным свойством.
‑ уравнение семейства кривых,
обладающих заданным свойством.
Определим
значение
![]() ,
соответствующее начальным значениям:
,
соответствующее начальным значениям:![]() ,
т.е.
,
т.е.![]() .
.
Следовательно,
![]() ‑ искомая интегральная кривая.
‑ искомая интегральная кривая.
Дифференциальное
уравнение
![]() –го
порядка можно свести к системе
–го
порядка можно свести к системе![]() дифференциальных уравнений 1-го порядка.
В самом деле, если обозначить
дифференциальных уравнений 1-го порядка.
В самом деле, если обозначить![]() через
через![]() ,
,![]() через
через![]() ,…,
,…,![]() через
через![]() ,
получим систему дифференциальных
уравнений:
,
получим систему дифференциальных
уравнений:

Для
этой системы также можно ввести понятия
частного и общего решений, а также
начальных условий. Начальные условия
можно задавать значениями всех функций
![]() в некоторой точке
в некоторой точке![]() ,
т.е. это просто начальные условия
исходного уравнения
,
т.е. это просто начальные условия
исходного уравнения![]() –го
порядка. Когда такое решение будет
найдено, то функция
–го
порядка. Когда такое решение будет
найдено, то функция![]() будет искомым частным решением исходного
уравнения
будет искомым частным решением исходного
уравнения![]() –го
порядка. Верно и обратное: если дана
произвольная система дифференциальных
уравнений первого порядка, то, исключив
из нее все неизвестные функции, кроме
одной, ее можно свести к одному уравнению
соответствующего порядка, которое,
возможно, проще решить.
–го
порядка. Верно и обратное: если дана
произвольная система дифференциальных
уравнений первого порядка, то, исключив
из нее все неизвестные функции, кроме
одной, ее можно свести к одному уравнению
соответствующего порядка, которое,
возможно, проще решить.
Пример.Решить систему двух уравнений первого порядка:

Решение.Продифференцировав первое уравнение,
получим![]() .
Подставим в него
.
Подставим в него![]() из второго уравнения, получим
из второго уравнения, получим![]() .
Общее решение этого уравнения имеет
вид
.
Общее решение этого уравнения имеет
вид![]() .
Используя первое уравнение, получаем
.
Используя первое уравнение, получаем![]() ,
и исходная система решена.
,
и исходная система решена.
Теперь рассмотрим систему дифференциальных уравнений первого порядка вида:
 ,
,
которую
коротко можно записать в векторной
форме
![]() .
.
Задача
Коши для такой системы формулируется
следующим образом: для заданной точки
![]() найти вектор-функцию
найти вектор-функцию![]() ,
которая является решением системы
уравнений и
,
которая является решением системы
уравнений и![]() .
.
Рассмотрим
задачу Коши для разрешенного относительно
![]() дифференциального уравнения
дифференциального уравнения![]() –го
порядка
–го
порядка![]() ,
которое можно получить из рассмотренной
выше системы дифференциальных уравнений
первого порядка, если ввести обозначения:
,
которое можно получить из рассмотренной
выше системы дифференциальных уравнений
первого порядка, если ввести обозначения:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
……………………
![]() ;
;
![]() ,
,
получится
эквивалентная система
![]() дифференциальных уравнений первого
порядка:
дифференциальных уравнений первого
порядка:
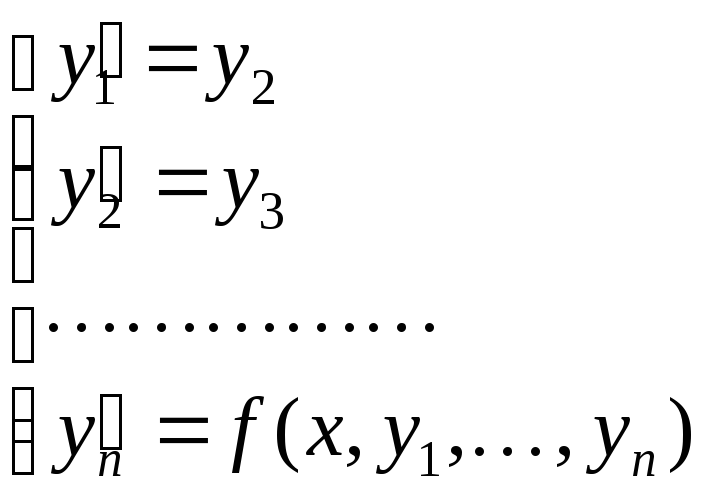
Задача
Коши для уравнения
![]() –го
порядка формулируется следующим образом:
найти решение уравнения
–го
порядка формулируется следующим образом:
найти решение уравнения![]() для данных значений:
для данных значений:

Точки
![]() и
и![]() называютсяначальными условиями,
их можно записать также в виде
называютсяначальными условиями,
их можно записать также в виде![]() и
и![]() .
.
Существование и единственность решения задачи Коши может быть сформулировано в виде следующих теорем.
Теорема.
Пусть в некоторой области
![]() функция
функция![]() и ее частная производная
и ее частная производная![]() непрерывны. Тогда через каждую точку
непрерывны. Тогда через каждую точку![]() проходит единственное решение
дифференциального уравнения
проходит единственное решение
дифференциального уравнения![]() .
.
Графически
это можно представить как семейство
кривых, представляющих графики решений,
которые полностью заполняют область
![]() ,
но при этом они не могут иметь общих
точек, т.е. они не пересекаются и не
касаются друг друга.
,
но при этом они не могут иметь общих
точек, т.е. они не пересекаются и не
касаются друг друга.

Теорема. Рассмотрим систему дифференциальных уравнений.
Если
функции
![]() и их частные производные по
и их частные производные по![]() непрерывны в
непрерывны в![]() –мерной
области
–мерной
области![]() ,
то через каждую точку
,
то через каждую точку![]() области
области![]() проходит единственное в области
проходит единственное в области![]() решение
решение![]() системы дифференциальных уравнений:
системы дифференциальных уравнений:
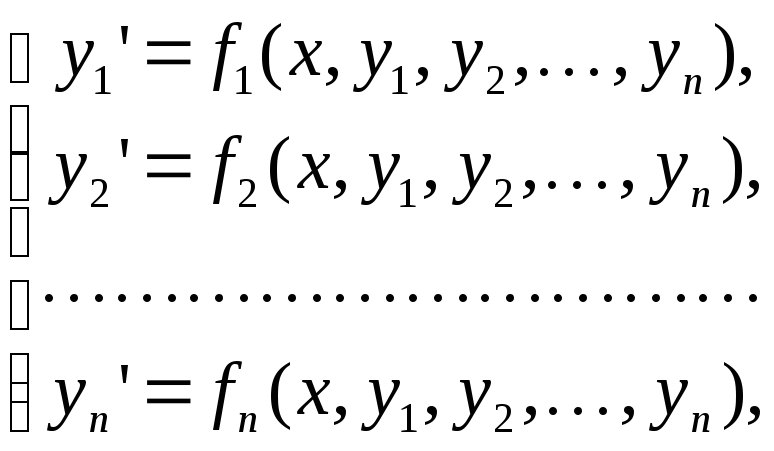
Теоремы существования и единственности решения задачи Коши позволяют описать множество решений дифференциального уравнения в виде общего решения.
