
- •Академия управления при Президенте Республики Беларусь
- •Содержание
- •Тема 4. Функции 9
- •Тема 5. Дифференциальное исчисление функций одной переменной 34
- •Тема 6. Исследование функций 45
- •Тема 7. Пространство 66
- •Тема 8. Неопределенные интегралы 100
- •Тема 9. Определенные интегралы 114
- •Тема 10. Понятие кратного интеграла 132
- •Тема 11. Ряды 140
- •Тема 12. Дифференциальные уравнения 171
- •Тема 4. Функции Лекция 15. Функции
- •Основные понятия
- •Понятие числовой последовательности
- •Сходящиеся последовательности
- •Бесконечный предел
- •Замечательные пределы
- •Принцип сходимости
- •Предел функции. Теорема Гейне
- •Односторонние пределы
- •Пределы на бесконечности
- •Бесконечные пределы
- •Непрерывность функции
- •Непрерывность композиции
- •Точки разрыва
- •Контрольные вопросы к теме №4
- •Тема 5. Дифференциальное исчисление функций одной переменной Лекция 16. Дифференциальное исчисление функций одной переменной
- •Определение и смысл производной
- •Построение касательной к графику функции
- •Экономический смысл производной
- •Эластичность функции
- •Дифференцируемость функции
- •Правила дифференцирования
- •Производная сложной функции
- •Производная обратной функции
- •Дифференциал
- •Приближенные вычисления
- •Свойства дифференцируемых функций
- •Правила Лопиталя
- •Монотонность функции
- •Локальный экстремум
- •Исследование стационарных точек
- •Глобальный экстремум
- •Выпуклость и перегибы графика функции
- •Исследование функции и построение графика
- •Интерполяция и аппроксимация функций
- •Интерполяционный полином Лагранжа
- •Формула Тейлора
- •Основные разложения
- •Понятие об эмпирических формулах
- •Контрольные вопросы к теме №6
- •Тема 7. Пространство Лекция 18. Пространство
- •Точки, расстояние. Множества в
- •Последовательности в. Сходимость
- •Функции в. Предел. Теорема Гейне
- •Непрерывность функции в
- •Непрерывность на множестве
- •Теоремы о непрерывности
- •Дифференцируемость функций в. Частные производные
- •Дифференциал функции нескольких переменных
- •Необходимые условия дифференцируемости. Достаточные условия
- •Дифференцирование функции, заданной неявно и композиции функций
- •Полные дифференциалы и частные производные высших порядков. Признак полного дифференциала
- •Формула Тейлора
- •Локальный экстремум функции нескольких переменных. Необходимое и достаточное условия. Исследование стационарных точек
- •Условный экстремум функций нескольких переменных. Глобальный экстремум
- •Метод наименьших квадратов
- •Контрольные вопросы к теме №7
- •Свойства неопределенного интеграла
- •Замена переменных
- •Интегрирование по частям
- •Интегрирование рациональных функций. Метод рационализации
- •Вычисление
- •Вычисление
- •Вычисление
- •Вычисление
- •Контрольные вопросы к теме №8
- •Тема 9. Определенные интегралы Лекция 20. Определенные интегралы
- •Интегральные суммы
- •Необходимое и достаточное условие интегрируемости
- •Равномерно непрерывные функции
- •Интегрируемость непрерывных, разрывных и монотонных функций
- •Основные свойства определенного интеграла
- •Оценки интегралов. Формулы среднего значения
- •Основные правила интегрирования
- •Приложения определенного интеграла Площадь плоской фигуры
- •. Объемы тел вращения
- •Несобственные интегралы
- •Интегрирование неограниченных функций
- •Интегрирование по бесконечному промежутку
- •Приближенное вычисление определенных интегралов
- •Формула прямоугольников
- •Формула трапеций
- •Контрольные вопросы к теме №9
- •Тема 10. Понятие кратного интеграла Лекция 21. Понятие кратного интеграла
- •Интегрирование функций многих переменных
- •Свойствакратного интеграла
- •Контрольные вопросы к теме №10
- •Тема 11. Ряды Лекция 22. Ряды
- •Основные понятия
- •Положительные ряды
- •Знакочередующиеся ряды
- •Абсолютная сходимость
- •Функциональные ряды
- •Степенной ряд
- •Ряды Фурье
- •Ряды Фурье четных и нечетных функций
- •Понятие о рядах Фурье непериодических функций
- •Контрольные вопросы к теме №11
- •Тема 12. Дифференциальные уравнения Лекция 23. Дифференциальные уравнения
- •Основные понятия
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения семейства кривых
- •Геометрическое истолкование дифференциального уравнения
- •Задача Коши
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные дифференциальные уравнения
- •Метод Эйлера приближенного решения дифференциальных уравнений
- •Дифференциальные уравнения второго порядка
- •Задача Коши
- •Интегрируемые типы дифференциальных уравнений второго порядка
- •Случаи понижения порядка
- •Общие свойства решений линейных однородных дифференциальных уравнений второго порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
- •Линейные дифференциальные уравнения-го порядка
- •Контрольные вопросы к теме №12
- •Вопросы к экзамену
- •Литература
- •Высшая математика
- •220007, Г. Минск, ул. Московская, 17.
Ряды Фурье четных и нечетных функций
Рассмотрим симметричный интеграл:

где
![]() –
функция, непрерывная или кусочно–непрерывная
на отрезке
–
функция, непрерывная или кусочно–непрерывная
на отрезке![]() .
.
Делая
в первом интеграле подстановку
![]() ,
,![]() и учитывая независимость определенного
интеграла от обозначения переменной
интегрирования, получим:
и учитывая независимость определенного
интеграла от обозначения переменной
интегрирования, получим:


Пусть функция
 –
четная, т.е.
–
четная, т.е. .
Тогда:
.
Тогда:
 .
.
Таким образом, симметричный интеграл от четной функции равен удвоенному интегралу от этой функции, взятому по половинному промежутку интегрирования.
Пусть функция
 –
нечетная, т.е.
–
нечетная, т.е.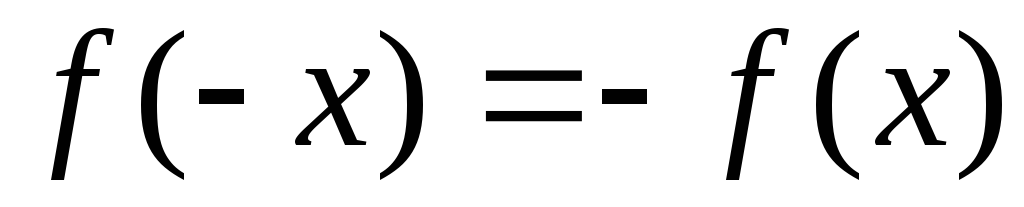 .
Тогда:
.
Тогда: .
.
Таким образом, симметричный интеграл от нечетной функции равен нулю.
Теорема.
Ряд Фурье четной периодической функции содержит только косинусы кратных дуг, т.е. в его состав входят только четные гармоники, включая свободный член;
Ряд Фурье нечетной периодической функции содержит только синусы кратных дуг, т.е. в его состав входят только нечетные гармоники.
Доказательство:
Пусть функция
 –
четная и периодическая с периодом
–
четная и периодическая с периодом ,
а
,
а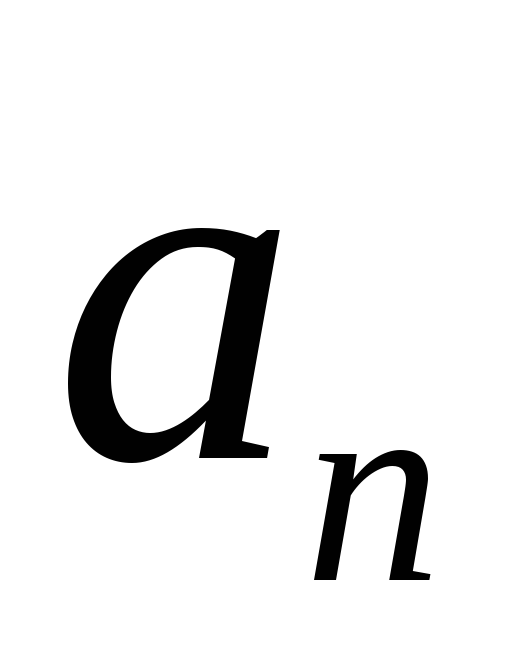 и
и – ее коэффициенты. На основании формулы
для вычисления ее коэффициентов и
учитывая, что
– ее коэффициенты. На основании формулы
для вычисления ее коэффициентов и
учитывая, что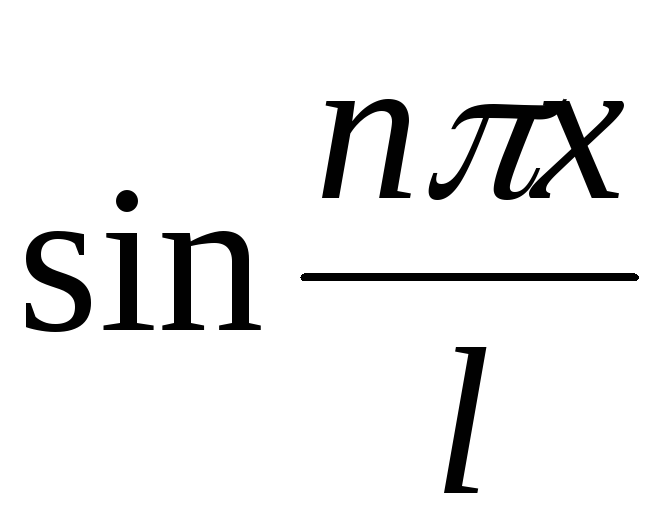
 – нечетные функции, имеем
– нечетные функции, имеем .
.
Поэтому
 ,
где:
,
где:
 .
.
Пусть функция
 –
нечетная и периодическая с периодом
–
нечетная и периодическая с периодом ,
а
,
а и
и – ее коэффициенты. На основании формулы
для вычисления ее коэффициентов и
учитывая, что
– ее коэффициенты. На основании формулы
для вычисления ее коэффициентов и
учитывая, что
 – четные функции, имеем
– четные функции, имеем .
.
Поэтому
 ,
где:
,
где:
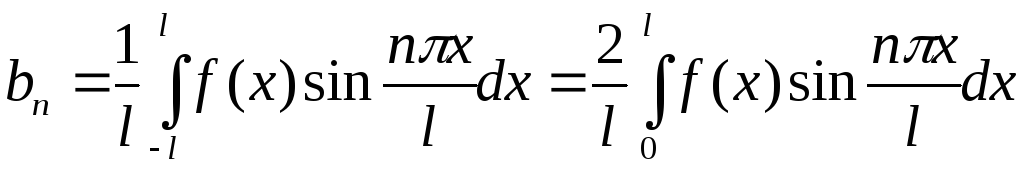
![]() .
.
Теорема доказана.
Понятие о рядах Фурье непериодических функций
Кусочно-дифференцируемую
непериодическую функцию
![]() ,
заданную на бесконечной оси
,
заданную на бесконечной оси![]() ,
нельзя представить ее рядом Фурье, так
как его сумма, будучи суммой гармоник
с общим периодом
,
нельзя представить ее рядом Фурье, так
как его сумма, будучи суммой гармоник
с общим периодом![]() ,
есть функция периодическая с тем же
периодом и, следовательно, не может быть
равен функции
,
есть функция периодическая с тем же
периодом и, следовательно, не может быть
равен функции![]() для всех
для всех![]() .
Однако можно построить представление
этой функции в виде соответствующего
ряда Фурье на любом конечном промежутке.
.
Однако можно построить представление
этой функции в виде соответствующего
ряда Фурье на любом конечном промежутке.
Пусть
интересующий промежуток есть
![]() ,
т.е. симметричен относительно начала
координат (этого всегда можно добиться
параллельным сдвигом оси
,
т.е. симметричен относительно начала
координат (этого всегда можно добиться
параллельным сдвигом оси![]() ).
).
Построим
функцию
![]() периода
периода![]() такую, что
такую, что![]()
![]()
![]() при
при![]() .
.
Предполагая,
что функция
![]() удовлетворяет условиям теоремы о
сходимости, имеем:
удовлетворяет условиям теоремы о
сходимости, имеем:

![]() ,
где коэффициенты
,
где коэффициенты
![]() и
и![]() определяются по формулам:
определяются по формулам:

 .
.
Отсюда
на основании тождества
![]()
![]()
![]() получим:
получим:

![]() ,
где:
,
где:

 .
.
Теперь
необходимо подсчитать сумму ряда на
концевых точках
![]() .
.
Согласно общей формуле:

на
основании тождества между
![]() и
и![]() ,
а также
,
а также![]() периодичности
функции
периодичности
функции![]() очевидно, что
очевидно, что![]() ,
,
![]()
Таким образом, получается, что:

Из
![]() периодичности
функции
периодичности
функции![]() следует, что
следует, что![]() .
.
Пусть
теперь необходимо непериодическую
функцию
![]() представить в виде ряда Фурье периода
представить в виде ряда Фурье периода![]() на полупериоде
на полупериоде![]() .
.
Полагая
 ,
,
где
![]() – произвольная кусочно–дифференцируемая
функция, получаем бесконечное множество
рядов Фурье:
– произвольная кусочно–дифференцируемая
функция, получаем бесконечное множество
рядов Фурье:
 ,
(
,
(![]() ),
),
дающих
представление функции
![]() на
интервале
на
интервале![]() .
.
В
частности, полагая, что
![]() (
(![]() ),
т.е. что функция
),
т.е. что функция![]() – четная, получим:
– четная, получим:
 ,
(
,
(![]() ),
),
где
 .
.
Аналогично,
полагая, что
![]() (
(![]() ),
т.е. что функция
),
т.е. что функция![]() – нечетная, получим:
– нечетная, получим:
 ,
,
где

![]() .
.
Таким образом, кусочно–дифференцируемую функцию, заданную на полупериоде, можно разложить в соответствующий ряд Фурье бесчисленным множеством способов. В частности, по желанию эту функцию на данном полупериоде можно представить в виде суммы четных гармоник или в виде суммы нечетных гармоник.
Контрольные вопросы к теме №11
Понятия числового ряда и его сходимости.
Признаки сходимости ряда. Геометрический и гармонический ряды.
Знакопеременные и знакочередующиеся ряды, их сходимость и абсолютная сходимость.
Область сходимости функционального ряда. Понятие равномерной сходимости ряда.
Радиус сходимости степенного ряда, основные методы его определения.
Ряд Тейлора. Разложение функций в ряд Тейлора.
Понятие кусочно-дифференцируемой функции.
Понятие ортогональности функций.
Ряд Фурье. Понятие гармонического анализа.
