
- •Академия управления при Президенте Республики Беларусь
- •Содержание
- •Тема 4. Функции 9
- •Тема 5. Дифференциальное исчисление функций одной переменной 34
- •Тема 6. Исследование функций 45
- •Тема 7. Пространство 66
- •Тема 8. Неопределенные интегралы 100
- •Тема 9. Определенные интегралы 114
- •Тема 10. Понятие кратного интеграла 132
- •Тема 11. Ряды 140
- •Тема 12. Дифференциальные уравнения 171
- •Тема 4. Функции Лекция 15. Функции
- •Основные понятия
- •Понятие числовой последовательности
- •Сходящиеся последовательности
- •Бесконечный предел
- •Замечательные пределы
- •Принцип сходимости
- •Предел функции. Теорема Гейне
- •Односторонние пределы
- •Пределы на бесконечности
- •Бесконечные пределы
- •Непрерывность функции
- •Непрерывность композиции
- •Точки разрыва
- •Контрольные вопросы к теме №4
- •Тема 5. Дифференциальное исчисление функций одной переменной Лекция 16. Дифференциальное исчисление функций одной переменной
- •Определение и смысл производной
- •Построение касательной к графику функции
- •Экономический смысл производной
- •Эластичность функции
- •Дифференцируемость функции
- •Правила дифференцирования
- •Производная сложной функции
- •Производная обратной функции
- •Дифференциал
- •Приближенные вычисления
- •Свойства дифференцируемых функций
- •Правила Лопиталя
- •Монотонность функции
- •Локальный экстремум
- •Исследование стационарных точек
- •Глобальный экстремум
- •Выпуклость и перегибы графика функции
- •Исследование функции и построение графика
- •Интерполяция и аппроксимация функций
- •Интерполяционный полином Лагранжа
- •Формула Тейлора
- •Основные разложения
- •Понятие об эмпирических формулах
- •Контрольные вопросы к теме №6
- •Тема 7. Пространство Лекция 18. Пространство
- •Точки, расстояние. Множества в
- •Последовательности в. Сходимость
- •Функции в. Предел. Теорема Гейне
- •Непрерывность функции в
- •Непрерывность на множестве
- •Теоремы о непрерывности
- •Дифференцируемость функций в. Частные производные
- •Дифференциал функции нескольких переменных
- •Необходимые условия дифференцируемости. Достаточные условия
- •Дифференцирование функции, заданной неявно и композиции функций
- •Полные дифференциалы и частные производные высших порядков. Признак полного дифференциала
- •Формула Тейлора
- •Локальный экстремум функции нескольких переменных. Необходимое и достаточное условия. Исследование стационарных точек
- •Условный экстремум функций нескольких переменных. Глобальный экстремум
- •Метод наименьших квадратов
- •Контрольные вопросы к теме №7
- •Свойства неопределенного интеграла
- •Замена переменных
- •Интегрирование по частям
- •Интегрирование рациональных функций. Метод рационализации
- •Вычисление
- •Вычисление
- •Вычисление
- •Вычисление
- •Контрольные вопросы к теме №8
- •Тема 9. Определенные интегралы Лекция 20. Определенные интегралы
- •Интегральные суммы
- •Необходимое и достаточное условие интегрируемости
- •Равномерно непрерывные функции
- •Интегрируемость непрерывных, разрывных и монотонных функций
- •Основные свойства определенного интеграла
- •Оценки интегралов. Формулы среднего значения
- •Основные правила интегрирования
- •Приложения определенного интеграла Площадь плоской фигуры
- •. Объемы тел вращения
- •Несобственные интегралы
- •Интегрирование неограниченных функций
- •Интегрирование по бесконечному промежутку
- •Приближенное вычисление определенных интегралов
- •Формула прямоугольников
- •Формула трапеций
- •Контрольные вопросы к теме №9
- •Тема 10. Понятие кратного интеграла Лекция 21. Понятие кратного интеграла
- •Интегрирование функций многих переменных
- •Свойствакратного интеграла
- •Контрольные вопросы к теме №10
- •Тема 11. Ряды Лекция 22. Ряды
- •Основные понятия
- •Положительные ряды
- •Знакочередующиеся ряды
- •Абсолютная сходимость
- •Функциональные ряды
- •Степенной ряд
- •Ряды Фурье
- •Ряды Фурье четных и нечетных функций
- •Понятие о рядах Фурье непериодических функций
- •Контрольные вопросы к теме №11
- •Тема 12. Дифференциальные уравнения Лекция 23. Дифференциальные уравнения
- •Основные понятия
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения семейства кривых
- •Геометрическое истолкование дифференциального уравнения
- •Задача Коши
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные дифференциальные уравнения
- •Метод Эйлера приближенного решения дифференциальных уравнений
- •Дифференциальные уравнения второго порядка
- •Задача Коши
- •Интегрируемые типы дифференциальных уравнений второго порядка
- •Случаи понижения порядка
- •Общие свойства решений линейных однородных дифференциальных уравнений второго порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
- •Линейные дифференциальные уравнения-го порядка
- •Контрольные вопросы к теме №12
- •Вопросы к экзамену
- •Литература
- •Высшая математика
- •220007, Г. Минск, ул. Московская, 17.
Степенной ряд
Степенным рядомназывается ряд вида:
|
|
(9) |
где
![]() ‑ числовые коэффициенты,
‑ числовые коэффициенты,![]() ‑ фиксированное число и
‑ фиксированное число и![]() ‑ переменная.
‑ переменная.
Если
зафиксировать
![]() ,
то получится числовой ряд. Если этот
числовой ряд сходится, то говорят, что
степенной ряд (9) сходится в точке
,
то получится числовой ряд. Если этот
числовой ряд сходится, то говорят, что
степенной ряд (9) сходится в точке![]() .
Множество всех точек
.
Множество всех точек![]() ,
в которых ряд (9) сходится, называютмножеством сходимостиряда (9).
,
в которых ряд (9) сходится, называютмножеством сходимостиряда (9).
Пример.Ряд
![]() сходится
абсолютно при
сходится
абсолютно при![]() ,
т.к.
,
т.к.![]() при
при![]() сходится. Если же
сходится. Если же![]() ,
то
,
то![]() не стремится к нулю, т.е. не выполнено
необходимое условие сходимости и ряд
расходится. Таким образом, множеством
сходимости ряда
не стремится к нулю, т.е. не выполнено
необходимое условие сходимости и ряд
расходится. Таким образом, множеством
сходимости ряда![]() является
является![]() .
.
Множество
сходимости всякого ряда (9) есть промежуток,
середина которого находится в точке
![]() .
Промежуток сходимости может быть
отрезком, полуинтервалом, интервалом,
бесконечным промежутком или промежутком
нулевой длины, т.е. точкой
.
Промежуток сходимости может быть
отрезком, полуинтервалом, интервалом,
бесконечным промежутком или промежутком
нулевой длины, т.е. точкой![]() .
Число
.
Число![]() ,
равное половине длины промежутка
сходимости, называютрадиусом
сходимости. Радиус сходимости ряда
(9) может быть вычислен следующим образом:
,
равное половине длины промежутка
сходимости, называютрадиусом
сходимости. Радиус сходимости ряда
(9) может быть вычислен следующим образом:
 ,
если такой предел существует;
,
если такой предел существует; ,
если такой предел существует.
,
если такой предел существует.
Если
в формулах 2. и 3. пределы равны 0, то
![]() .
Если пределы равны
.
Если пределы равны![]() ,
то
,
то![]() .
.
Если
![]() ‑ конечное число, то промежуток
‑ конечное число, то промежуток![]() принадлежит множеству сходимости. В
ряде случаев множеству сходимости могут
принадлежать также точки
принадлежит множеству сходимости. В
ряде случаев множеству сходимости могут
принадлежать также точки![]() и
и![]() .
.
Пример.Ряд
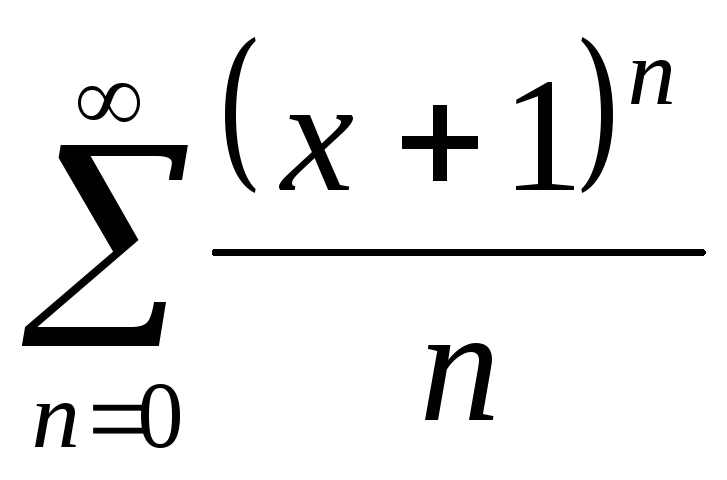 имеет радиус сходимости
имеет радиус сходимости .
.
Значит,
интервал
![]() входит в промежуток сходимости. Исследуем
сходимость ряда на концах интервала
входит в промежуток сходимости. Исследуем
сходимость ряда на концах интервала![]() .
При
.
При![]() получаем ряд
получаем ряд ,
который сходится по признаку Лейбница.
При
,
который сходится по признаку Лейбница.
При![]() получаем ряд
получаем ряд![]() ,
который расходится. Таким образом,
промежуток сходимости ряда – полуинтервал
,
который расходится. Таким образом,
промежуток сходимости ряда – полуинтервал![]() .
.
Пример.Ряд
 имеет радиус сходимости
имеет радиус сходимости .Значит, интервал сходимости
.Значит, интервал сходимости![]() .
.
Изучим
сходимость ряда на концах этого интервала.
При
![]() получаем ряд
получаем ряд ,
который сходится абсолютно. При
,
который сходится абсолютно. При![]() получаем ряд
получаем ряд![]() ,
который также сходится. Значит, промежуток
сходимости – отрезок
,
который также сходится. Значит, промежуток
сходимости – отрезок![]() .
.
Если
функция
![]() в точке
в точке![]() имеет производные любого порядка, то
для нее можно построить степенной ряд:
имеет производные любого порядка, то
для нее можно построить степенной ряд:
|
|
(10) |
Этот
ряд называется рядом Тейлорадля
функции![]() в точке
в точке![]() .
.
Множество
сходимости ряда (10) не всегда совпадает
с областью определения функции
![]() ,
а его сумма не обязательно равна
,
а его сумма не обязательно равна![]() .
Если сумма ряда (10) совпадает с
.
Если сумма ряда (10) совпадает с![]() на множестве
на множестве![]() ,
то можно написать:
,
то можно написать:
|
|
(11) |
В
этом случае говорят, что
![]() на множестве
на множестве![]() разложена в степенной ряд
(11). Справедливы следующие разложения:
разложена в степенной ряд
(11). Справедливы следующие разложения:
 ,
,
![]() .
.
 ,
,
![]()
 ,
,
![]() .
.
 ,
,
![]() .
.
![]()
![]() ,
,
![]() .
.
При
разложении функций в степенные ряды
бывает удобным использовать разложения
![]() .
.
Пример.Разложить по степеням
![]() функцию
функцию![]() .
.
Если
обозначить
![]() ,
то, используя разложение
,
то, используя разложение![]() ,
получаем:
,
получаем: .
.
Поскольку
разложение
![]() справедливо
для
справедливо
для![]() ,
то
,
то![]() может быть любым действительным числом.
может быть любым действительным числом.
Пример.Разложить по степеням
![]() функцию
функцию![]() .
.
Обозначив
![]() и использовав разложение
и использовав разложение![]() ,
получим
,
получим .
.
Это
разложение справедливо для
![]() ,
поскольку
,
поскольку![]() может быть любым числом.
может быть любым числом.
Ряды Фурье
Рассмотрим функциональные ряды, суммы которых, в отличие от степенных рядов, имеют непустое конечное множество точек разрыва в области задания.
Функция
называется кусочно-непрерывной на
отрезке
![]() ,
если она непрерывна всюду, кроме конечного
числа точек разрыва первого рода. Другими
словами, область ее определения можно
разбить на конечное число частичных
отрезков
,
если она непрерывна всюду, кроме конечного
числа точек разрыва первого рода. Другими
словами, область ее определения можно
разбить на конечное число частичных
отрезков![]()
![]() ,
на каждом из которых:
,
на каждом из которых:
функция
 ограничена и непрерывна во внутренних
точках;
ограничена и непрерывна во внутренних
точках;На концах каждого отрезка существуют конечные односторонние пределы
 ,
,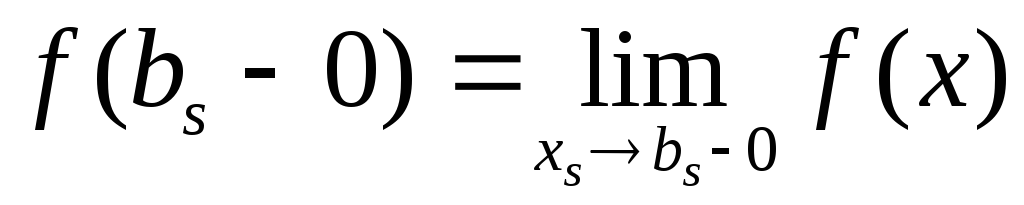
 .
.
Под
интегралом функции
![]() понимается число
понимается число .
.
Можно
доказать, что для кусочно-непрерывной
на отрезке
![]() функции
функции![]() существует обобщенная первообразная
существует обобщенная первообразная (
(![]() ,
,![]() ),
и, следовательно,
),
и, следовательно, .
.
Функция
![]() называетсякусочно-дифференцируемой(иликусочно-гладкой) на
называетсякусочно-дифференцируемой(иликусочно-гладкой) на![]() ,
если производная
,
если производная![]() кусочно-непрерывна на отрезке
кусочно-непрерывна на отрезке![]() .
.
Пусть
функции
![]() и
и![]() кусочно-непрерывны на отрезке
кусочно-непрерывны на отрезке![]() .
Скалярное произведение этих функций
можно определить как
.
Скалярное произведение этих функций
можно определить как .
.
Можно
показать, что произведение двух
кусочно-непрерывных на отрезке
![]() функций есть функция кусочно-непрерывная
на этом отрезке и, следовательно, ее
определенный интеграл на этом отрезке
существует.
функций есть функция кусочно-непрерывная
на этом отрезке и, следовательно, ее
определенный интеграл на этом отрезке
существует.
Тогда
 ,
, .
.
Число
 называетсянормой функции
называетсянормой функции![]() .
.
Очевидны свойства скалярного произведения:
 –свойство
коммутативности или симметрии;
–свойство
коммутативности или симметрии; –свойство
ассоциативности или сочетательности;
–свойство
ассоциативности или сочетательности; ,
причем
,
причем
 .
.
Функции
![]() и
и![]() называютсяортогональными, если
называютсяортогональными, если![]() ,
при этом
,
при этом![]() ,
,![]() .
.
Рассмотрим
основную систему тригонометрических
функций общего периода
![]() :
:
 .
.
Функции
 ,
,![]() и
и ,
,![]() называютсяосновными гармониками.
Их графиками являются синусоиды с
амплитудами соответственно
называютсяосновными гармониками.
Их графиками являются синусоиды с
амплитудами соответственно![]() и
и![]() .
Гармоника
.
Гармоника![]() и поэтому не рассматривается.
и поэтому не рассматривается.
Лемма.Основные тригонометрические функции
попарно ортогональны на любом промежутке,
длина которого равна общему периоду
![]() этих функций, т.е. для стандартного
отрезка
этих функций, т.е. для стандартного
отрезка![]() справедливы условия ортогональности:
справедливы условия ортогональности:
 при
при
 ;
; при
при
 ;
; .
.
Условия ортогональности проверяются непосредственным интегрированием, в ходе которого используются формулы тригонометрии:
 ;
; ;
; .
.
Например,
при
![]() :
:

 ,
,
т.к.
![]() при целых значениях
при целых значениях![]() ;
;

 ;
;




Пусть
![]() – кусочно-непрерывная периодическая
функция периода
– кусочно-непрерывная периодическая
функция периода![]() .
.
Можно
попытаться провести т.н. гармонический
анализ![]() ,
т.е. представить эту функцию в виде суммы
конечного или бесконечного числа
гармоник того же периода
,
т.е. представить эту функцию в виде суммы
конечного или бесконечного числа
гармоник того же периода![]() :
:
 ,
,
![]()
Таким образом, можно прийти к тригонометрическому ряду Фурье:
 .
.
Коэффициент
нулевой гармоники обычно берется с
множителем
![]() .
.
Исторически эта задача впервые возникла при математической обработке результатов наблюдения высоты приливной волны, которая периодически повторяется с течением времени. Гармонический анализ высоты приливной волны позволил дать долгосрочные предсказания ее величины, что было весьма важно для мореплавателей.
Предположим, что ряд:

сходится
на отрезке
![]() и допускает почленное интегрирование,
в результате которого получится
следующее:
и допускает почленное интегрирование,
в результате которого получится
следующее:

Так как из условий ортогональности:

при
![]() ,
то получается
,
то получается .
.
Отсюда:
 .
.
Интересно
отметить, что свободный член
тригонометрического ряда Фурье
 представляет собой среднее значение
периодической функции
представляет собой среднее значение
периодической функции![]() .
.
Если
умножить левую и правую части ряда
 на
на и почленно проинтегрировать, то получится:
и почленно проинтегрировать, то получится:

 .
.
Предварительно, следует отметить, что:

 ,
,
т.е.
 .
.
Отсюда, в силу условий ортогональности, а также с учетом нормировки, получается:
 .
.
Следовательно:
 ,
а значит, заменяя
,
а значит, заменяя![]() на
на![]() (что по смыслу формул допустимо), можно
получить:
(что по смыслу формул допустимо), можно
получить:

Аналогично,
умножая обе части ряда на
 и почленно интегрируя, получим:
и почленно интегрируя, получим:
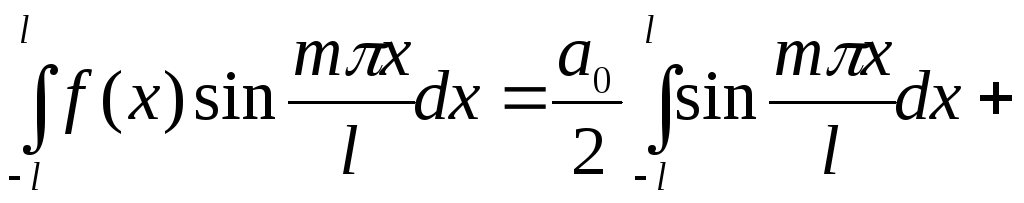
 .
.
В данном случае условие нормировки:
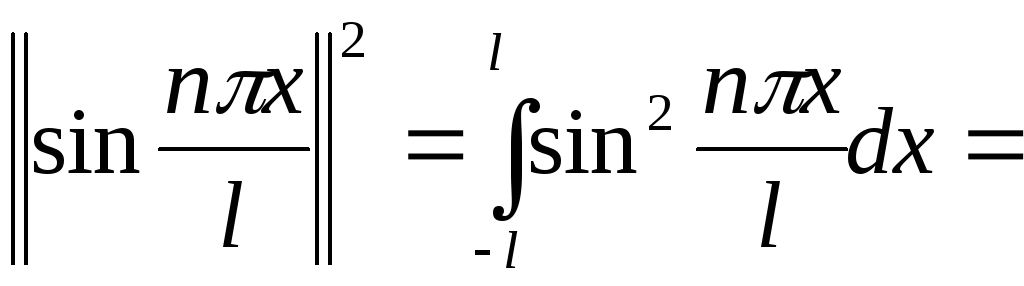
 ,
,
т.е.
 .
.
В силу условий ортогональности:

Следовательно,
 ,
а значит:
,
а значит:
 .
.
Числа
![]() и
и![]()
![]() называютсякоэффициентами Фурьефункции
называютсякоэффициентами Фурьефункции![]() .
.
Тригонометрический ряд:
 ,
,
коэффициентами
которого являются коэффициенты Фурье
данной периодической функции
![]() называется еетригонометрическим
рядом Фурье, независимо от того, будет
ли сумма этого ряда равна функции
называется еетригонометрическим
рядом Фурье, независимо от того, будет
ли сумма этого ряда равна функции![]() или нет. В последнем случае говорят, что
функция
или нет. В последнем случае говорят, что
функция![]() порождает ряд Фурье:
порождает ряд Фурье:
 ,
,
где знак ~ означает «соответствует».
Теорема
сходимости. Пусть периодическая
функция
![]() ,
определенная на
,
определенная на![]() ,
кроме, может быть, точек ее разрывов, и
имеющая период
,
кроме, может быть, точек ее разрывов, и
имеющая период![]() ,
является кусочно–дифференцируемой
(или кусочно–гладкой) на любом промежутке,
длина которого равна периоду этой
функции.
,
является кусочно–дифференцируемой
(или кусочно–гладкой) на любом промежутке,
длина которого равна периоду этой
функции.
Тогда:
Ее тригонометрический ряд Фурье сходится для любого значения
 ,
т.е. существует сумма ряда Фурье
,
т.е. существует сумма ряда Фурье
 ;
;
Сумма ряда Фурье
 равна функции
равна функции в точках
в точках ее непрерывности
ее непрерывности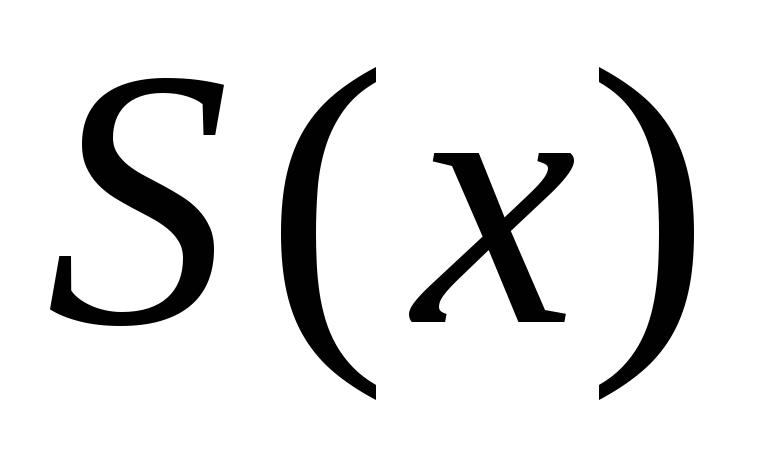 =
= и равна среднему арифметическому
пределов функции
и равна среднему арифметическому
пределов функции слева и справа в точках
слева и справа в точках разрыва функции, т.е.:
разрыва функции, т.е.:

Поскольку,
для точек непрерывности
![]() функции
функции![]() можно записать
можно записать![]() ,
то в общем случае:
,
то в общем случае:
 .
.
Таким
образом, для тригонометрического ряда
Фурье функции
![]() имеем:
имеем:
 ,
,
где
коэффициенты
![]() и
и![]() определяются по формулам:
определяются по формулам:

 .
.
Если
принять, что период функции
![]() равен
равен![]() ,
т.е.
,
т.е.![]() ,
то расчетные формулы значительно
упрощаются:
,
то расчетные формулы значительно
упрощаются:



где
![]() .
.

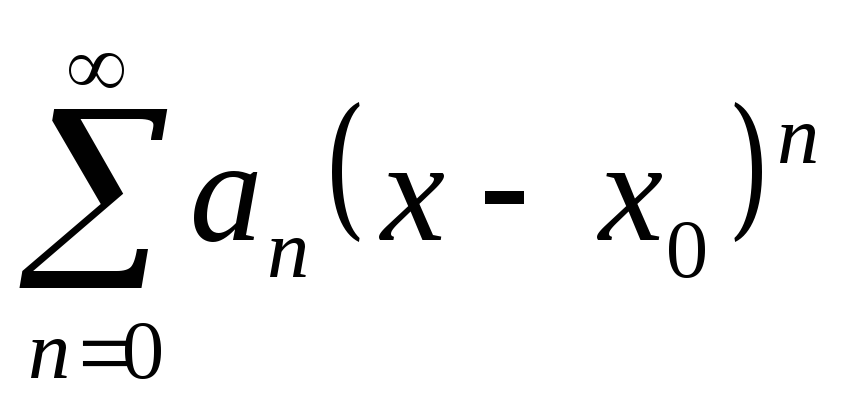 ,
,



