
- •Академия управления при Президенте Республики Беларусь
- •Содержание
- •Тема 4. Функции 9
- •Тема 5. Дифференциальное исчисление функций одной переменной 34
- •Тема 6. Исследование функций 45
- •Тема 7. Пространство 66
- •Тема 8. Неопределенные интегралы 100
- •Тема 9. Определенные интегралы 114
- •Тема 10. Понятие кратного интеграла 132
- •Тема 11. Ряды 140
- •Тема 12. Дифференциальные уравнения 171
- •Тема 4. Функции Лекция 15. Функции
- •Основные понятия
- •Понятие числовой последовательности
- •Сходящиеся последовательности
- •Бесконечный предел
- •Замечательные пределы
- •Принцип сходимости
- •Предел функции. Теорема Гейне
- •Односторонние пределы
- •Пределы на бесконечности
- •Бесконечные пределы
- •Непрерывность функции
- •Непрерывность композиции
- •Точки разрыва
- •Контрольные вопросы к теме №4
- •Тема 5. Дифференциальное исчисление функций одной переменной Лекция 16. Дифференциальное исчисление функций одной переменной
- •Определение и смысл производной
- •Построение касательной к графику функции
- •Экономический смысл производной
- •Эластичность функции
- •Дифференцируемость функции
- •Правила дифференцирования
- •Производная сложной функции
- •Производная обратной функции
- •Дифференциал
- •Приближенные вычисления
- •Свойства дифференцируемых функций
- •Правила Лопиталя
- •Монотонность функции
- •Локальный экстремум
- •Исследование стационарных точек
- •Глобальный экстремум
- •Выпуклость и перегибы графика функции
- •Исследование функции и построение графика
- •Интерполяция и аппроксимация функций
- •Интерполяционный полином Лагранжа
- •Формула Тейлора
- •Основные разложения
- •Понятие об эмпирических формулах
- •Контрольные вопросы к теме №6
- •Тема 7. Пространство Лекция 18. Пространство
- •Точки, расстояние. Множества в
- •Последовательности в. Сходимость
- •Функции в. Предел. Теорема Гейне
- •Непрерывность функции в
- •Непрерывность на множестве
- •Теоремы о непрерывности
- •Дифференцируемость функций в. Частные производные
- •Дифференциал функции нескольких переменных
- •Необходимые условия дифференцируемости. Достаточные условия
- •Дифференцирование функции, заданной неявно и композиции функций
- •Полные дифференциалы и частные производные высших порядков. Признак полного дифференциала
- •Формула Тейлора
- •Локальный экстремум функции нескольких переменных. Необходимое и достаточное условия. Исследование стационарных точек
- •Условный экстремум функций нескольких переменных. Глобальный экстремум
- •Метод наименьших квадратов
- •Контрольные вопросы к теме №7
- •Свойства неопределенного интеграла
- •Замена переменных
- •Интегрирование по частям
- •Интегрирование рациональных функций. Метод рационализации
- •Вычисление
- •Вычисление
- •Вычисление
- •Вычисление
- •Контрольные вопросы к теме №8
- •Тема 9. Определенные интегралы Лекция 20. Определенные интегралы
- •Интегральные суммы
- •Необходимое и достаточное условие интегрируемости
- •Равномерно непрерывные функции
- •Интегрируемость непрерывных, разрывных и монотонных функций
- •Основные свойства определенного интеграла
- •Оценки интегралов. Формулы среднего значения
- •Основные правила интегрирования
- •Приложения определенного интеграла Площадь плоской фигуры
- •. Объемы тел вращения
- •Несобственные интегралы
- •Интегрирование неограниченных функций
- •Интегрирование по бесконечному промежутку
- •Приближенное вычисление определенных интегралов
- •Формула прямоугольников
- •Формула трапеций
- •Контрольные вопросы к теме №9
- •Тема 10. Понятие кратного интеграла Лекция 21. Понятие кратного интеграла
- •Интегрирование функций многих переменных
- •Свойствакратного интеграла
- •Контрольные вопросы к теме №10
- •Тема 11. Ряды Лекция 22. Ряды
- •Основные понятия
- •Положительные ряды
- •Знакочередующиеся ряды
- •Абсолютная сходимость
- •Функциональные ряды
- •Степенной ряд
- •Ряды Фурье
- •Ряды Фурье четных и нечетных функций
- •Понятие о рядах Фурье непериодических функций
- •Контрольные вопросы к теме №11
- •Тема 12. Дифференциальные уравнения Лекция 23. Дифференциальные уравнения
- •Основные понятия
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения семейства кривых
- •Геометрическое истолкование дифференциального уравнения
- •Задача Коши
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные дифференциальные уравнения
- •Метод Эйлера приближенного решения дифференциальных уравнений
- •Дифференциальные уравнения второго порядка
- •Задача Коши
- •Интегрируемые типы дифференциальных уравнений второго порядка
- •Случаи понижения порядка
- •Общие свойства решений линейных однородных дифференциальных уравнений второго порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
- •Линейные дифференциальные уравнения-го порядка
- •Контрольные вопросы к теме №12
- •Вопросы к экзамену
- •Литература
- •Высшая математика
- •220007, Г. Минск, ул. Московская, 17.
Дифференциальные уравнения второго порядка
Общий вид дифференциального уравнения второго порядка, разрешенного относительно старшей производной
![]() .
.
Общее
решение
![]() этого уравнения содержит две независимые
произвольные постоянные
этого уравнения содержит две независимые
произвольные постоянные![]() и
и![]() .
Геометрически общее решение представляет
собой бесконечную совокупность
интегральных кривых, зависящую от двух
независимых параметров
.
Геометрически общее решение представляет
собой бесконечную совокупность
интегральных кривых, зависящую от двух
независимых параметров![]() и
и![]() .
Вообще говоря, через каждую точку
.
Вообще говоря, через каждую точку![]() плоскости
плоскости![]() проходит пучок интегральных кривых.
Поэтому, чтобы из семейства интегральных
кривых выделить одну определенную
интегральную кривую, недостаточно
указать точку
проходит пучок интегральных кривых.
Поэтому, чтобы из семейства интегральных
кривых выделить одну определенную
интегральную кривую, недостаточно
указать точку![]() ,
через которую проходит эта кривая, нужно
указать еще и направление, в котором
кривая проходит через эту точку, т.е.
задать тангенс угла наклона касательной
к этой кривой в точке
,
через которую проходит эта кривая, нужно
указать еще и направление, в котором
кривая проходит через эту точку, т.е.
задать тангенс угла наклона касательной
к этой кривой в точке![]() с положительным направлением оси
с положительным направлением оси![]() .
.
Задача Коши
Задача
нахождения решения дифференциального
уравнения, удовлетворяющего условиям:
![]() ,
где
,
где![]() ‑ заданные числа, называетсязадачей
Коши. Эти условия часто называют
начальными условиями, так как с
экономической точки зрения они означают,
что в фиксированный момент времени
задано начальное состояние экономического
процесса и скорость его изменения.
‑ заданные числа, называетсязадачей
Коши. Эти условия часто называют
начальными условиями, так как с
экономической точки зрения они означают,
что в фиксированный момент времени
задано начальное состояние экономического
процесса и скорость его изменения.
Геометрический смысл задачи Коши состоит в нахождении интегральной кривой, проходящей через заданную точку и имеющей заданный угловой коэффициент касательной в этой точке.
Пример.Решить задачу Коши
![]() .
.
Найдем
все решения данного уравнения. Интегрируем:
![]() ,
,![]() .
.
Воспользовавшись
начальными условиями, определим значение
констант
![]() и
и![]() из системы уравнений:
из системы уравнений: .
.
Следовательно,
![]() ,
,![]() и искомое решение:
и искомое решение:![]() .
.
Интегрируемые типы дифференциальных уравнений второго порядка
В общем случае дифференциальное уравнение второго порядка не решается аналитически, однако, в некоторых случаях, дифференциальные уравнения второго порядка определенных типов решаются с применением операции неопределенного интегрирования.
Тип
I.
![]()
Интегрируя,
получим
![]() .
.
Интегрируя
еще раз, окончательно получим
![]() ,
где
,
где![]() и
и![]() – произвольные постоянные, и неопределенные
интегралы трактуются как некоторые
первообразные соответствующих функций.
– произвольные постоянные, и неопределенные
интегралы трактуются как некоторые
первообразные соответствующих функций.
Тип
II.
![]() .
.
Положим,
![]() .
Отсюда, рассматривая
.
Отсюда, рассматривая![]() как функцию от
как функцию от![]() ,
будем иметь:
,
будем иметь:![]() .
.
Следовательно,
уравнение
![]() примет вид
примет вид![]() .
Разделяя переменные, получим
.
Разделяя переменные, получим![]() .
.
Интегрируя последнее уравнение, находим:
![]() или
или
![]() .
.
Так
как
 ,
то
,
то .
Отсюда, разделяя еще раз переменные и
интегрируя, получим:
.
Отсюда, разделяя еще раз переменные и
интегрируя, получим:
 .
.
Тип
III.
![]() .
.
Положим
![]() ,
тогда
,
тогда .
Уравнение
.
Уравнение
![]() примет вид:
примет вид:

Разделяя переменные и интегрируя, получим:


Определив
из этого уравнения величину
 ,
путем вторичного интегрирования, можно
найти и
,
путем вторичного интегрирования, можно
найти и![]() .
.
Случаи понижения порядка
Укажем
два случая, когда дифференциальное
уравнение второго порядка
![]() приводится к дифференциальному уравнению
первого порядка.
приводится к дифференциальному уравнению
первого порядка.
I.Пусть левая часть уравнения не содержит![]() ,
т.е. уравнение имеет вид
,
т.е. уравнение имеет вид![]() .
Полагая
.
Полагая![]() и
и![]() ,
получим дифференциальное уравнение
первого порядка
,
получим дифференциальное уравнение
первого порядка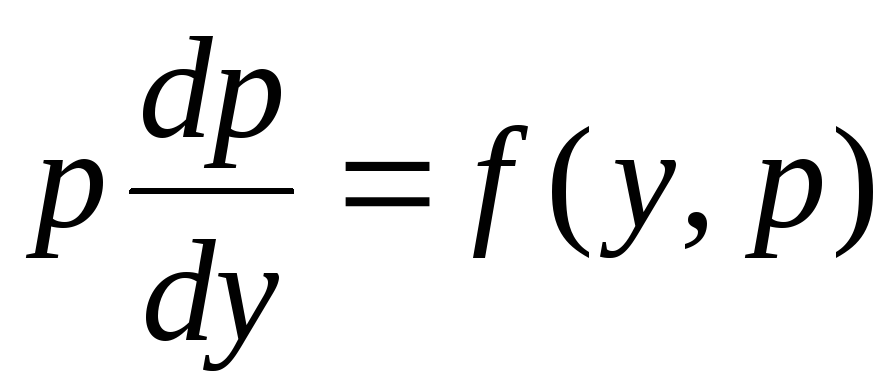 ,
где роль независимой переменной играет
,
где роль независимой переменной играет![]() .
.
II.Пусть левая часть уравнения не содержит![]() ,
т.е. уравнение имеет вид
,
т.е. уравнение имеет вид![]() .
Полагая
.
Полагая![]() и
и ,
получим уравнение первого порядка
,
получим уравнение первого порядка с неизвестной функцией
с неизвестной функцией![]() .
.
Общие свойства решений линейных однородных дифференциальных уравнений второго порядка
Рассмотрим
линейное однородное дифференциальное
уравнение второго порядка
![]() с непрерывными коэффициентами
с непрерывными коэффициентами![]() и
и![]() .
.
Предположим,
что
![]() и
и![]() – частные (т.е. не содержащие произвольных
постоянных) решения этого уравнения.
– частные (т.е. не содержащие произвольных
постоянных) решения этого уравнения.
Определение.Два решения
![]() и
и![]() называютсялинейно зависимыми,
если можно подобрать числа
называютсялинейно зависимыми,
если можно подобрать числа
![]() и
и![]() не равные одновременно нулю, такие, что
линейная комбинация этих функций
тождественно равна нулю, т.е.
не равные одновременно нулю, такие, что
линейная комбинация этих функций
тождественно равна нулю, т.е.![]() .
.
В
противном случае, если таких чисел
подобрать нельзя, решения
![]() и
и![]() называютсялинейно независимыми.
Иными словами, если функции
называютсялинейно независимыми.
Иными словами, если функции![]() и
и![]() линейно независимы и выполняется
тождество
линейно независимы и выполняется
тождество![]() ,
то числа
,
то числа![]() и
и![]() одновременно равны нулю.
одновременно равны нулю.
Очевидно,
решения
![]() и
и![]() будут линейно зависимыми тогда и только
тогда, когда они пропорциональны друг
другу, т.е.
будут линейно зависимыми тогда и только
тогда, когда они пропорциональны друг
другу, т.е.![]()
![]() (или наоборот), где
(или наоборот), где![]() – постоянный коэффициент пропорциональности.
– постоянный коэффициент пропорциональности.
Понятие линейной независимости применимо к любой паре функций. Аналогично определяется линейная зависимость и линейная независимость нескольких функций.
Зная два частных линейно независимых решения линейного однородного уравнения, легко получить общее решение этого уравнения.
Теорема.
Если
![]() и
и![]() – линейно независимые частные решения
линейного однородного дифференциального
уравнения второго порядка
– линейно независимые частные решения
линейного однородного дифференциального
уравнения второго порядка![]() ,
то общее решение уравнения есть линейная
комбинация этих частных решений, т.е.
общее решение имеет вид
,
то общее решение уравнения есть линейная
комбинация этих частных решений, т.е.
общее решение имеет вид![]() ,
где
,
где![]() и
и![]() – произвольные конечные постоянные
величины.
– произвольные конечные постоянные
величины.
